素因数分解とは、自然数を素因数の積の形に表すこと。
なのですが、
これだけの説明では「どういうこと!?」って感じですよね(^^;)
というわけで、今回の記事では素因数分解についてイチから解説していきます。
今回の記事は、こちらの動画でも解説しています(/・ω・)/
素因数分解とは
ある整数を自然数のかけ算(積)の形で表したとき
それぞれの自然数のことを因数(いんすう)といいます。
さらに、素数である因数のことを素因数(そいんすう)といいます。
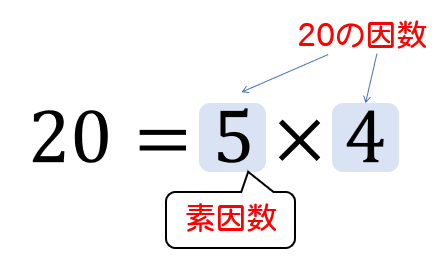
このとき、5と4は20の因数であり、5は素数でもあるので素因数となります。
4は素数ではないので、因数ではあるけど素因数ではありませんね。
素数とは、1とその数自身でしか割り切ることができない数のこと。
【例】\(2, \ 3, \ 5, \ 7, \ 11, \ 13, \cdots\)
ただし、1は素数ではないので注意!
そして、素因数ではない4というのは、
次のように素数を使って、さらに細かく積の形で表すことができます。
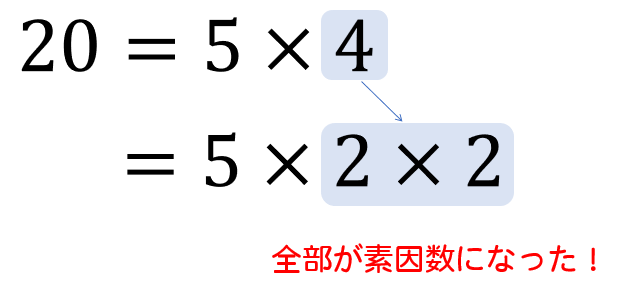
すると、20を5と2の素因数だけの積で表すことができました。
このように、自然数を素因数だけの積になるまで細かくわけていくこと。
これを素因数分解といいます。
同じ素因数がある場合には、

このように指数を使ってコンパクトにまとめておきましょう。
\(5\times 2^2\) ではなく、\(2^2\times 5\) のように素因数を小さい順に並べていくのが一般的です。
素因数分解のやり方
素因数分解は、逆割り算のような形でやると便利です。
次の例題を使って、素因数分解のやり方を確認していきましょう!
【例題】
60を素因数分解しなさい。
まずは、60を割り切ることができる素数で割ります。
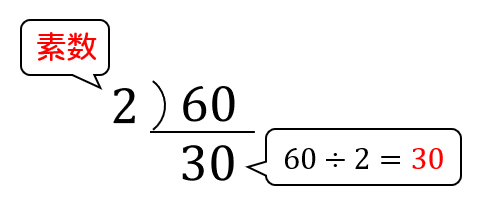
次に、30を素数で割る。
これを最後が素数になるまで繰り返していきます。
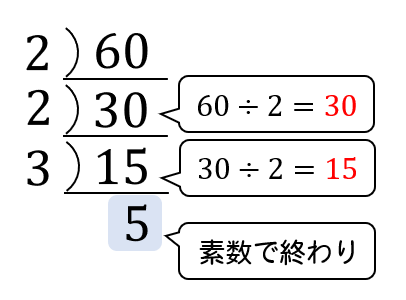
ここまできたら、素数部分を取り出していきます。
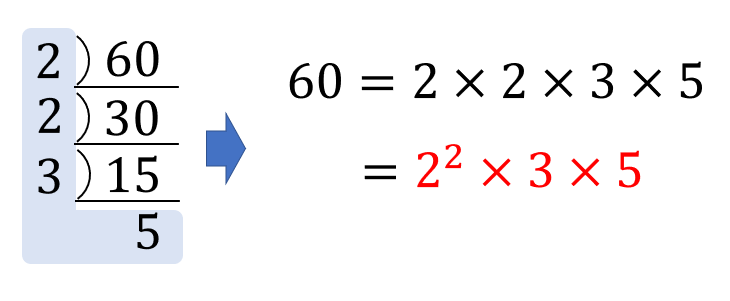
すると、素因数分解の完成ですね!
慣れてくるとすごくラクになるので、この逆割り算のやり方を練習しておきましょう!
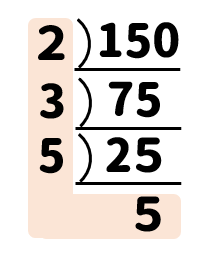
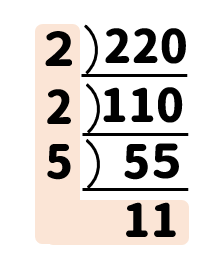
【練習問題】
次の数を素因数分解しなさい。
(1)150
(2)220

まとめ!
お疲れさまでした!
素因数分解のやり方はバッチリかな?
やり方をマスターした人は、こちらの記事で素因数分解を使った応用問題にも挑戦してみてくださいね!


















コメントを残す