ユークリッド互除法のやり方！最大公約数を求める手順をイチから解説！

高校数学Aで学習する整数の性質の単元から

「ユークリッドの互除法のやり方」

についてイチから解説していきます。

 

この記事を通して、互除法のやり方をマスターして、

スラスラと最大公約数が求めれるようになりましょう！

 

今回の内容をサクッと理解したい方はこちらをどうぞ！

ユークリッドの互除法とは

自然数 \(a, \ b\) について、\(a\) を \(b\) で割ったときの余りを \(r\) とすると、

\(a\) と \(b\) の最大公約数は、\(b\) と \(r\) の最大公約数に等しい。

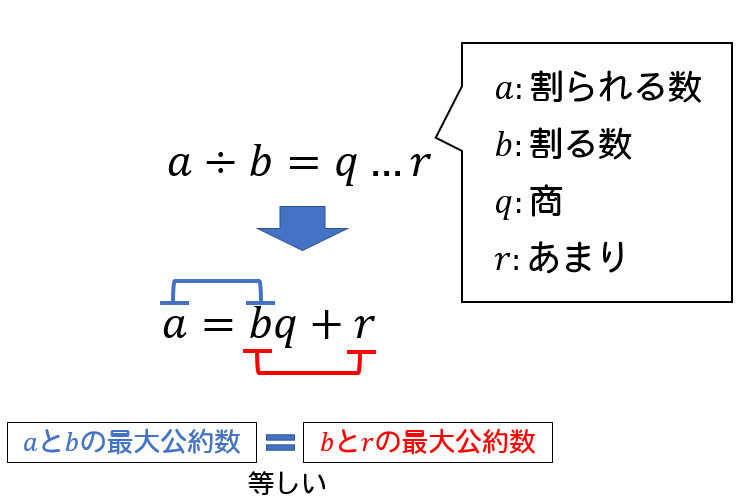
という性質があります。

これを利用して、最大公約数を求める方法のことをユークリッドの互除法、または互除法といいます。

 

例えば、629と259の最大公約数を求める場合。

>最大公約数、最小公倍数の求め方と性質をイチから解説！

ここで学習した通り、素因数分解を利用して考えることもできるのですが、

629，259ともに素因数分解をするのが難しいですよね(^^;)

割れる数を探すのに一苦労です…

 

そんなときに役に立つのが互除法を使ったやり方になります。

次の章で、互除法のやり方について確認していきましょう。

ユークリッドの互除法のやり方

まず、\(629 \div 259\) を計算しましょう。

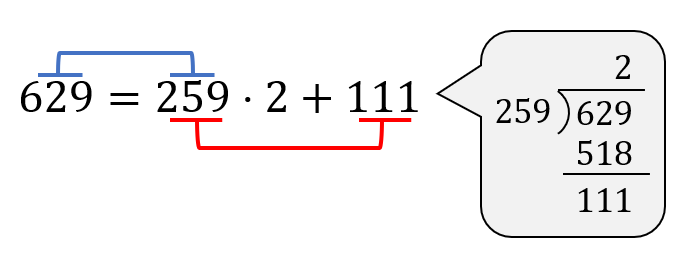
すると、「629と259の最大公約数」と「259と111の最大公約数」が等しいことが分かります。

 

次に、\(259 \div 111\) を計算しましょう。

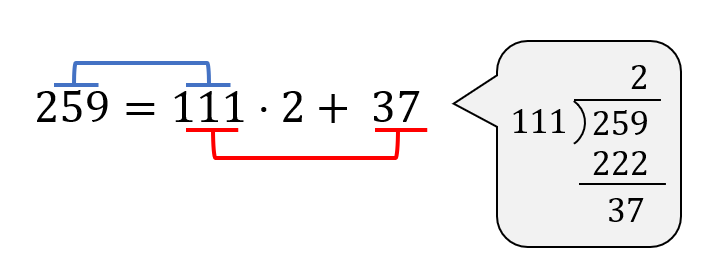
すると、「259と111の最大公約数」と「111と37の最大公約数」が等しいことが分かります。

 

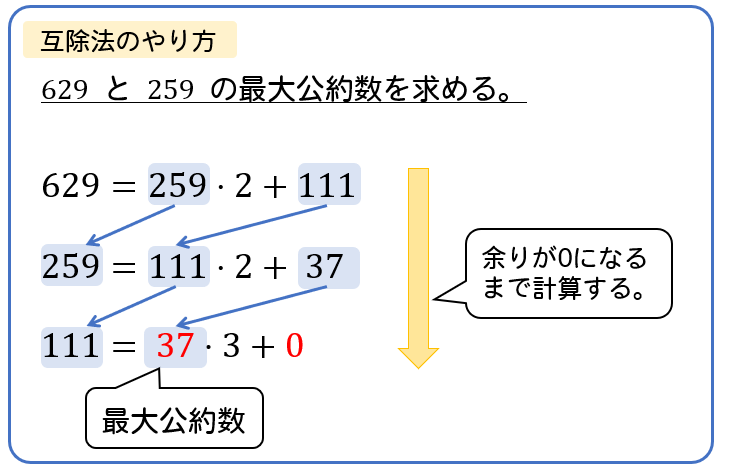
さらに繰り返し計算していきます。\(111 \div 37\) を計算しましょう。

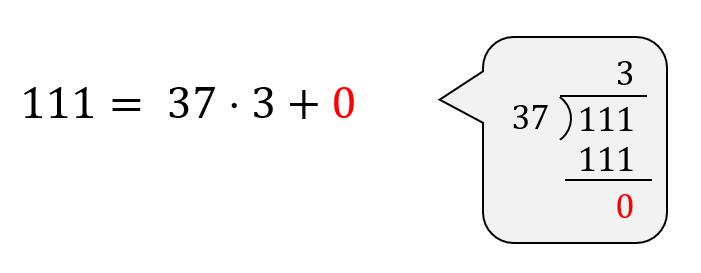
すると、余りが0になりました。

このように余りが0になるまで割り算を続けていきます。

余りが0になった（割り切れた）ことから、111と37の最大公約数は37であることが分かります。

 

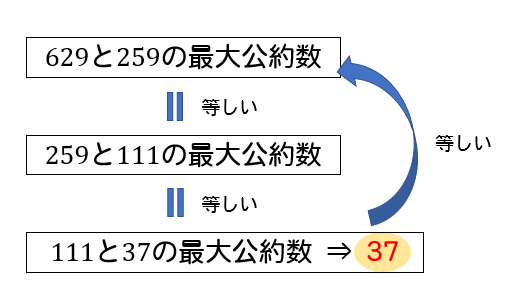
つまり、このように629と259の最大公約数も37になるってことが分かりました。

 

大きい数どうしの最大公約数は見つけにくいものですが、

これを小さな数に変換していくことによって、最大公約数を見つけやすくしてるんですね！

 

互除法の筆算のやり方

こちらの章では、互除法の筆算のやり方について紹介しておきます。

さっきと同じ問題を、今度は筆算を用いたやり方で求めてみましょう。

 

まずは、\(629\div 259\) を筆算で計算します。

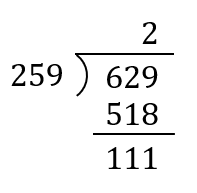
次に、余りを割る数の左に持ってきて、\(259\div 111\) を計算します。

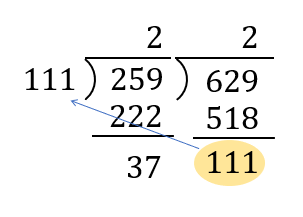
これを繰り返し、余りが0になるまで計算します。

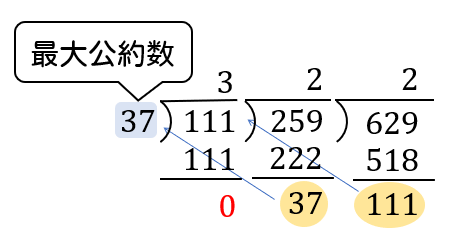
余りが0になったとき、一番左にある数（割る数）が最大公約数となります。

 

以上が筆算を使ったやり方です。

結局やっている計算は同じことなのですが、

割り算をするときに暗算が難しく、筆算を利用する必要があるのであれば、

今回紹介したように、筆算を並べていくやり方でやっていくと式を書き並べる手間が省けて、ちょっとだけ時短になりますね。

互除法の練習！

 

まとめ！

これでユークリッドの互除法のやり方はバッチリかな？？

次に学習する「一次不定方式」の内容で、

互除法が、すっごく役に立つことになります。

なので、今のうちにしっかりと使えるように練習しておきましょう！