今回は中2で学習する『式の計算』の単元から
単項式、多項式がそれぞれ何次式になるのか？
係数や次数ってなに？
という問題について解説していきます。
今回の記事は、こちらの動画でも解説しています(/・ω・)/
単項式の次数
数や文字についての乗法だけでできている式を単項式といいます。
$$3x, -4ab, 2a^5, -\frac{2}{3}$$
このように項が１つしかない式が単項式ですね。
そして
文字の項で、文字にかけてある数の部分を係数
かけあわされている文字の個数を、その式の次数といいます。
また、次数が2の式を2次式といいます。
同様に次数が3であれば3次式、４であれば4次式というように
その式が何次式であるかを判断します。
つまり、式の次数を調べれば何次式になるかがわかるということです。
それでは、次の単項式の係数、次数、何次式？について考えてみましょう。
$$\LARGE{4a^2b}$$
係数：４ 次数：３ 3次式
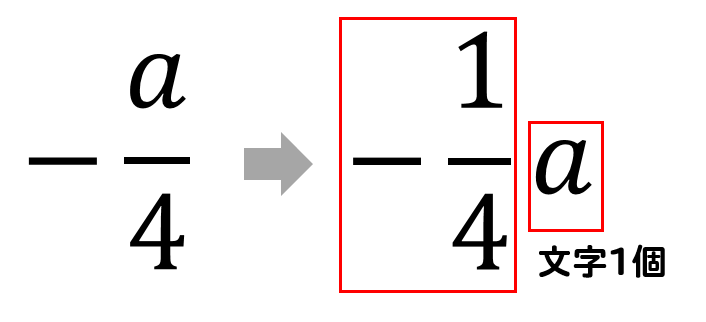
$$\LARGE{-\frac{a}{4}}$$
係数：\(\displaystyle -\frac{1}{4}\) 次数：1 1次式
分子に文字があると分かりにくいという場合には、上の式のように文字を横に書いて表してみると分かりやすくなりますね！
間違っても係数を\(-4\)とはしないでくださいね。
多くの人が陥ってしまうミスなので気をつけてください！
多項式の次数
単項式の和の形で表された式を多項式といいます。
$$2a-b, x^2+3x+4, 2xy^3-4x$$
このように項が複数ある式が多項式ですね。
多項式の次数を考える場合には
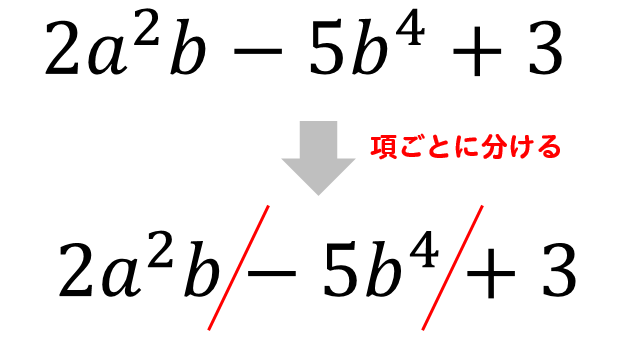
そして、各項の次数のうち、1番大きいものを、その式の次数とします。
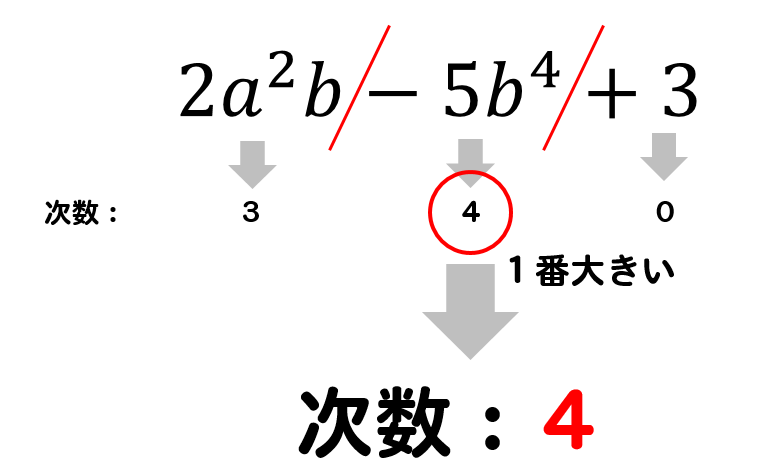
このように多項式の次数を求める場合には
まずは、式を項ごとに分けて
それぞれの次数の中から1番大きい数字を、その多項式の次数とします。
それでは、次の多項式の問題について考えてみましょう。
$$\LARGE{x^2+4x-5}$$
項：\(x^2, 4x, -5\)
係数：\(1, 4\)
次数：2
2次式
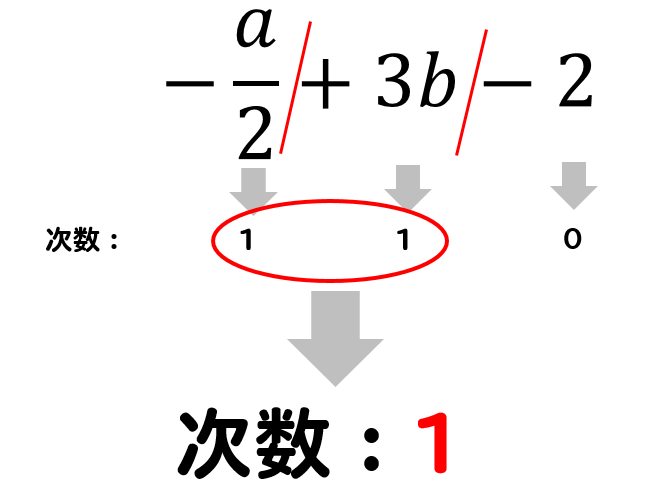
$$\LARGE{-\frac{a}{2}+3b-2}$$
項：\(\displaystyle -\frac{a}{2}, 3b, -2\)
係数：\(\displaystyle -\frac{1}{2}, 3\)
次数：1
1次式
練習問題に挑戦！
下のア～カの式について、次の問いに答えなさい。
ア \(2x+3y\) イ \(-mn\) ウ \(a^2-a+6\)
エ \(5a^2b\) オ \(8\) カ \(\displaystyle \frac{x^3}{2}+4xy-y^2\)
（1）単項式と多項式に分け、記号で答えなさい。
（2）ウの式の項と係数を答えなさい。
（3）2次式をすべて選び記号で答えなさい。
まとめ
お疲れ様でした！
次数や係数については、これでバッチリですね(^^)
単項式と多項式では次数の求め方がちょっと違ったので
それぞれの求め方について、しっかりと覚えておきましょう！
単項式の場合 ⇒ かけあわされている文字の個数が次数
多項式の場合 ⇒ 各項の次数の中から一番大きい数が、その式の次数
数スタのオリジナル教材を販売中！
数スタのオリジナル教材を作成しました。
第1弾は高校入試対策、規則性の教材です。
苦手にしている人が多い単元ですが、
コツを掴むと簡単に解けるようになります。
⇒ 【高校入試】規則性の問題をゼロから＋10点する教材
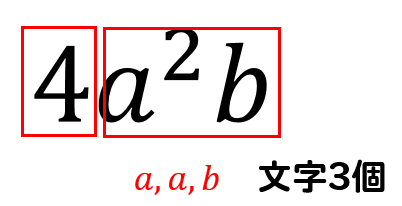
コメント失礼します。
2次式、3次式、4字式と記載されておりましたが、正しくは 【二次式】【三次式】
【四次式】と表記するのではないでしょうか？
以前、恩師に 何故漢字を使用するのか、『三角形を“3角形”と表記しないのと同じ』と教えて頂いたことがありますので…
＞また、次数が2の式を2次式といいます。
同様に次数が3であれば3次式、４であれば4次式というように
コメントありがとうございます。
記事作成にあたって参考にさせていただいた「東京書籍」さんの文献では1次式、2次式…という表記になっておりました。
私個人としては、1次式、一次式の表記はどちらでもよいものかと思っておりましたが、その判断に自信はありません(^^;)
明確な答えにならず申し訳ありません…