今回の記事では、高校数学Ⅰで学習する
正弦定理
についてまとめていきます。
正弦定理ってどんな公式?
公式の証明は?
正弦定理を使った問題の解き方は?
という点についてお話を進めていきます。
正弦定理を使った問題って…
分数の計算が複雑!!
なので、この記事では正弦定理を使って計算する場合の途中式なども丁寧に解説していきますね(^^)
正弦定理を使った基本問題の解き方はこちらの動画でも解説しています(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
正弦定理の公式
△ABCの外接円の半径を\(R\)とするとき
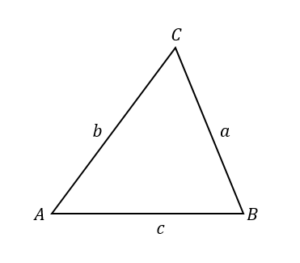
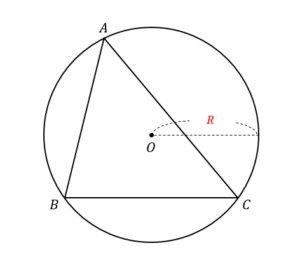
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$
また、上の式を変形して
$$b=2R\sin B$$
$$c=2R\sin C$$
この形で使うこともあります。
正弦定理って外接円の半径を使って式を作ってるけど
そもそも、三角形ってどんな形でも外接円があるの??
って疑問を抱いた方はおられませんか。
そんなの当たり前だろ!っ方は話を流してくださいw
当時、学生だった僕はとっても疑問に思ってました(^^;)
だけど、この記事にあることを理解すればどんな三角形にも外接円があることが分かりますね。
正弦定理の公式証明
なぜ正弦定理が成り立つのか。
これを証明するためには、∠Aが鋭角、直角、鈍角の場合でそれぞれ考えていきましょう。
鋭角の場合
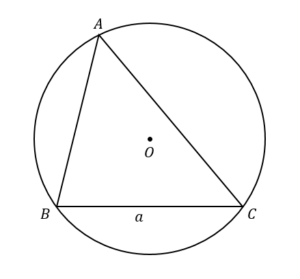
∠Aが鋭角の場合、\(\frac{a}{\sin A}=2R\) となることを証明します。
まずは、外接円の中心を通るよう次のような三角形を作ります。
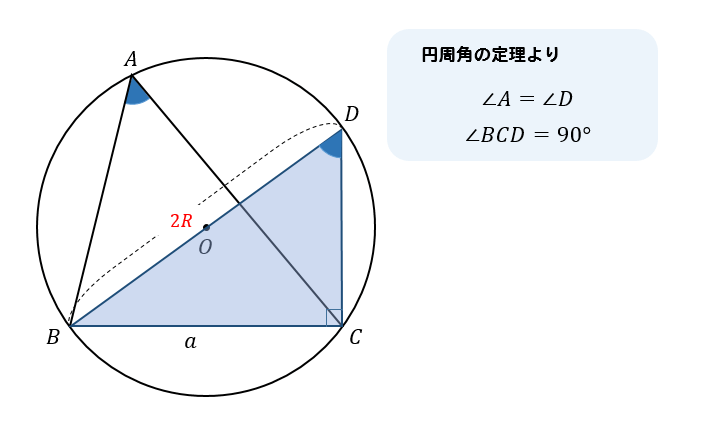
すると、辺BDは外接円の直径となっているため、\(BD=2R\) と表せます。
さらに、円周角の定理より
$$∠A=∠D, ∠BCD=90°$$
となります。
ここで、△BCDの直角三角形に注目すると
$$\begin{eqnarray}2R\cdot \sin D&=& a\\[5pt]2R\sin A&=&a\\[5pt]\frac{a}{\sin A}&=&2R\end{eqnarray}$$
このように正弦定理の式を導くことができます。
同様に考えれば
$$\frac{b}{\sin B}=2R$$
$$\frac{c}{\sin C}=2R$$
となるので
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$
直角の場合
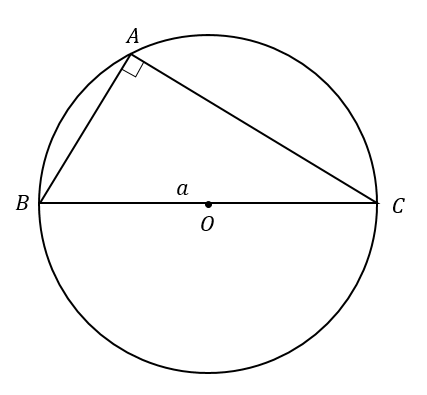
∠Aが直角の場合、\(\frac{a}{\sin A}=2R\) となることを証明します。
∠Aが直角の場合には、辺BCが外接円の直径となっていることが分かります。
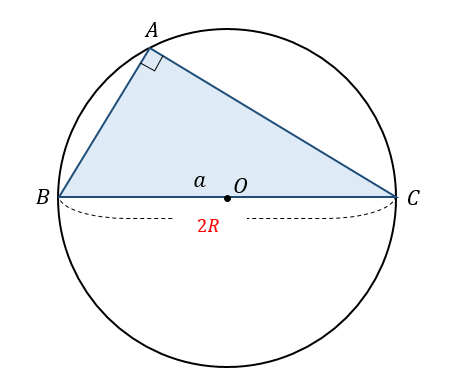
さらに、\(\sin A=\sin 90°=1\) であることを考えると
$$\begin{eqnarray}a&=&2R\\[5pt]a&=&2R\cdot \sin 90°\\[5pt]a&=&2R\sin A \\[5pt]\frac{a}{\sin A}&=&2R\end{eqnarray}$$
同様に考えれば
$$\frac{b}{\sin B}=2R$$
$$\frac{c}{\sin C}=2R$$
となるので
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$
鈍角の場合
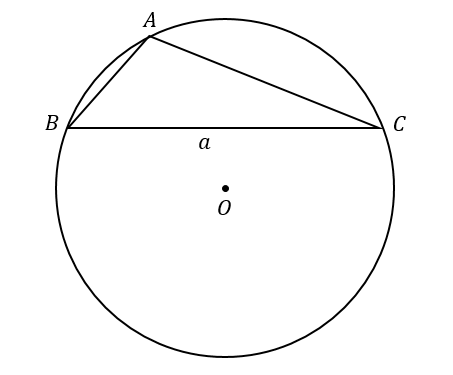
∠Aが鈍角の場合、\(\frac{a}{\sin A}=2R\) となることを証明します。
まずは、外接円の中心を通るよう次のような三角形を作ります。
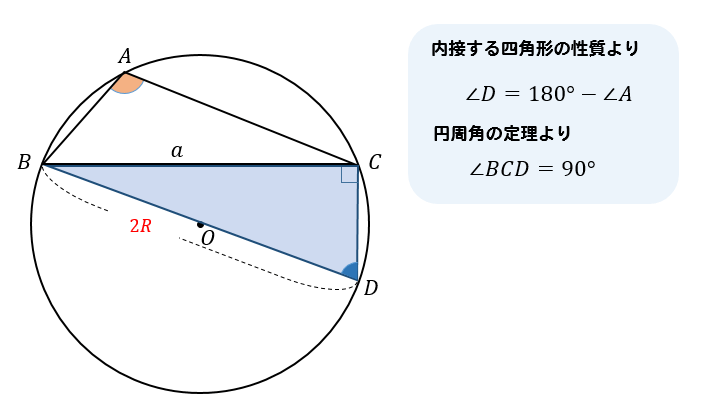
すると、四角形ABDCは円に内接しているので、\(∠A+∠D=180°\)となります。
このことから
$$\sin D=\sin (180°-A)=\sin A$$
さらに、円周角の定理より、\(∠BCD=90°\) となるので△BDCは直角三角形になる。
以上より、△BDCに注目すると
$$\begin{eqnarray}a&=& 2R\cdot \sin D\\[5pt]a&=&2R\sin A\\[5pt]\frac{a}{\sin A}&=&2R \end{eqnarray}$$
同様に考えれば
$$\frac{b}{\sin B}=2R$$
$$\frac{c}{\sin C}=2R$$
となるので
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$
以上が正弦定理の証明でした。
証明を問題として問われることが少ないと思いますが、頭の片隅に出も入れといてもらえると知識の幅が広がって数学の力がついてくるはずです(^^)
それでは、次では正弦定理の覚え方、余弦定理との使い分けについて見ていきましょう。
正弦定理の覚え方、余弦定理との使い分け
正弦定理と余弦定理
2つの定理があって、どっちを使えばよいのか分からん!
そんな困った場面に出くわすことがあるでしょう。
そういうときの見極め方として、覚えておいてもらいたいことがあります。
正弦定理は向かい合う角と辺、外接円
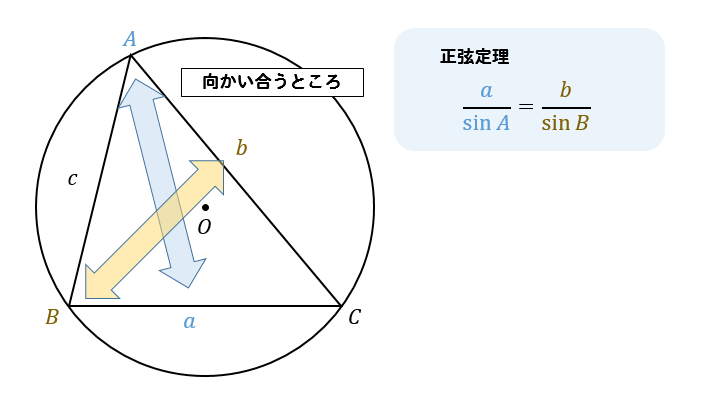
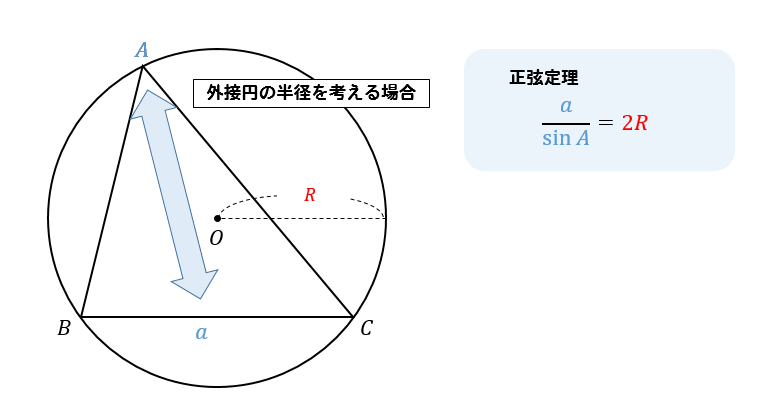
このように、向かい合う辺と角や外接円の半径について考える場合には正弦定理を使いましょう。
一方、余弦定理は矢印型
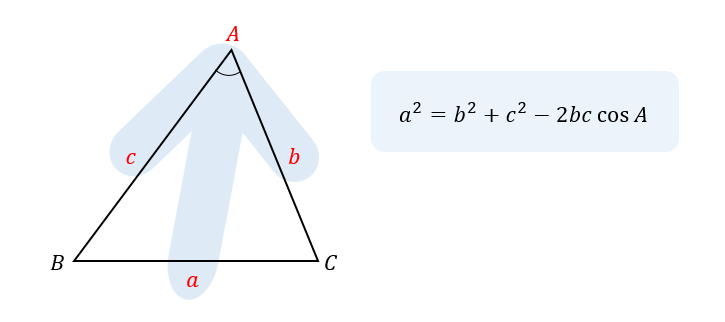
このように矢印型に位置している辺、角を考える場合には余弦定理を使うといいでしょう。
正弦定理の問題の解き方
では、ここから正弦定理を使った問題の解き方について確認していきましょう。
正弦定理を使った問題は、分数の計算が複雑!
分数分の分数…なんていう形も当たり前にできてきます。
分数の中に分数がある形の計算方法については
>【分数分の分数?】分母と分子(上と下)に分数があるときのやり方を解説!
こちらの記事でも解説しているので、計算に不安がある方はチェックしておいてください。
【正弦定理の問題】辺の大きさを求める①
△ABCにおいて、次のものを求めよ。
$$a=6, A=45°, B=60°のとき、b$$
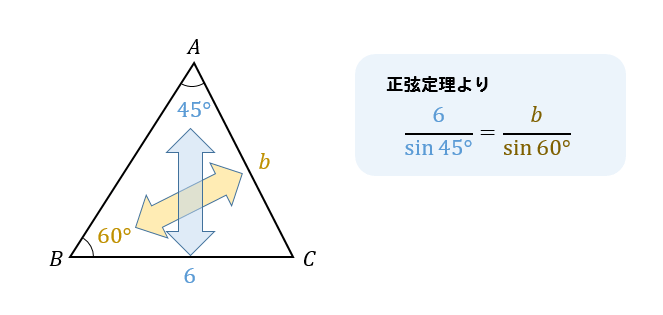
このように、向かい合う辺と角どうしを使って正弦定理から式を作ります。
辺の大きさを求めたい場合には
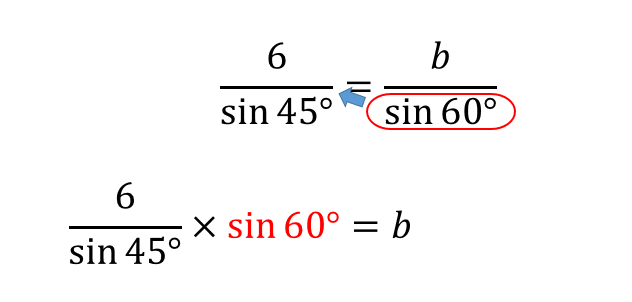
このように式変形してから計算していくとよいです。
$$\begin{eqnarray}\frac{6}{\sin 45°}&=&\frac{b}{\sin 60°}\\[5pt]\frac{6}{\sin 45°}\times \sin 60°&=&b\\[5pt]\frac{6}{\frac{1}{\sqrt{2}}}\times \frac{\sqrt{3}}{2}&=&b\\[5pt]6\times \frac{\sqrt{2}}{1}\times \frac{\sqrt{3}}{2}&=&b \\[5pt]b&=&3\sqrt{6} \end{eqnarray}$$
答え
$$b=3\sqrt{6}$$
【正弦定理の問題】辺の大きさを求める②
△ABCにおいて、次のものを求めよ。
$$A=135°, R=4のとき、a$$
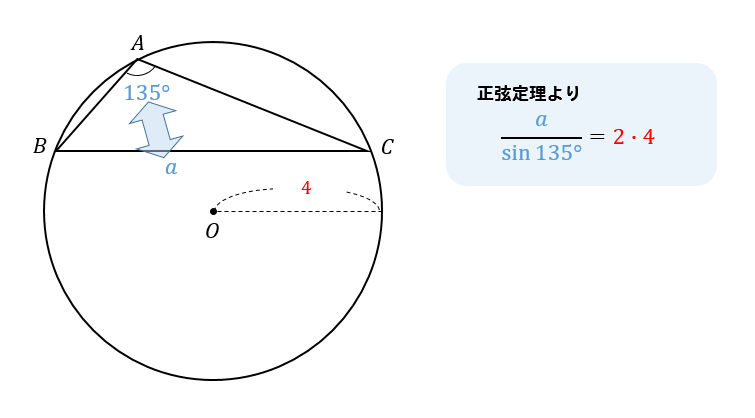
外接円の半径が分かっている場合には
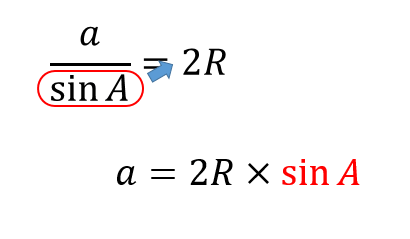
このように式を変形させるとよいです。
$$\begin{eqnarray}\frac{a}{\sin 135°}&=&2\cdot 4\\[5pt]a&=&8\times \sin 135°\\[5pt]a&=&8\times \frac{1}{\sqrt{2}}\\[5pt]a&=&\frac{8}{\sqrt{2}}\\[5pt]a&=&4\sqrt{2} \end{eqnarray}$$
答え
$$a=4\sqrt{2}$$
【正弦定理の問題】外接円の半径を求める
△ABCにおいて、次のものを求めよ。
$$A=135°, a=7のとき、R$$
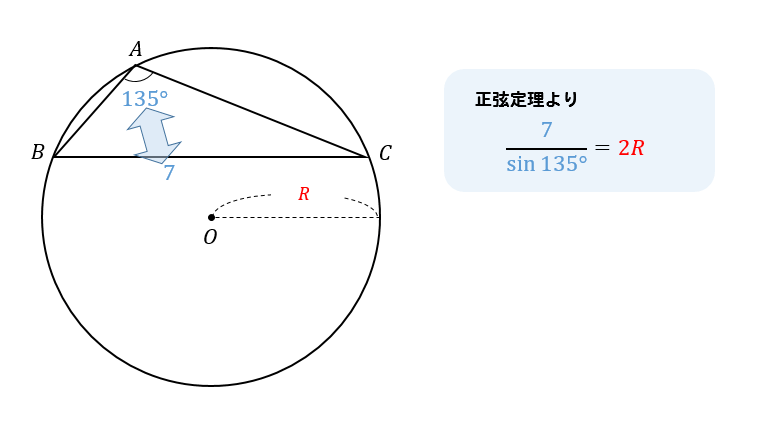
外接円の半径を求める場合
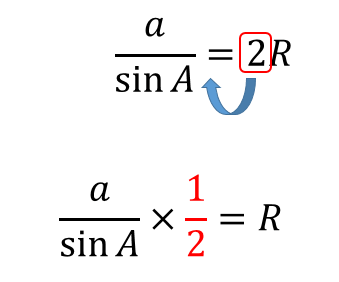
このように式変形して計算していくとよいです。
$$\begin{eqnarray}\frac{7}{\sin 135°} &=&2R\\[5pt]\frac{7}{\sin 135°}\times \frac{1}{2}&=&R\\[5pt]\frac{7}{\frac{1}{\sqrt{2}}}\times \frac{1}{2}&=&R\\[5pt]7\times \frac{\sqrt{2}}{1}\times \frac{1}{2}&=&R\\[5pt]R&=&\frac{7\sqrt{2}}{2}\end{eqnarray}$$
答え
$$R=\frac{7\sqrt{2}}{2}$$
【正弦定理の問題】角の大きさを求める
△ABCにおいて、次のものを求めよ。
$$a=3, b=\sqrt{6}, A=60°のとき、B$$
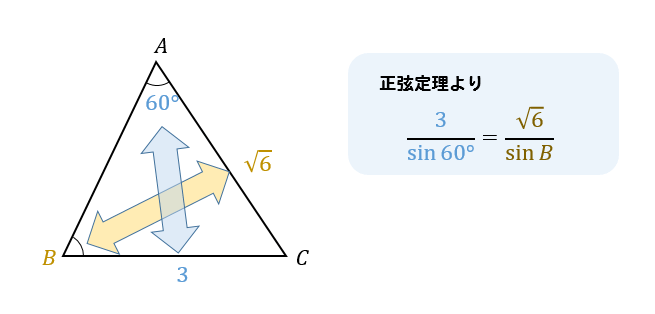
角の大きさを求めたい場合
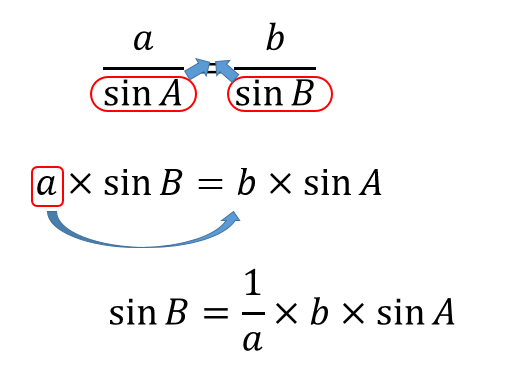
このように式変形して計算していくとよいです。
$$\begin{eqnarray}\frac{3}{\sin 60°}&=&\frac{\sqrt{6}}{\sin B}\\[5pt]3\sin B&=&\sqrt{6}\sin 60°\\[5pt]\sin B&=&\frac{1}{3}\times \sqrt{6}\times \frac{\sqrt{3}}{2}\\[5pt]\sin B&=&\frac{3\sqrt{2}}{6}=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\\[5pt]B&=&45° \end{eqnarray}$$
答え
$$B=45°$$
【追加演習】正弦定理の式変形、計算を極める!
ここまでのところでそれぞれの正弦定理の使い方は理解してもらえましたか??
正弦定理は分数やルートなど、式変形や計算がややこしくてミスが多くなりがちです…ここを完璧にして確実に点をゲットするためには、徹底的な計算練習が不可欠だ!!
というわけで、今回は追加の演習プリントを用意しました。これに取り組むことで、ややこしい分数、ルートの計算もスラスラと解けるようになりますので、ぜひ最後の仕上げとしてチャレンジしてみましょう。

この追加プリントはメルマガ講座用のサイトで公開しています!講座は無料で受講することができますので、下のフォームから今回の課題を受け取っておいてくださいね!
【追加演習】正弦定理の式変形、計算を極めるぞ!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用ください^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
正弦定理まとめ!
お疲れ様でした!
以上、正弦定理の使い方についてでした。
正弦定理の公式を覚えるためには、式とにらめっこするよりも手を動かして問題をたくさん解くのがおすすめです。
問題を解いているうちに、この辺の位置関係なら…正弦定理だ、余弦定理だ!
ということも理解できるようになるはずです(^^)
正弦定理について理解が深まったら、次は余弦定理!
しっかりとマスターしていきましょう(^^)
>【余弦定理の公式】覚え方はどうする?角度の求め方などを解説!
















コメントを残す