今回は高校数学Ⅰで学習する三角比の単元から
「どんな三角形になる?三角形の形状決定」
についてイチから解説していきます。
見た目が難しいなので、質問をいただくことが多い問題です。
ですが、これから紹介していくポイントをおさえておけば簡単に解けるようになりますよ^^
というわけで!
今回は次の3つの問題を活用しながら形状決定のコツを身につけていきましょう(‘ω’)ノ
【今回取り上げる3題】
△ABCにおいて、次の等式が成り立つとき、△ABCはどんな形の三角形か。
(1) \(\sin{A}=2\cos{B}\sin{C}\)
(2)\(a\sin{A}+b\sin{B}=c\sin{C}\)
(3)\(a\cos{A}=b\cos{B}\)
今回の内容をサクッと理解したい方はこちらの動画もご参考ください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
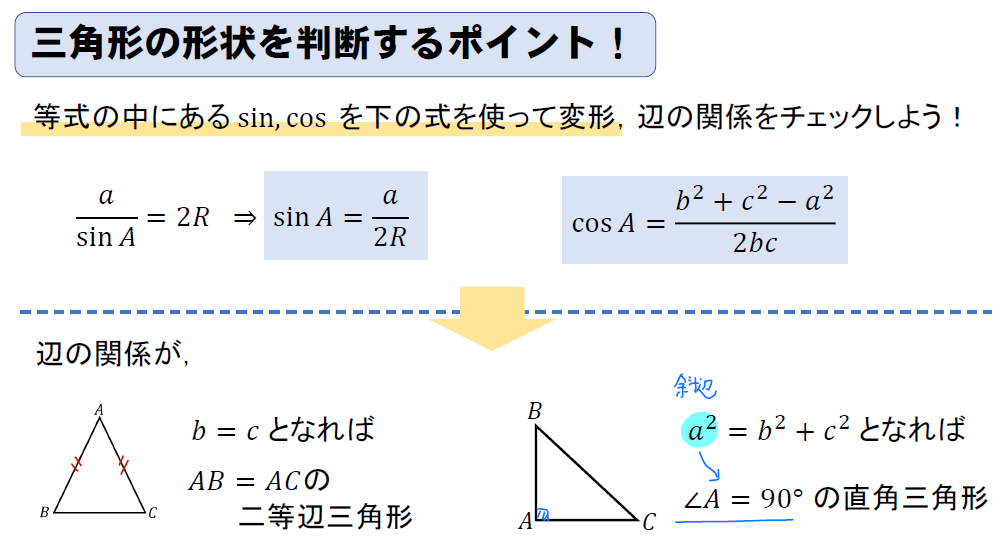
三角形の形状を判断するポイント!
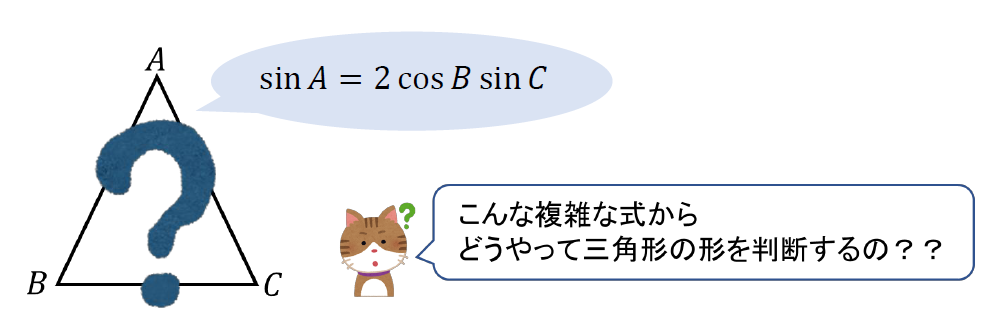
与えられた等式を眺めているだけでは、どんな三角形になるのか全く判断できません(^^;)
そこで!
まずは等式の中にある\(\sin , \cos \)を正弦定理、余弦定理を使って変形します。

すると、辺の関係式ができあがりますね。
できあがった辺の関係式を見ながら次のように判断します。
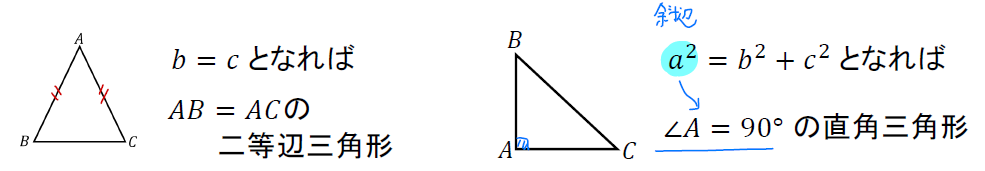
というわけで、三角形の形状を判断する流れとしては以下の通りです。
- \(\sin , \cos \)を変形して辺だけの式を作り、その関係をチェックする。
- ①の式が「\(b=c\)」のような形になれば二等辺三角形、「\(a^2=b^2+c^2\)」のような形になれば直角三角形と判断できる
それでは、実際に問題を見ながら解き方をチェックしていきましょう!
どんな三角形になる?【問題①】
△ABCにおいて、次の等式が成り立つとき、△ABCはどんな形の三角形か。
(1) \(\sin{A}=2\cos{B}\sin{C}\)
使った変形
$$\sin{A}=\frac{a}{2R}$$
$$\sin{C}=\frac{c}{2R}$$
$$\cos{b}=\frac{a^2+c^2-b^2}{2ac}$$
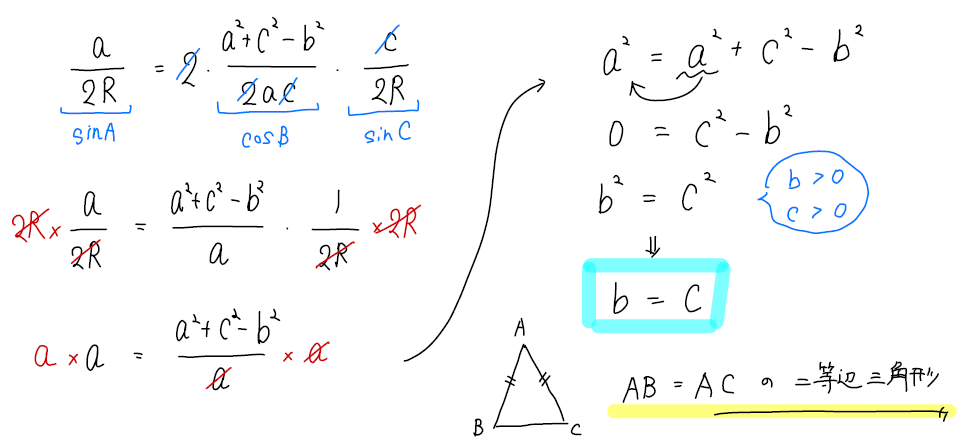
まずは上の式を使って\(\sin, \cos \)を変形する。
そして、分母にある\(2R, a\)を払って消す。
そこから地道に式を整理してまとめていくと「\(b=c\)」という関係式を導くことができます。
これで二等辺三角形であることが確かめられましたね^^
慣れるまでは途中式の変形が大変かもしれませんが、やっていくことは地道な計算だけですね!
どんな三角形になる?【問題②】
使った変形
$$\sin{A}=\frac{a}{2R}$$
$$\sin{B}=\frac{b}{2R}$$
$$\sin{C}=\frac{c}{2R}$$
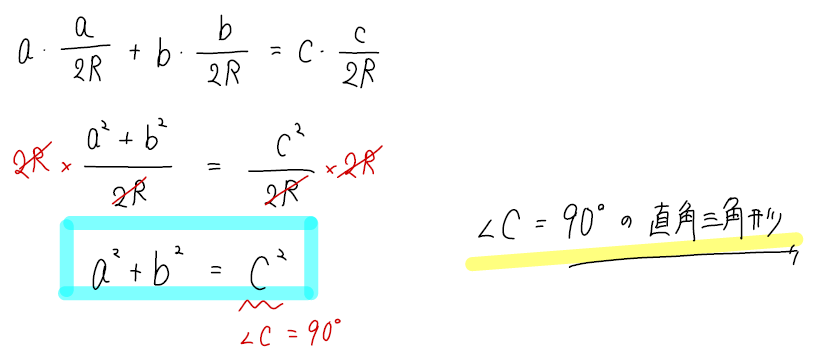
まずは上の式を使って\(\sin, \cos \)を変形する。
そして、分母にある\(2R\)を払って消す。
すると「\(a^2+b^2=c^2\)」という関係式を導くことができます。
このように2乗の関係式になれば直角三角形であることが判断できますね!
どんな三角形になる?【問題③】

使った変形
$$\cos{a}=\frac{b^2+c^2-a^2}{2bc}$$
$$\cos{b}=\frac{a^2+c^2-b^2}{2ac}$$
初めに\(\cos \)を変形するという流れはこれまで通りなのですが、それ以降の式変形が複雑です(^^;)
「分母を払う ⇒ 次数の低い文字で整理する ⇒ 共通因数でくくり出す」
この流れで変形していけば、なんとか式をコンパクトにまとめていくことができます。
この辺はテキストだけでは伝わりにくいです。こちらの動画で途中式をていねいに解説しているので参考にしてくださいね^^
まとめ
三角形の形状を判断するためには以下の流れで式変形をしていきましょう。
そして、等式を変形するためには正弦定理、余弦定理を使った以下の変形をしっかりと覚えておくことが大事です!
$$\sin{B}=\frac{b}{2R}$$
$$\sin{C}=\frac{c}{2R}$$
$$\cos{a}=\frac{b^2+c^2-a^2}{2bc}$$
$$\cos{b}=\frac{a^2+c^2-b^2}{2ac}$$
$$\cos{c}=\frac{a^2+b^2-c^2}{2ab}$$
途中の式変形については、たくさんの問題に触れながら慣れていくようにしましょうね^^

















初歩的な質問で申し訳ないのですが、問題2の
分母の2R+2Rが4Rにならないのはなぜですか?
分母同士は足されないからですよ^^