\(\sin75°,\cos75°,\tan75°\)の求め方についてサクッと解説します。
やり方としては、
- 数学Ⅱで学習する加法定理を用いたもの
- 数学Ⅰで学習する三角比の図形を用いたもの
があります。
それぞれのやり方について確認していきましょう。
【数学Ⅱ】加法定理を用いた求め方
【加法定理】
$$\sin(α\pmβ)=\sinα\cosβ\pm \cosα\sinβ$$
$$\cos(α\pmβ)=\cosα\cosβ\mp \sinα\sinβ$$
$$\tan(α\pmβ)=\frac{\tanα\pm\tanβ}{1\mp \tanα\tanβ}$$
数学Ⅱで学習する加法定理を用いると75°の三角比は簡単に求めることができます(^^)
$$75°=30°+45°$$
このように、75°は30°と45°の有名角に分けることができます。
これを用いて加法定理で計算すると…



このように加法定理を用いることで計算ができますね!
ただし、\(\tan75°\)に関してはすでに\(\sin75°,\cos75°\)を求めている場合
次のように相互関係を用いて計算するとラクになります。
三角比の相互関係
$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$

$$\sin75°=\frac{\sqrt{2}+\sqrt{6}}{4}$$
$$\cos75°=\frac{\sqrt{6}-\sqrt{2}}{4}$$
$$\tan75°=2+\sqrt{3}$$
ちなみに、\((90-\theta)\)の関係を用いると75°から15°への変換も可能になります。
\((90-\theta)\)の関係
$$\sin(90-\theta)=\cos\theta$$
$$\cos(90-\theta)=\sin\theta$$
$$\tan(90-\theta)=\frac{1}{\tan\theta}$$
$$\begin{eqnarray}\sin15°&=&\sin(90°-75°)\\[5pt]&=&\cos75°\\[5pt]&=&\frac{\sqrt{6}-\sqrt{2}}{4} \end{eqnarray}$$
$$\begin{eqnarray}\cos15°&=&\cos(90°-75°)\\[5pt]&=&\sin75°\\[5pt]&=&\frac{\sqrt{2}+\sqrt{6}}{4} \end{eqnarray}$$
$$\begin{eqnarray}\tan15°&=&\tan(90°-75°)\\[5pt]&=&\frac{1}{\tan75°}\\[5pt]&=&\frac{1}{2+\sqrt{3}}\\[5pt]&=&2-\sqrt{3} \end{eqnarray}$$
【数学Ⅰ】図形を使って求める方法
基本的には上で紹介したように加法定理を用いて求めればよいです。
しかし、加法定理を学習していない高校1年生の範囲では、次のように図を用いて75°の三角比を求めさせる問題が出題されます。
【問題】
次の図を用いて、\(\sin75°,\cos75°\tan75°\)を求めよ。

まずは、60°、30°、90°になっている直角三角形から\(1:2:\sqrt{3]\)の比を用いて辺を出します。
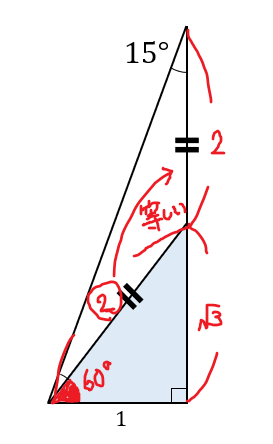
そこから三平方の定理を用いて全体の三角形の辺の長さを求めましょう。
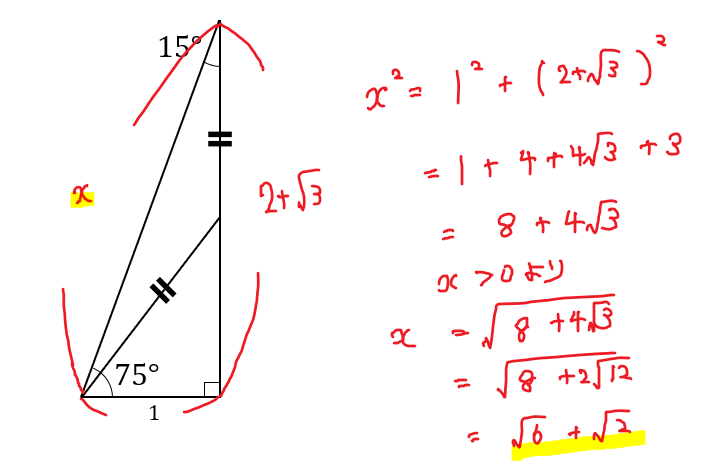
二重根号の計算をしているので、ちょっとややこしいですが(^^;)
参考:ルートの中にルート!?二重根号のはずし方について解説!
これにて、三角形の辺がすべて揃ったことになります。
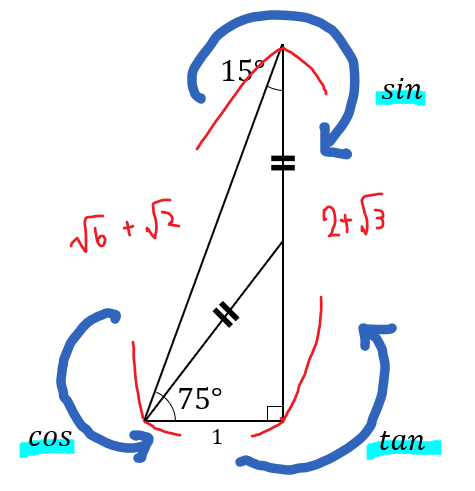
あとはこれらの辺を用いて三角比の値を求めればOKですね。
$$\begin{eqnarray}\sin75°&=&\frac{2+\sqrt{3}}{\sqrt{6}+\sqrt{2}}\\[5pt]&=&\frac{(2+\sqrt{3})(\sqrt{6}-\sqrt{2})}{4}\\[5pt]&=&\frac{\sqrt{6}+\sqrt{2}}{4} \end{eqnarray}$$
$$\begin{eqnarray}\cos75°&=&\frac{1}{\sqrt{6}+\sqrt{2}}\\[5pt]&=&\frac{\sqrt{6}-\sqrt{2}}{4} \end{eqnarray}$$
$$\begin{eqnarray}\tan75°&=&\frac{2+\sqrt{3}}{1}\\[5pt]&=&2+\sqrt{3} \end{eqnarray}$$
まとめ!
75°の三角比の値を求めたい場合、基本的には加法定理を覚えていればOKです。
加法定理を用いると15°、75°、105°など
中途半端な角度であっても有名角を使って分解して求めることができますね!
高校1年生で加法定理を学習していない場合、三平方の定理、直角三角形の比などを用いて辺の長さを求めましょう。
すると、それぞれの辺を見比べることで三角比の値を求めることができますね(/・ω・)/


















コメントを残す