今回は分母と分子に分数が含まれているときの計算方法について解説していきます。
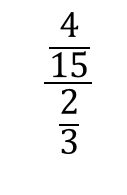
あれ…
上と下、両方に分数があるぞ。
どうやって計算するんだ!?

こんな感じで
この問題は非常に質問が多いです。
見慣れない形であることに加えて
見た目がすっごく難しそうに見えちゃうからね。
でも、基本をおさえておけば
何てことない計算方法なので
今回の記事を通して
しっかりとやり方を覚えていきましょう!
分母と分子に分数があるときの計算のやり方とは
結論から言ってしまうと
この分数の計算はこのようにやっていきます。
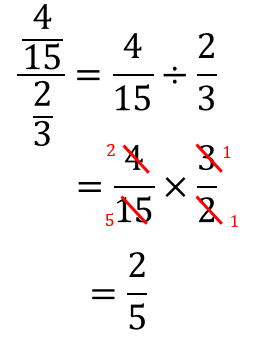
分子の数と分母の数を割り算して計算していますね。
なぜ、このような計算の仕方をするのかを
2つの視点から解説していきます。
分数は(分子)÷(分母)で表せる。
分数の基本的な考え方を思い出して欲しいのですが
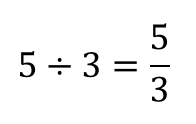
割り算はこのように分数の形で表すことができましたよね。
これを逆に考えれば
分数も当然、割り算の形で表せるということになります。

このように
分数は上(分子)÷下(分母)で表すことができます。
この考え方から
分母と分子が分数になったとしても
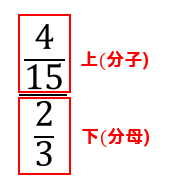
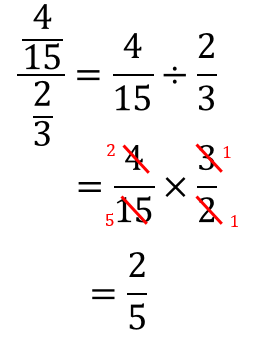
このように計算できるというわけです。
この計算に慣れてきた人は、このように割り算部分を省略して
分母をひっくり返して、分子にかける
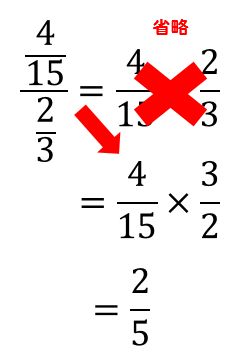
と覚えておいても良いです。
分母を1にする数を分母、分子にかける
次は、分母を1にする数が掛けるという発想です。
分数は、分母と分子に同じ数をかけても
値は変わらないという特徴があります。
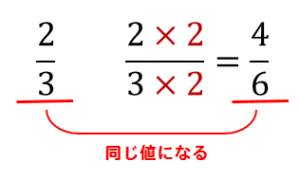
この考え方を利用して
分数分の分数という複雑な形を解消するために
分母の逆数を、分母分子の両方に掛けてやります。
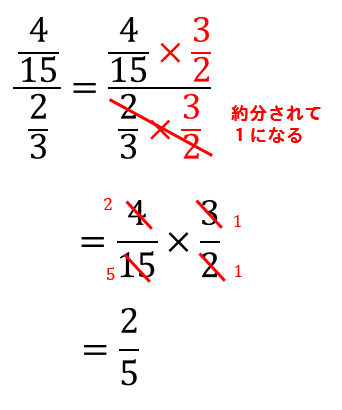
そうするとこのように計算ができます。
結局は、分母をひっくり返して分子にかけるという
さっきと全く同じ式になるのですが
この式の導き方がいろいろあるんだなってことで
頭に入れておいてもらえればと思います。
演習問題で理解を深める!
それでは、計算方法がわかったところで
いろんな分数を計算していきましょう。
問題
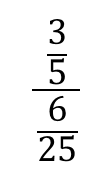
問題
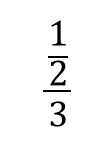
問題
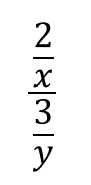
最後は、高校生レベル!
問題
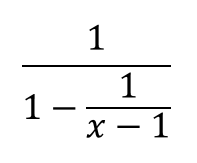
分数分の分数のやり方 まとめ
分数の中に分数!
こんな形が出てきたときには
上÷下
つまり、分子÷分母の計算を解いていけば
答えを出すことができます!
見た目は難しそうに見えますが
単純な割り算を計算するだけですからね
しっかりと練習して身につけていきましょう!


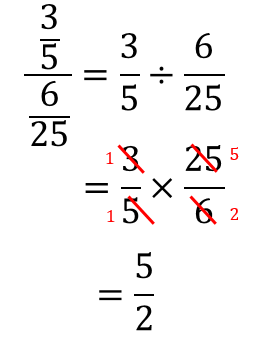
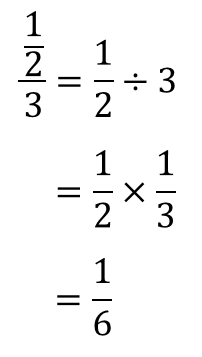
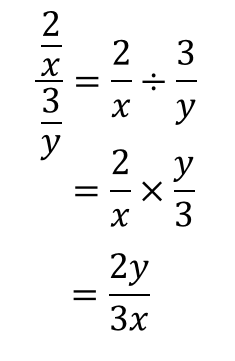
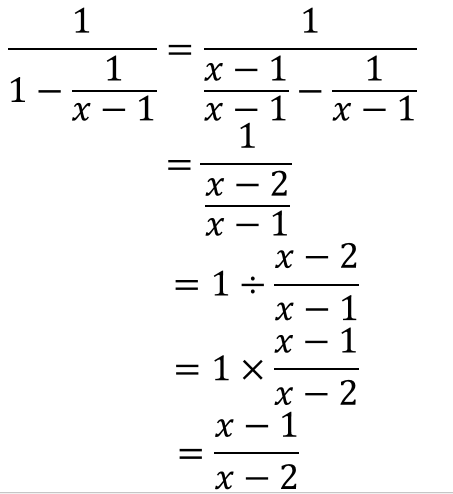








はじめまして。
「分数に分数」で検索してたどり着きました。
むちゃくちゃ分かりやすかったです!ありがとうございます!!
こちらこそありがとう
コメントありがとうございます!
すこしでもお役に立てたのであれば嬉しい限りです(^^)
このタイプの問題が本当に解けなくて困っていたので助かりました!
ありがとうございます!!
お役に立ててうれしいです^^
すげぇわかりやすい…
ありがとうございます!!
つまりが解消されました。マジでありがとうございました。
お役に立ててよかったです^^
高2ですが役に立ちました
小5です
すごく役に立ちました
ありがとう!
役立った
わかりました