今回は高校数学Ⅰで学習する三角比の単元から「三角比の拡張」についてイチから解説していきます。
こちらで学習していただいたように、90°までの鋭角であれば直角三角形の辺を見比べながら三角比の値を求めることができました。
では、90°より大きい鈍角や0°、90°、180°といった角の場合にはどのように考えればよいのでしょうか。
それぞれの求め方、考え方について確認していきましょう(‘◇’)ゞ
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
三角比の拡張
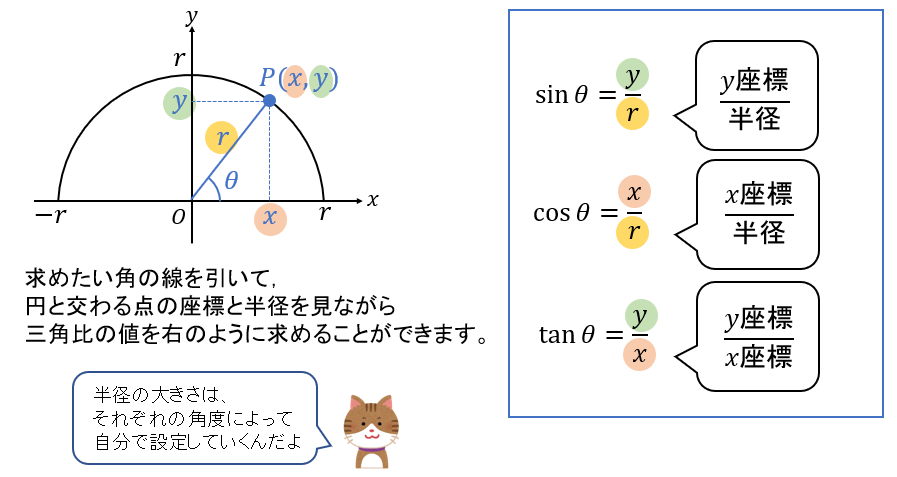
90°を超える鈍角を考える場合には、上のように半円と座標を用いて三角比の値を考えます。
とはいえ、上の図だけではちょっとイメージが掴みづらいと思うので次の章で具体的な求め方と手順を見ていきましょう。
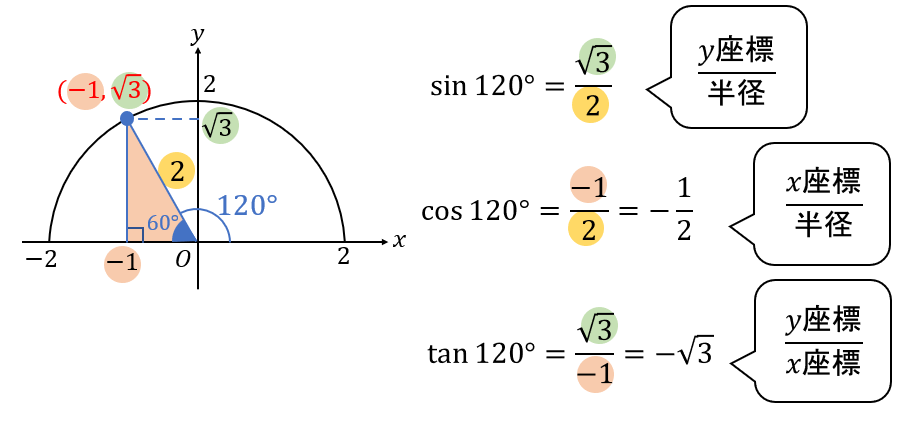
120°のとき
まずは半円をかいて、120°になる線をかき入れましょう。
円の半径については後から考えていくようになるので、今の段階ではスルーしておきます。
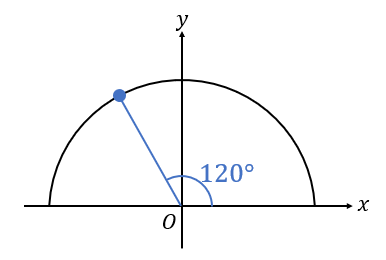
円との交点に点をとり、そこから\(x\)軸に対して真っすぐな線を引き、直角三角形を作ります。
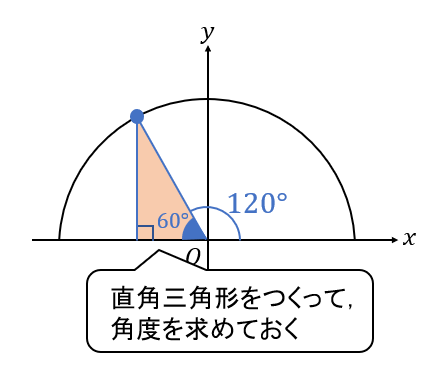
次に、この直角三角形に注目して、辺の比を考えていきましょう。
今回は60°の直角三角形だから「\(1:2:\sqrt{3}\)」であることがわかりますね。
ここでポイント!
円の半径についてスルーしていましたが、ここで出てきた
「斜辺の比である\(2\)」を半径として設定します。
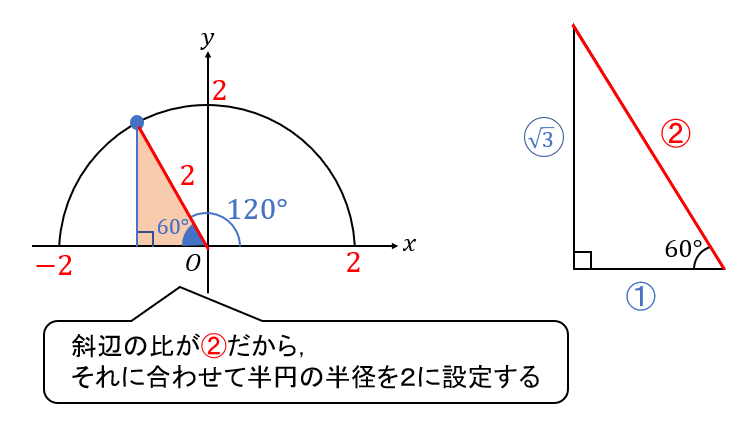
半径を設定したことで、交点の座標がこのように求まります。
座標が求まったら、半径と座標を見比べながら三角比の値を求めます。
では、手順をまとめておきますね。
- 半円をかいて、角度の線を書き入れる。このとき、半径の大きさはスルーします。
- 円との交点から真っすぐ下に線を引き、直角三角形を作ります。この三角形の比を考え、斜辺にあたる比の大きさを半径に設定します。
- 半径が決まることで交点の座標が分かるので、そこから三角比の値を求める。
ちょっと慣れるまでは大変かもしれませんね(^^;)
では、135°と150°についても同じように考えてやってみましょう。
【答】
$$\sin{120°}=\frac{\sqrt{3}}{2}$$
$$\cos{120°}=-\frac{1}{2}$$
$$\tan{120°}=-\sqrt{3}$$
135°のとき
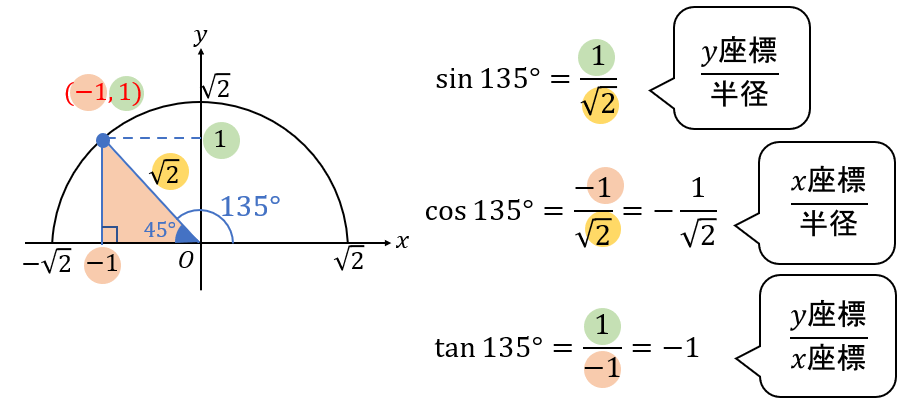
ここでは45°の直角三角形ができるので、\(\sqrt{2}\)を半径に設定して座標を求めていきましょう。
【答】
$$\sin{135°}=\frac{1}{\sqrt{2}}$$
$$\cos{135°}=-\frac{1}{\sqrt{2}}$$
$$\tan{135°}=-1$$
150°のとき
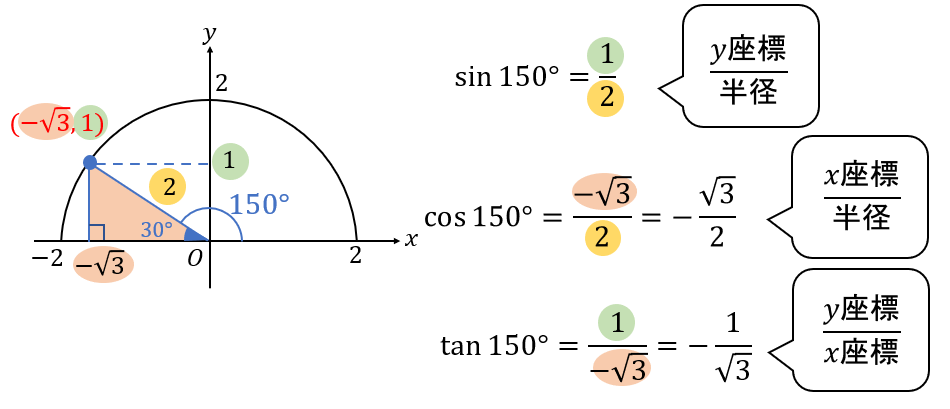
ここでは30°の直角三角形ができるので、\(2\)を半径に設定して座標を求めていきましょう。
【答】
$$\sin{150°}=\frac{1}{2}$$
$$\cos{150°}=-\frac{\sqrt{3}}{2}$$
$$\tan{150°}=-\frac{1}{\sqrt{3}}$$
単位円を使って三角比の値を求める
これまではそれぞれの角度によって半円の半径を設定して考えましたが、最初から半径を1に設定して考えると次のようになります。
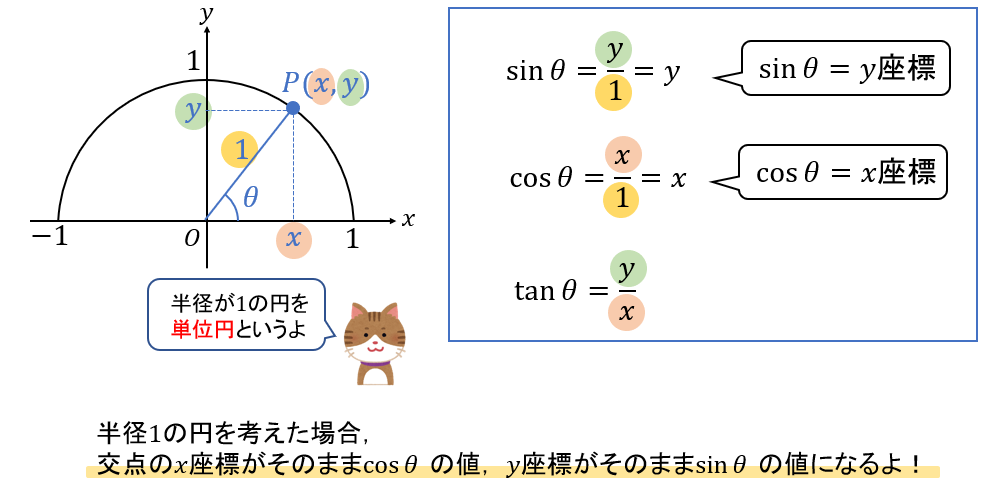
この場合では、交点の座標を読み取って、その\(x\)座標をそのまま\(\cos{\theta}\)の値、\(y\)座標をそのまま\(\sin{\theta}\)の値と考えることができます。
この考え方は、次に取り上げる「0°,90°,180°」のような角のときに活用されます。
0°のとき
単位円(半径1)をかいて、0°の座標を求めます。
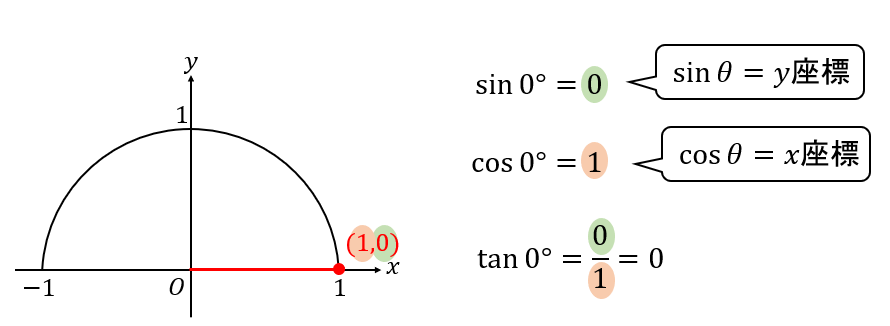
その座標からそれぞれの値が簡単に求まりますね!
【答】
$$\sin{0°}=0$$
$$\cos{0°}=1$$
$$\tan{0°}=0$$
90°のとき
単位円(半径1)をかいて、90°の座標を求めます。
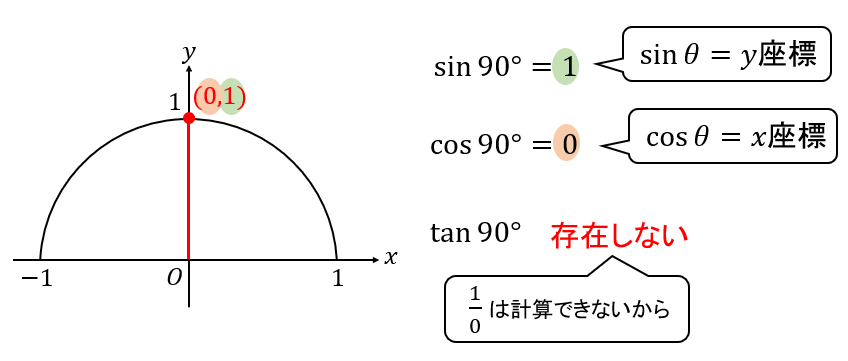
注意しておきたいのが、
\(\tan{90°}\)は存在しない!ということです。
計算しようとすると分母に0がきてしまい、計算できなくなります。
そのため、\(\tan{90°}\)は定義されません。
【答】
$$\sin{90°}=1$$
$$\cos{90°}=0$$
$$\tan{90°} 存在しない$$
180°のとき
単位円(半径1)をかいて、180°の座標を求めます。
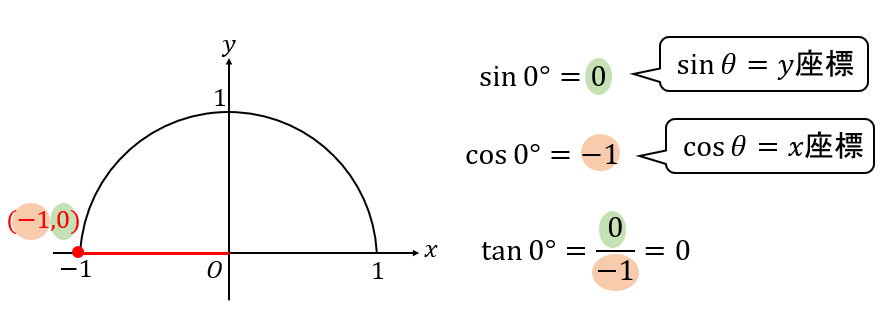
【答】
$$\sin{180°}=0$$
$$\cos{180°}=-1$$
$$\tan{180°}=0$$
【追加演習】三角比の値を徹底特訓だ!!
ここまでのところでそれぞれの三角比の値の求め方は理解してもらえましたか??
ここからは理解を定着させるための演習課題を用意しました。ここはとにかく量をこなして、反射的に値が答えられるようになるまで特訓してもらいたいです!というわけで、このプリントを活用して徹底的に基礎を叩き込んでください!

この追加プリントはメルマガ講座用のサイトで公開しています!講座は無料で受講することができますので、下のフォームから今回の課題を受け取っておいてくださいね!
【追加演習】三角比の値を徹底的に特訓するぞ!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用ください^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ!
お疲れ様でした!
半円を使った三角比の求め方はバッチリですか??
「半径をあとから設定して考えるパターン」
「初めから半径を1に設定して考えるパターン」
この2パターンの考え方がありましたが、
120°、135°、150°のように直角三角形がつくれる場合には、半径をあとから設定。
0°、90°、180°のように直角三角形がつくれない場合には、半径を1に設定。
このように使い分けていくと便利ですね!
これらの考え方が慣れてくると、解説動画の中で紹介していたようなやり方をしていくと素早く求めれるようになりますよ^^
解説動画はこちら!

















三角比の拡張では、180度を超えるyがマイナスとなる世界を扱わないのはなぜでしょうか?
三角比の単元では0°~180°を扱います。
180°を超える場合については数学Ⅱの三角関数で扱うようになります!
中高一貫のカリキュラムではちょっと違うかもしれませんが(^^;