高校数学Ⅰで学習する三角比の単元から
「二等辺三角形を用いて36°の三角比を求める」
について解説していきます。
【問題】(ニューアクションβより)
\(AB=AC\),\(∠A=36°\) の二等辺三角形\(ABC\) について,\(∠C\) の二等辺三角形が辺 \(AB\) と交わる点を \(D\) とする。
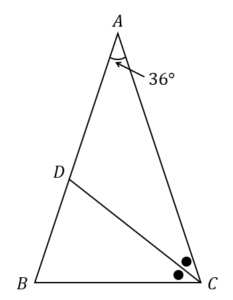
(1)\(BC=1\) とするとき,\(BD\),\(AC\) の長さを求めよ。
(2)\(\cos 36°\) の値を求めよ。
(3)\(\sin18°\) の値を求めよ。
これはニューアクションβに掲載されており、
解き方が分かりにくい…!
ということで、よく質問をいただく問題です。
イチからでも理解できるよう解説をつけていくので、ぜひ参考にしてみてくださいね!
今回の記事はこちらの動画でも解説しています(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(1)の解説!相似な図形に注目!
△ABCは二等辺三角形なので、底角である \(∠B\) と \(∠C\) の大きさが等しくなります。
よって、それぞれの角の大きさは次のようになります。
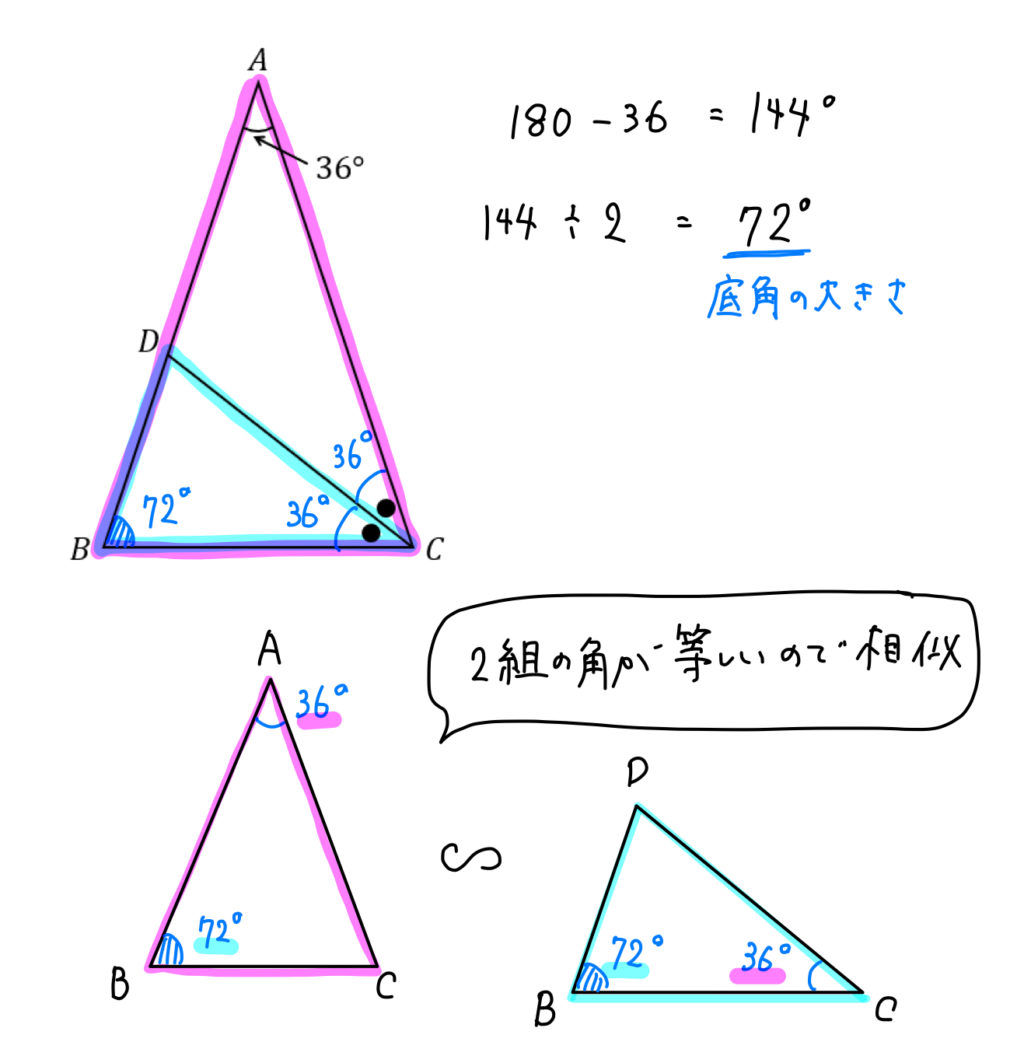
すると、2つの角がそれぞれ等しいことから、
このように相似な三角形を見つけることができます。
相似な図形を見つけたことから、相似比を使いながら \(BD, AC\) の長さを求めていきます。
相似比を用いるにあたって、\(BD=x\) とし、他にも長さが表せるところを書き込んでおくと次のようになります。
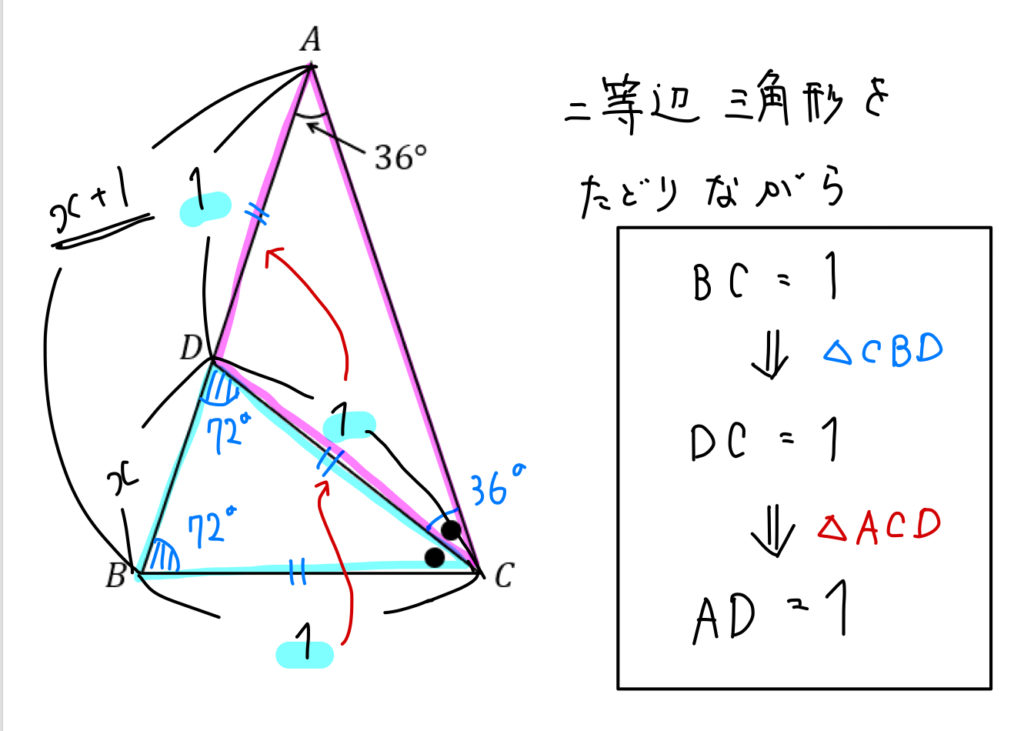
二等辺三角形を見つけることができるので、それをたどっていくと、\(AB=x+1\) と表せますね。
これを用いて相似比をとっていくと、次のように \(x\) を求めることができます。
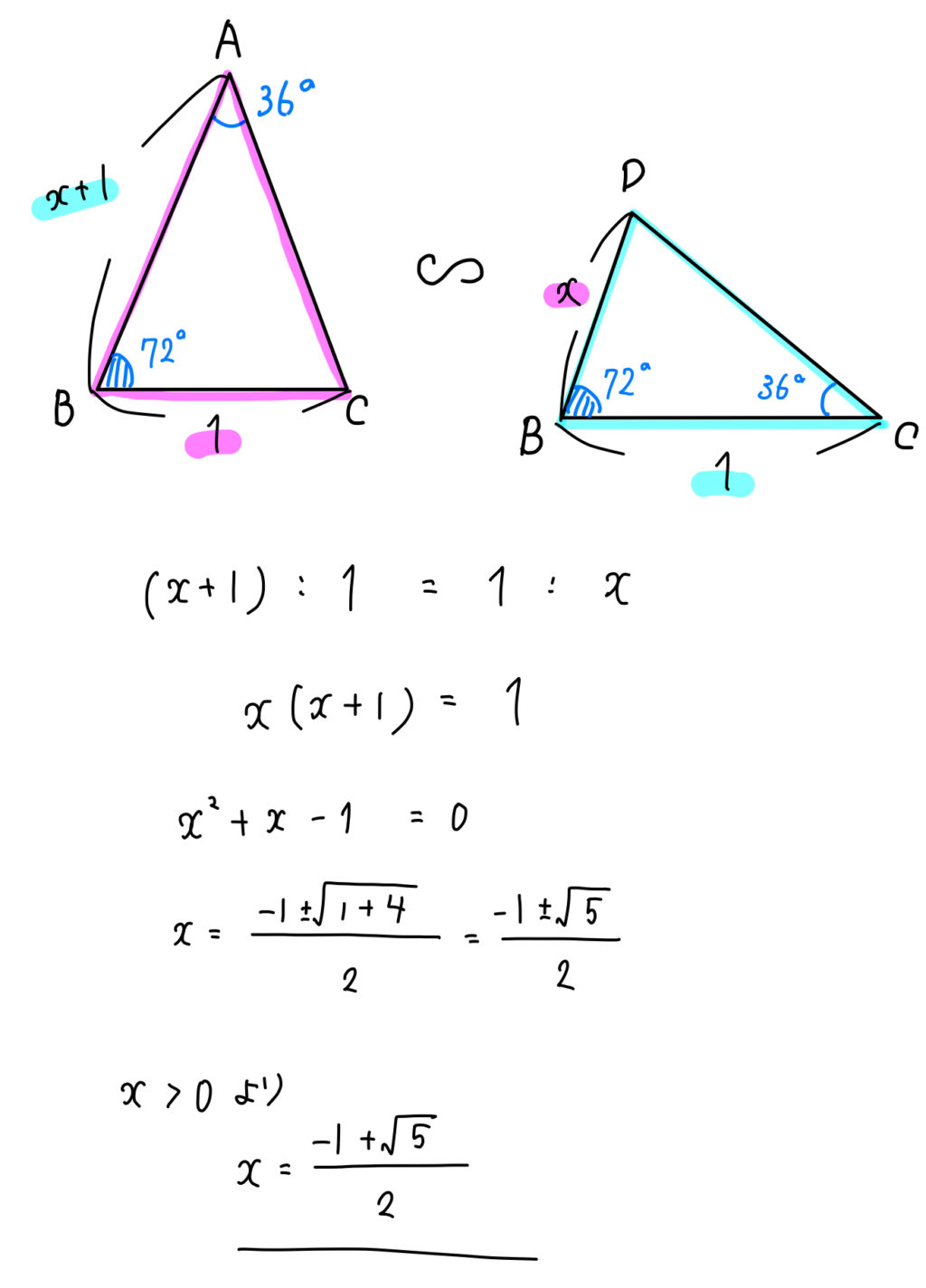
\(x=\frac{-1-\sqrt{5}}{2}\) は負になってしまうので、長さを表す値としては不適ですね。
よって、\(BD=\frac{-1+\sqrt{5}}{2}\) となります。
さらに、\(AC=AB\) より
\(AC=1+\frac{-1+\sqrt{5}}{2}=\frac{1+\sqrt{5}}{2}\) となります。
答え
\(BD=\frac{-1+\sqrt{5}}{2}\)
\(AC=\frac{1+\sqrt{5}}{2}\)
(2)の解説!直角三角形を作る!
36°の三角比の値を求めるためには、36°の角を含む直角三角形を作ってやることがポイントです。
(1)で求めた辺の大きさを利用できる直角三角形を次のように作ってやります。
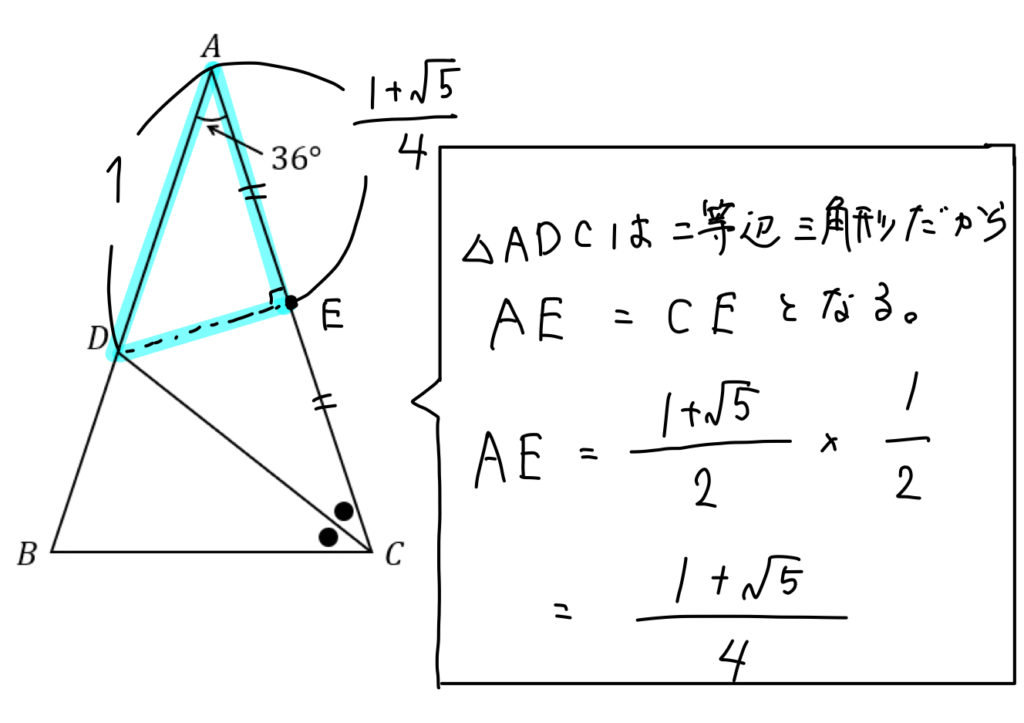
そして、この直角三角形の斜辺と底辺に当たる部分を見ていけば \(\cos\) の値が求まりますね!
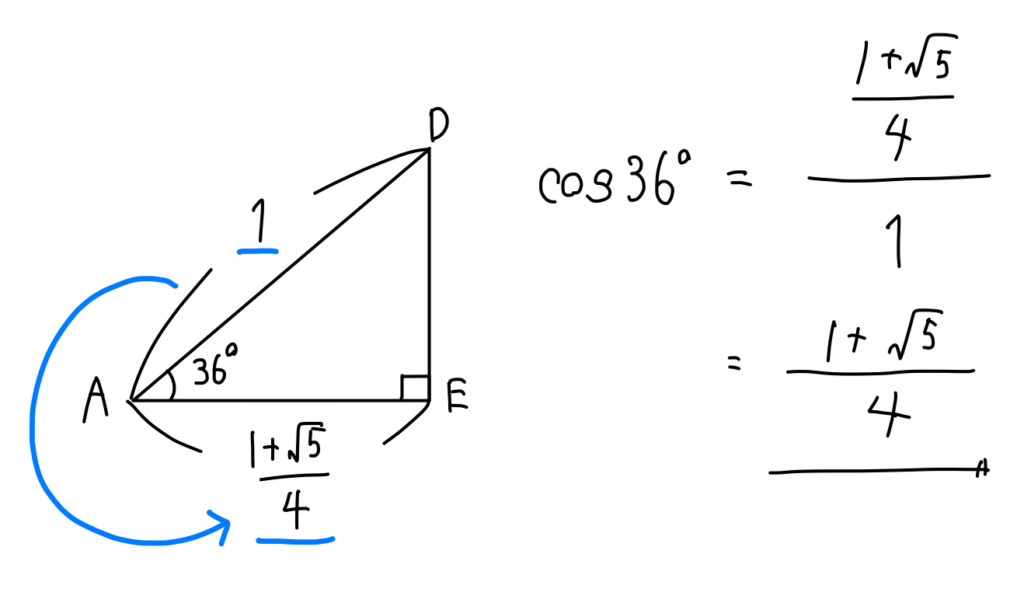
答え
$$\cos36°=\frac{1+\sqrt{5}}{4}$$
(3)の解説!18°を含む直角三角形はどこ?
こちらも(2)と同じように、18°の角を含む直角三角形を作るのがポイントです。
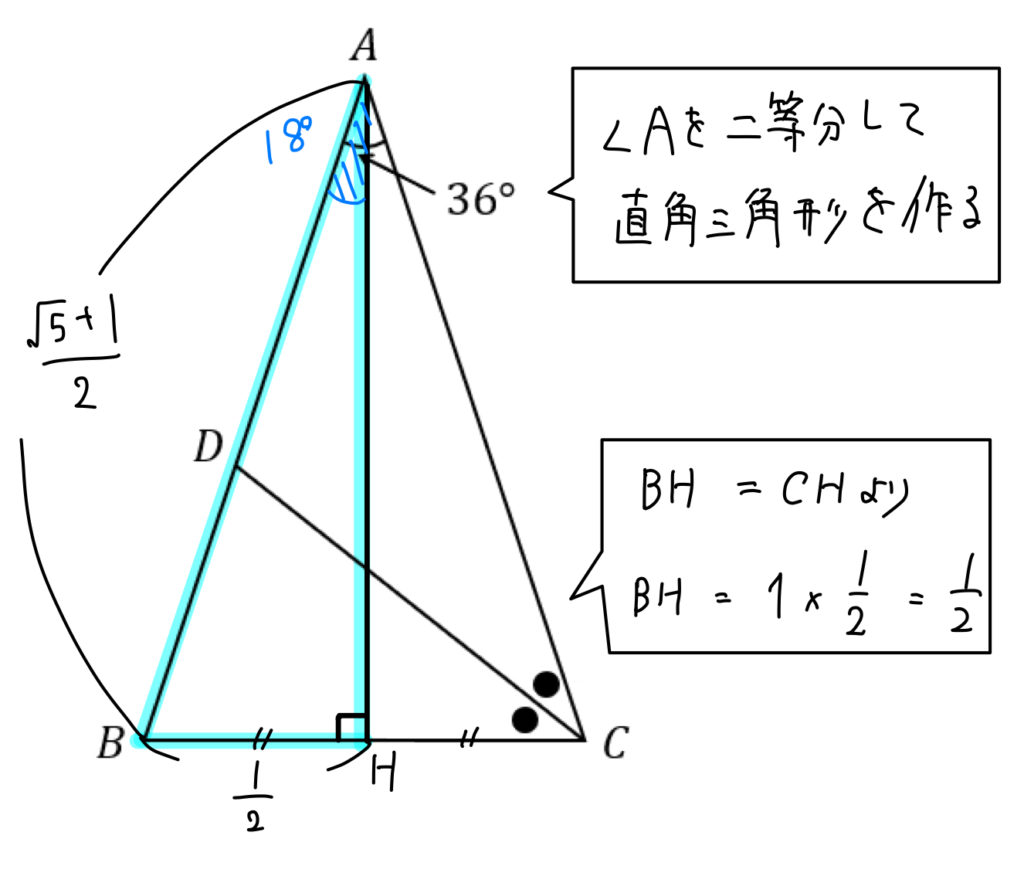
この直角三角形に注目すれば、これまで求めてきた長さを用いて簡単に求めることができますね。
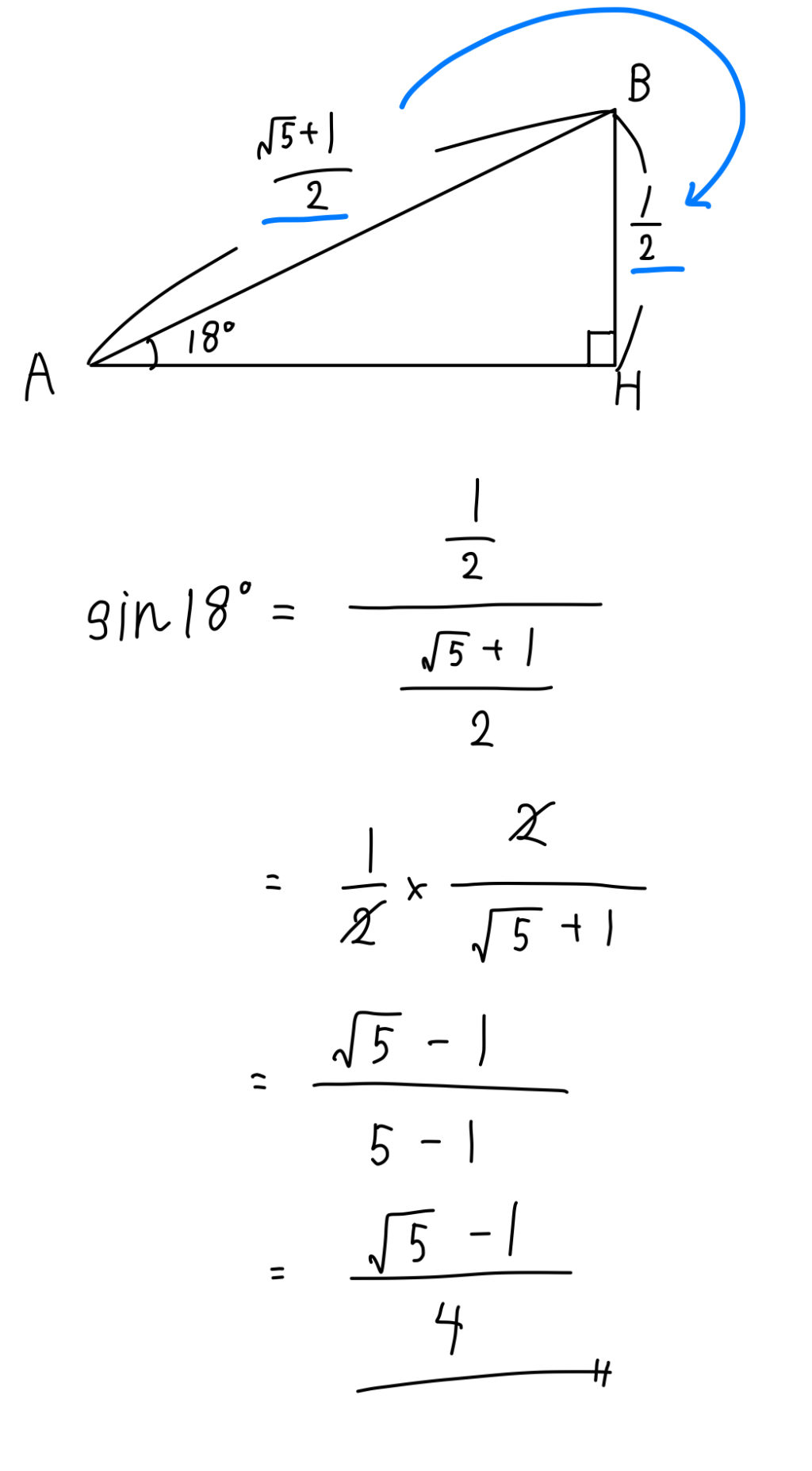
答え
$$\sin18°=\frac{\sqrt{5}-1}{4}$$
まとめ!
お疲れ様でした!
今回の問題は、補助線を引いたりする場面もあるので、
初見で解くのはちょっと難しいです(^^;)
ポイントとしては、相似比を利用して辺の長さを求めること。
そして、補助線を引いて直角三角形を作ること。
この2点をしっかりとおさえておいてくださいね!
















コメントを残す