今回は数学Ⅰで学習する三角比の単元から
「内接円の半径の求め方」
について解説していきます。
内接円とは、三角形の3辺すべてに接している円のことをいいます。
そして、三角形の面積と内接円の半径には次のような関係があります。
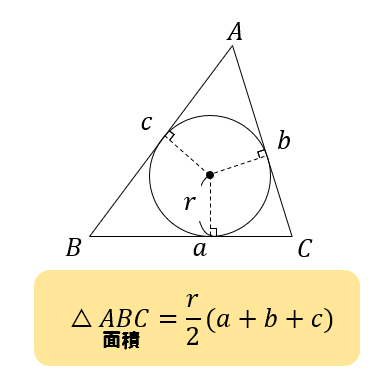
これを用いて、内接円の半径を求めるようになるので絶対に覚えておきたい公式です。
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
内接円の半径を求める手順
【問題】
\(△ABC\)において、\(a=4,b=3,c=2\)のとき、この三角形の内接円の半径の大きさを求めよ。
\(S=\frac{r}{2}(a+b+c)\)を使って\(r\)の値を求めればOKです。
まずは、三角形の面積を求めましょう。
面積の公式\(S=\frac{1}{2}bc\sin A\)を用いるため、\(\sin A\)の値を求めます。
角Aに注目して、余弦定理を用いると
$$\begin{eqnarray}\cos A&=&\frac{3^2+2^2-4^2}{2\cdot 3\cdot 2}\\[5pt]&=&\frac{-3}{12}\\[5pt]&=&-\frac{1}{4} \end{eqnarray}$$
ここから三角比の相互関係\(\sin^2 A +\cos^2 A=1\)を使って、\(\sin A\)に変換すると
$$\begin{eqnarray}\sin^2 A+\left(-\frac{1}{4}\right)^2&=&1\\[5pt]\sin^2 A&=&1-\frac{1}{16}\\[5pt]\sin^2 A &=&\frac{15}{16} \\[5pt]\sin A>0&\color{white}{=}&だから\\[5pt]\sin A&=& \frac{\sqrt{15}}{4}\end{eqnarray}$$
これでようやく\(\sin A\)の値が求まったので、面積の公式\(S=\frac{1}{2}bc\sin A\)に当てはめていきましょう。
$$\begin{eqnarray}S&=&\frac{1}{2}bc\sin A\\[5pt]&=&\frac{1}{2}\cdot 3\cdot 2\cdot \frac{\sqrt{15}}{4}\\[5pt]&=&\frac{3\sqrt{15}}{4}\end{eqnarray}$$
三角形の面積が求まったら
三角形の面積と内接円の半径の公式にあてはめる。
$$\begin{eqnarray}S&=&\frac{r}{2}(a+b+c)\\[5pt]\frac{3\sqrt{15}}{4}&=&\frac{r}{2}(4+3+2)\\[5pt]\frac{3\sqrt{15}}{4}&=&\frac{9}{2}r\\[5pt]r&=&\frac{3\sqrt{15}}{4}\cdot\frac{2}{9}\\[5pt]r&=&\frac{\sqrt{15}}{6}\cdots(解) \end{eqnarray}$$
- 三角形の面積を求める
- \(S=\frac{r}{2}(a+b+c)\)に当てはめて、方程式を解く。
- \(r\)の値が求まれば完成!
内接円の半径と三角形の面積のなぜ
\(S=\frac{r}{2}(a+b+c)\)の公式を使えばいいって分かったけど…
公式が覚えれない!
という方は、公式が成り立つ理由を知っておくといいです(^^)
円が内接している三角形は、内接円の中心と線を結ぶことで次のように3つに分割することができます。
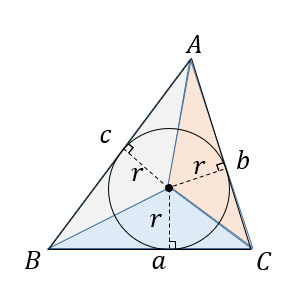
それぞれの三角形は底辺が\(a,b,c\)となり、高さは内接円の半径\(r\)と等しくなっています。
なので、それぞれの三角形の面積は\((底辺)\times (高さ)\times \frac{1}{2}\)で求めることができます。
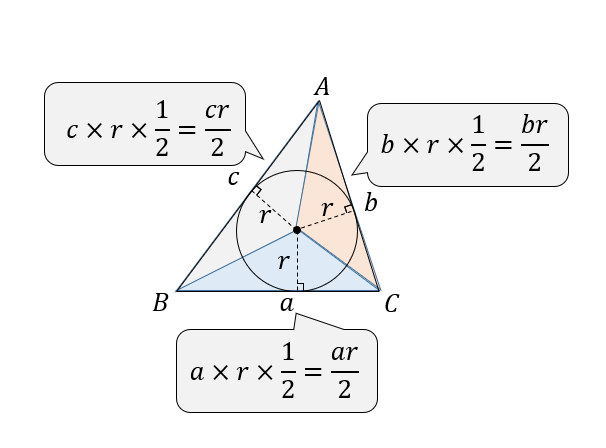
これらをすべて合わせると△ABCの面積となります。
よって、次のような式ができあがります。
$$\begin{eqnarray}S&=&\frac{ar}{2}+\frac{br}{2}+\frac{cr}{2}\\[5pt]&=&\frac{r}{2}(a+b+c) \end{eqnarray}$$
このように、三角形を分割して足し合わせることで公式が導けるということを知っていたら、公式を忘れてしまった時でも自分で思い出すことができるようになりますね!
内接円の半径を求める公式
\(S=\frac{r}{2}(a+b+c)\)の公式を変形することで、次のような公式を作ることができます。
$$\begin{eqnarray}S&=&\frac{r}{2}(a+b+c)\\[5pt]2S&=&r(a+b+c)\\[5pt]r&=&\frac{2S}{a+b+c} \end{eqnarray}$$
内接円の半径を求める公式
$$r=\frac{2S}{a+b+c}$$
内接円の半径に関する知識として、一応紹介しましたが…
まぁ、この公式を暗記して覚えている人は少ないと思います(^^;)
\(S=\frac{r}{2}(a+b+c)\)を変形しただけですからね。
どうしても時短したい!
式を短くしてスマートな解答を作りたい!
という方は、上記の公式を利用してみてください。
基本的には、\(S=\frac{r}{2}(a+b+c)\)の形にあてはめていけばOKです。
ヘロンの公式を使うとすこしラクになる
さて、ここまで内接円の半径を求めることについて解説をしてきましたが、手順の中で一番めんどうなのが三角形の面積を求めることですね。
ただ、このめんどうな手順もヘロンの公式を使うとラクに計算することができるようになります。
ヘロンの公式
\(\displaystyle{s=\frac{a+b+c}{2}}\) とすると
$$S=\sqrt{s(s-a)(s-b)(s-c)}$$
では、上で解いた問題をヘロンの公式を用いてやってみましょう。
【問題】
\(△ABC\)において、\(a=4,b=3,c=2\)のとき、この三角形の内接円の半径の大きさを求めよ。
ヘロンの公式を用いて三角形の面積を求めます。
まずは準備として\(s\)の値を求めます。
$$s=\frac{4+3+2}{2}=\frac{9}{2}$$
そして、ヘロンの公式にそれぞれの値をあてはめます。
$$\begin{eqnarray}S&=&\sqrt{s(s-a)(s-b)(s-c)}\\[5pt]&=&\sqrt{\frac{9}{2}\left(\frac{9}{2}-4\right)\left(\frac{9}{2}-3\right)\left(\frac{9}{2}-2\right)}\\[5pt]&=&\sqrt{\frac{9}{2}\cdot \frac{1}{2}\cdot \frac{3}{2}\cdot \frac{5}{2}}\\[5pt]&=&\frac{3\sqrt{15}}{4}\end{eqnarray}$$
面積が求まったら、あとの手順は同じですね。
$$\begin{eqnarray}S&=&\frac{r}{2}(a+b+c)\\[5pt]\frac{3\sqrt{15}}{4}&=&\frac{r}{2}(4+3+2)\\[5pt]\frac{3\sqrt{15}}{4}&=&\frac{9}{2}r\\[5pt]r&=&\frac{3\sqrt{15}}{4}\cdot\frac{2}{9}\\[5pt]r&=&\frac{\sqrt{15}}{6}\cdots(解) \end{eqnarray}$$
とまぁ、こんな感じで
ヘロンの公式を使うと三角形の面積部分が簡単に求めれるようになります。
内接円の半径を求めたい場合には、ヘロンの公式もセットで覚えておくとよいですね!
いや、ヘロンの公式使っても計算大変そうだけど!
って思った方はスイマセンw
ヘロンの公式は、\(s\)が整数になるときにはすごくラクに計算ができるのでホント便利ですよ!
ちょっと問題のチョイスをミスったかな(^^;)
まとめ!

というわけで、内接円の半径を求めるためには上の公式をしっかりと覚えておきましょう!
忘れてしまった場合には、三角形を分割して合わせたものだ!という発想から自分で導けるようになると最高ですね(^^)
















コメントを残す