今回の記事では数Ⅰで学習するデータの分析の単元から
「四分位数とは何か」
について、超基礎の内容から解説していきます。
なんとなくは理解しているけどちょっと曖昧だなぁ…
という方はこの記事を通して理解を深めていきましょう(^^)
四分位数について中学生向けに解説した動画も作りました!
こちらも合わせてどうぞ(‘ω’)ノ
四分位数とは何か
四分位数(しぶんいすう)とは、データを大きさの順に並べたとき、4等分する位置の値のことをいいます。
4等分するためには、仕切りが3つ必要になりますね。
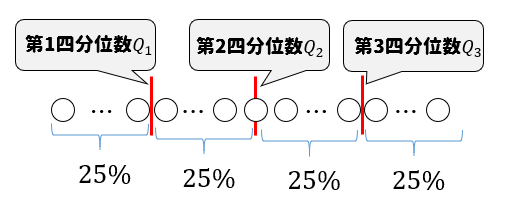
1番目の仕切りに位置する値のことを第1四分位数\(Q_1\)
2番目の仕切りに位置する値のことを第2四分位数\(Q_2\)(中央値)
3番目の仕切りに位置する値のことを第3四分位数\(Q_3\)といいます。
そして、第3四分位数と第1四分位数の差(\(Q_3-Q_1\))を四分位範囲といいます。
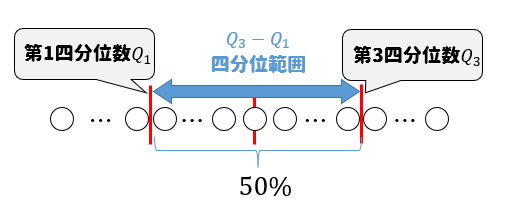
四分位範囲とは、真ん中に位置する50%がどれくらい散らばっているかを表しています。
そのため、データが中央値あたりにギュッと集まっている場合には四分位範囲は小さくなります。
つまり、四分位範囲からデータの散らばりのおおよその度合いを読み取ることができます。
そして、四分位範囲を半分にした値を四分位偏差といいます。
四分位数の求め方
では、例題を用いて四分位数を求める手順について確認してみましょう。
【例題】
次のデータについて、四分位数、四分位範囲、四分位偏差を求めなさい。
$$2,3,1,1,5,9,1,4,5$$
まずはデータを大きさの順に並べ替え、中央値を求めましょう。

中央値の値が第2四分位数となります。
中央値の求め方ってどうだっけ…という方はこちらの記事をご参考ください。
次に、第2四分位数を境にデータを前半、後半部分に分けます。

そして、前半と後半部分の中でそれぞれの中央値を求めましょう。
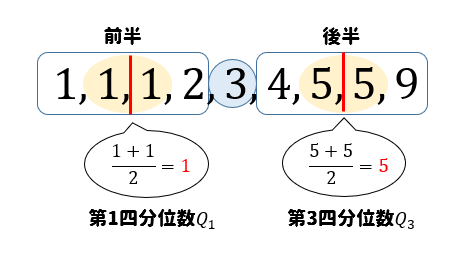
すると、それらが第1四分位数と第3四分位数となります。
次に四分位範囲を求めましょう。
第3四分位数と第1四分位数の差なので
$$Q_3-Q_1=5-1=4$$
となります。
四分位偏差は、四分位範囲を半分にしたものです。よって
$$\frac{4}{2}=2$$
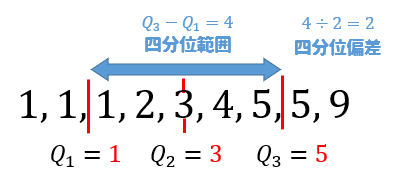
求める順としては次のようになりますね。
- 第2四分位数(中央値)を求める
- 第1四分位数、第3四分位数を求める
- 四分位範囲、四分位偏差を求める
【例題】
次のデータについて、四分位数、四分位範囲、四分位偏差を求めなさい。
$$3,3,7,1,6,5,8,9,1,5$$
それではこちらも同じように求めてみましょう。
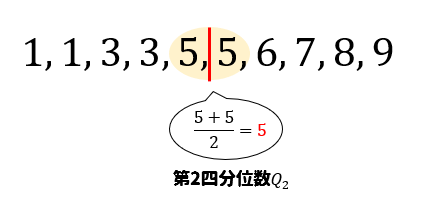
まずは第2四分位数を求める。
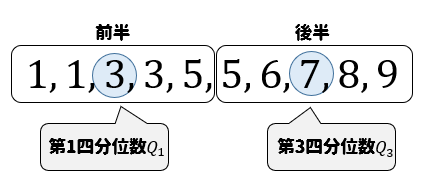
次に前半、後半部分に分けて第1四分位数と第3四分位数を求めましょう。
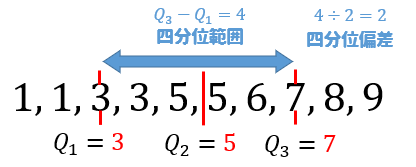
よって、四分位範囲は\(7-3=4\)、四分位偏差は\(4\div2=2\)となります。
四分位数は何番目?
では、ここではちょっとだけ発展的なお話もしておきましょう。
データの数が少ない場合には、順番を数えることで四分位数を調べることができました。
しかし、データが100個もあるようなときにはどうしますか?
数えていたら大変ですね…汗
こういうときには、四分位数が何番目にあるのか?
を素早く見極めれるようになるとラクになります。
というわけで、この章では四分位数は何番目?ということについて考えてみましょう。
【データが100個あるとき】
まずは第2四分位数(中央値)が何番目になるか考えてみます。
中央値は全体の数を2で割ると
\(100\div 2=50\)となるので、50と51番目の平均を見るということになります。
第2四分位数が求まったことで、前半は1~50、後半は51~100ということがわかりました。

次は、前半の1~50の中央値を求めることで第1四分位数が何番目になるかを考えます。
\(50\div 2=25\) となるので、第1四分位数は25番目と26番目の平均となります。
次は、後半の51~100の中央値を求めると第3四分位数が何番目になるかを考えます。
ここはスタートが51になっているので÷2で考えるのはちょっと複雑になっちゃいますね。
なので
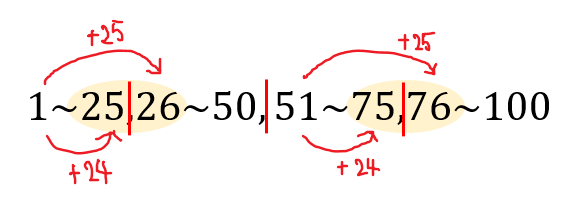
このように考えてみると分かりやすいです。
前半部分はスタートから+24、+25した部分が中央となるので、後半部分も同じようにスタートの51から+24、+25下部分を見ればよいです。
よって、まとめておくと
第1四分位数…25、26番目の平均
第2四分位数…50、51番目の平均
第3四分位数…75、76番目の平均
となります。
【データが101個あるとき】
中央値は全体の数を2で割ると
\(101\div 2=50.5\)となるので、51番目を見るということになります。
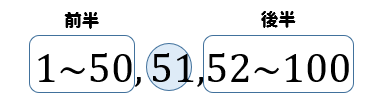
第2四分位数が求まったことで、前半は1~50、後半は52~101ということがわかりました。
次に前半1~50の中央値(第1四分位数)を考えてみましょう。
\(50\div2=25\)となるので、25、26番目の平均となります。
そして、後半52~101の中央値(第3四分位数)は次のようになります。

第1四分位数…25、26番目の平均
第2四分位数…51番目
第3四分位数…76、77番目の平均

まとめ!


というわけで、今回は四分位数についてサクッと解説しておきました。
データの分析の単元では難しそうな用語がたくさん出てきますが、意味することはとても単純だったりします。
今回の四分位数とは、データを4等分する仕切りに位置する値のことです。
最初の仕切りから順に第1四分位数、第2四分位数、第3四分位数といいます。
ここでは中央値を正確に求める力が必要となります。
中学数学の復習になりますが、不安な方はこちらの記事で復習しておいてくださいね!
さて、四分位数を理解できたら次は箱ひげ図ですね!















Great!
理解しやすい
super great