こんにちは!数スタの小田です。
今回は高校数学Ⅰで学習する三角比の単元から「正弦定理、余弦定理の使い分け」についてイチから解説します。
取り上げる問題はこちら!
【問題】次の値を求めなさい。
(1) \(a=2, b=\sqrt{6}, B=60°\)のとき、\(c\)
(2) \(a=3, b=\sqrt{3}, A=60°\)のとき、\(B\)
(3) \(A=135°, a=7\)のとき、外接円の半径\(R\)
(4) \(a=3, b=5, c=7\)のとき、\(C\)
さぁ、パッと見たときに正弦定理、余弦定理のどちらを使えばいいかわかりましたか??
「よぉわからんわ…」という方も今回の記事を最後まで読んでもらえれば、それぞれの見分け方について完璧に理解できるようになるのでがんばっていきましょう(‘ω’)ノ
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
正弦定理、余弦定理の見分け方
正弦定理のポイント
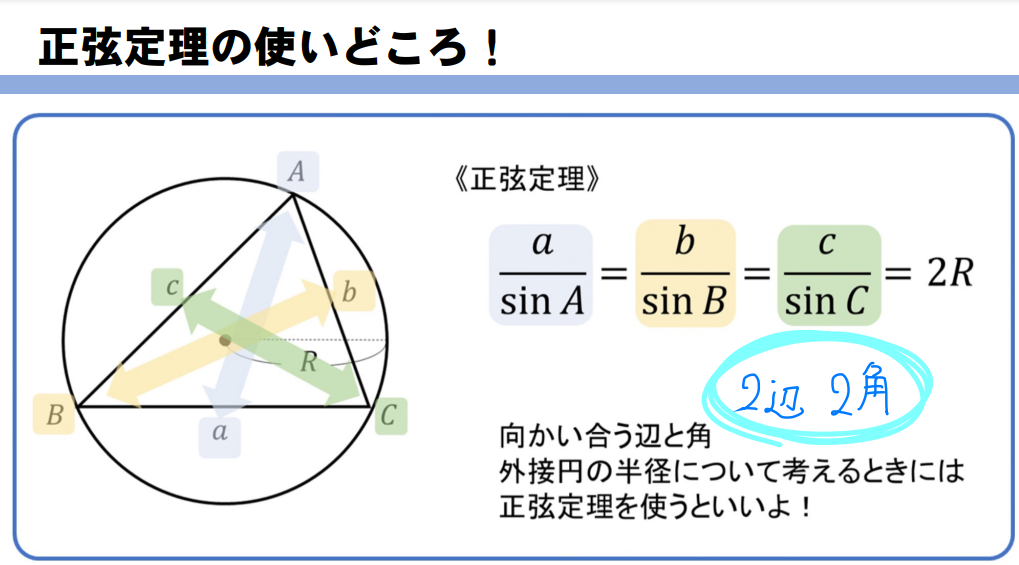
問題文から「向かい合う辺と角」「外接円の半径」が与えられたときには正弦定理を使います。
与えられた、求めたい辺と角が「2辺2角」のとき ⇒ 正弦定理を使う。
と考えることもできますね!
具体的には、こんな感じです。
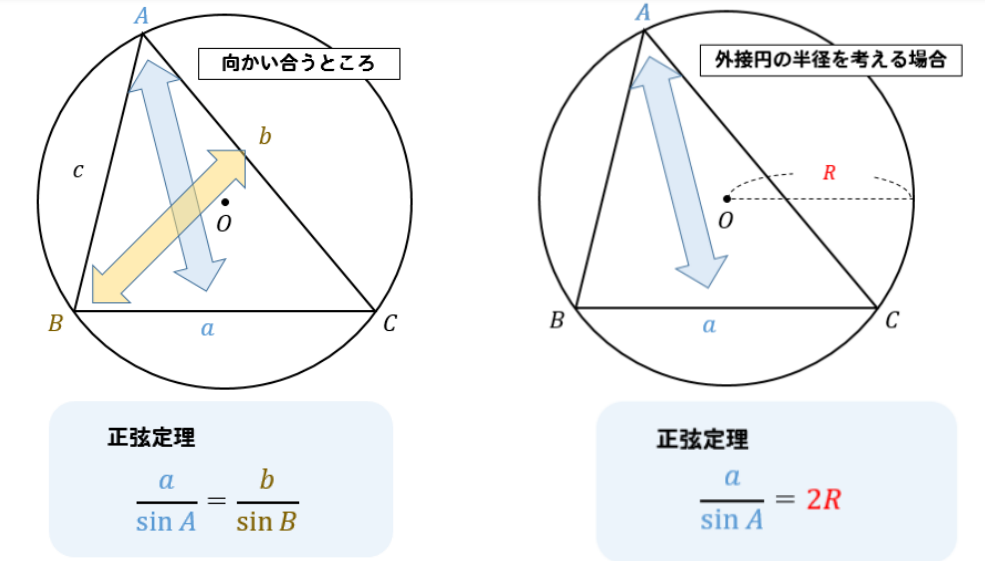
与えられた辺、角を図に書き込んでみて「向かい合うところに位置している」ときには上の画像のように正弦定理をとりましょう。
また、外接円がでてきたときには一発で正弦定理の出番だと判断できます^^
余弦定理のポイント
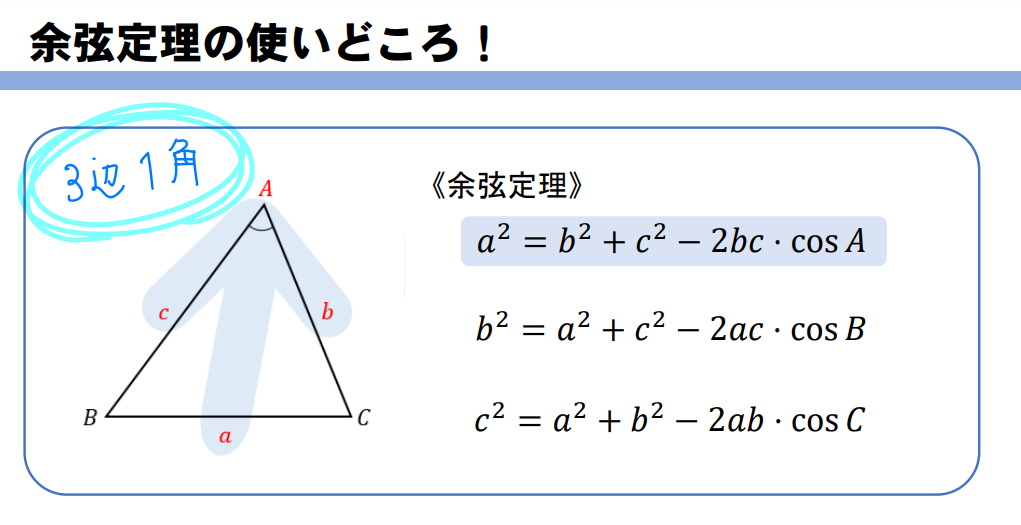
問題文から与えられた辺、角、求めたいところを書き込んでみたところ、上のような矢印型の位置関係になっているときには余弦定理の出番となります。
また、与えられた、求めたい辺と角が「3辺1角」のとき ⇒ 余弦定理を使う。
と考えることもできます!
それでは、問題を使って正弦、余弦定理の使い分けにチャレンジしてみましょう!
問題を使って使い分けにチャレンジ!
(1)の問題

必ずイメージ図をかくようにしてください。
そうすると、辺、角が矢印型の位置関係、または「3辺1角」の関係になっていることが読み取れます。
そのことから今回は余弦定理を使えばいいと判断できますね!
(2)の問題
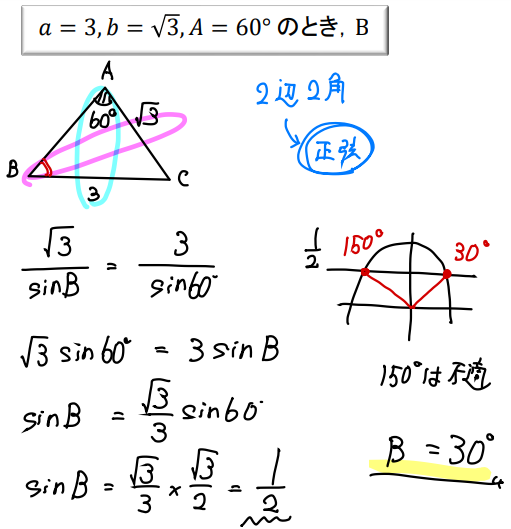
イメージ図を書いてみると、向かい合う辺と角の関係、または「2辺2角」の関係と読み取れます。
よって正弦定理の出番だと判断できますね!
(3)の問題
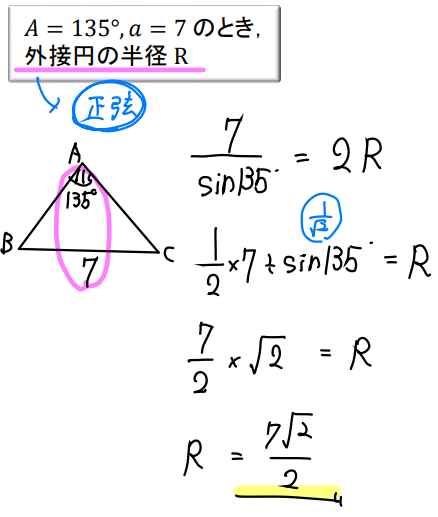
これは楽勝!
問題文に「外接円の半径」が出てきていることから、一発で正弦定理だと判断できますね^^
(4)の問題
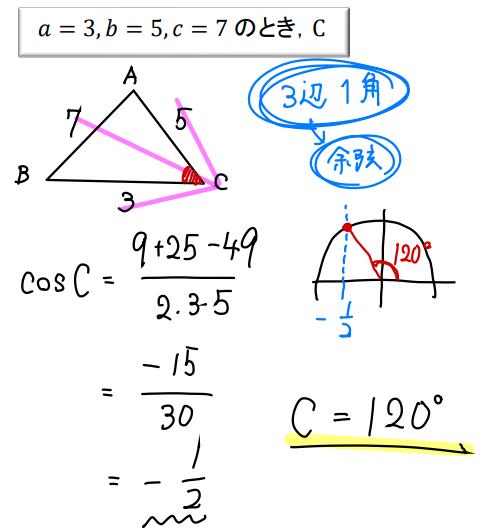
これもイメージ図を書いてみると矢印型、または「3辺1角」と読み取ることができるので、余弦定理の出番だと判断できます。
ここでは \(\cos{C}=\cdots\) の形で余弦定理を使っていますね。
この式についてはこちらの記事でも詳しく解説しているので参考にしてくださいね^^
まとめ
お疲れ様でした!!
どうかな?これで正弦定理、余弦定理の使い分けがバッチリになっていたら嬉しいな^^
大事なポイントとしては「しっかりイメージ図をかくこと」だと思っています。
問題文にある辺、角の大きさを眺めているだけでは分かりづらいです。
(というか、僕はそこだけで判断するのはムリ!!)
なので、しっかりと図をかいて、どういった位置関係になっているのかな?ってことを読み取るようにしてくださいね!
というわけで、
今回は以上!














コメントを残す