高校数学Ⅰで学習する三角比の単元から
「三角比の式の値」
について解説していきます。
取り上げる問題はこちら!
【問題】
\(\sin\theta+\cos\theta=\frac{1}{2}\) のとき,次の式の値を求めよ。ただし,\(0°≦\theta≦180°\) とする。
(1)\(\sin\theta \cos\theta\)
(2)\(\frac{\sin\theta}{\cos\theta}+\frac{\cos\theta}{\sin\theta}\)
(3)\(\sin\theta-\cos\theta\)
この問題を解くためには、三角比の相互関係を覚えておく必要があります。
- \(\sin^2\theta+\cos^2\theta=1\)
- \(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\)
- \(\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}\)
【参考記事】
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
(1)の解説!両辺を2乗する
\(\sin\theta+\cos\theta=\frac{1}{2}\) のとき,次の式の値を求めよ。ただし,\(0°≦\theta≦180°\) とする。
(1)\(\sin\theta \cos\theta\)
条件として、三角比の和、差が与えられたときには、
両辺を2乗すると突破口が見えてきます!
では、両辺を2乗するとどうなるか見ていきましょう。
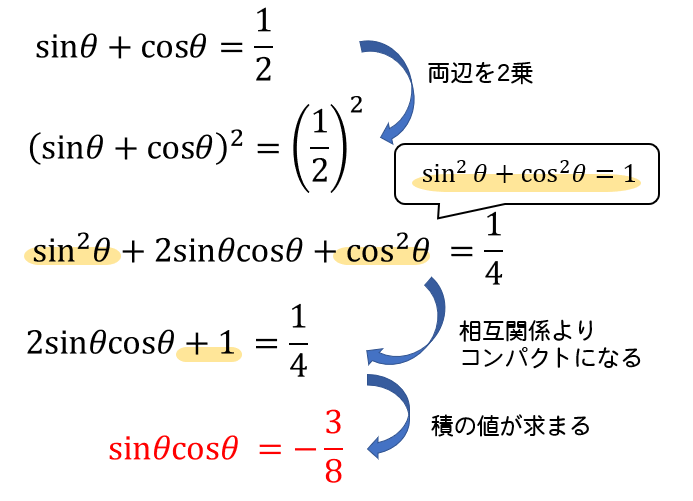
と、このように2乗することによって、三角比の積の値を求めることができます。
\(\sin^2\theta+\cos^2\theta=1\) という相互関係を覚えておく必要がありますが難しい変形ではありませんね。
三角比の和、差が与えられたら両辺を2乗することで積の値を求めることができる。
しっかりと覚えておいてくださいね(^^)

答え
$$\sin\theta\cos\theta=-\frac{3}{8}$$
これで(1)の答えが求まったわけなんだけど、
後の問題で必要になってくることなので、もう少しだけ深掘りしておきます。
今回の問題では、\(0°≦\theta≦180°\) となっていることから
\(\sin\theta\) は正であることが確定しています。
ですが、\(\theta\) が鋭角、鈍角どちらなのかがハッキリしていないため、\(\cos\theta\) の符号については明らかになっていません。
しかし!
(1)で \(\sin\theta\cos\theta\) の値を求めたことにより、
\(\cos\theta\) の符号が明らかになるのです!
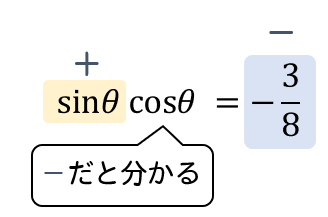
\(\sin\theta\) と \(\cos\theta\) の積が負になっていて、
\(\sin\theta\) が正であると分かっているのだから、
そこから \(\cos\theta\) の符号は負になるぞ!ってことが分かりますね。
\(\cos\theta\) が負になるという話は(3)を解くときに活用します。
(2)の解説!通分する
\(\sin\theta+\cos\theta=\frac{1}{2}\) のとき,次の式の値を求めよ。ただし,\(0°≦\theta≦180°\) とする。
(2)\(\frac{\sin\theta}{\cos\theta}+\frac{\cos\theta}{\sin\theta}\)
分数の加法なので、通分をして式をまとめていきます。
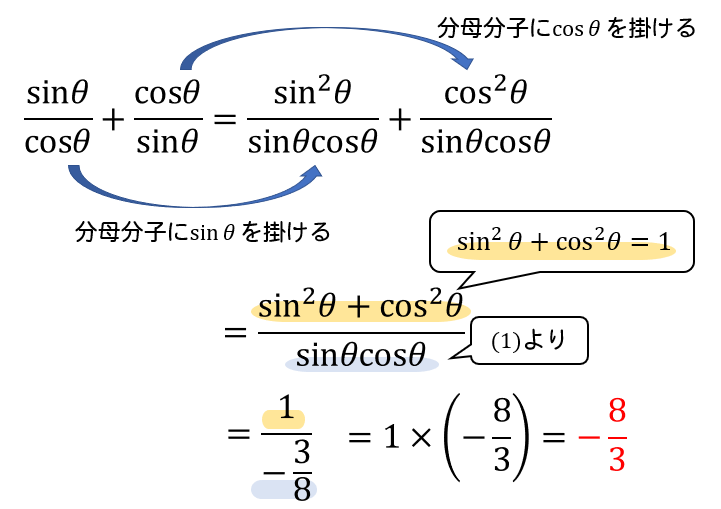
(1)の値を利用しながら解いていってくださいね!
答え
$$\frac{\sin\theta}{\cos\theta}+\frac{\cos\theta}{\sin\theta}=-\frac{8}{3}$$
(3)の解説!2乗と符号に注意!
\(\sin\theta+\cos\theta=\frac{1}{2}\) のとき,次の式の値を求めよ。ただし,\(0°≦\theta≦180°\) とする。
(3)\(\sin\theta-\cos\theta\)
差の値を直接求めるのは、ちょっと難しいです(^^;)
なので、遠回りのようになるのですが、
一旦、\((\sin\theta-\cos\theta)^2\) の値を求めます。
そして、その2乗の値の平方根を求めることによって \(\sin\theta-\cos\theta\) の値を明らかにしていきます。
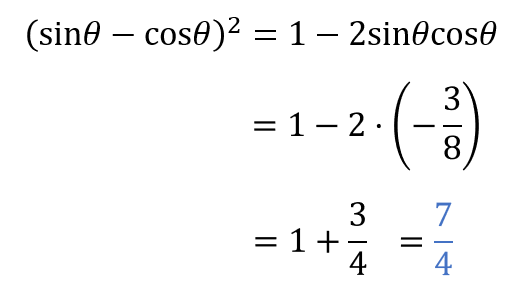
2乗の値が求まったので、次に平方根を考えていきます。
ですが、ここで注意するポイントがあります!
\(\sin\theta -\cos \theta\) の符号は正?負?
という点です。
そのまま平方根をとってしまうと、\(\sin\theta-\cos\theta=\pm\frac{\sqrt{7}}{2}\) となってしまいますが、+と-両方とも答えでいいのだろうか、どちらかは不適になるのだろうか。
この辺りをしっかりとチェックしておく必要があります。
さて!
ここで役に立つのが(1)で考えておいた\(\sin\theta, \cos\theta\) の符号になります。
今回の問題では、\(\sin\theta\) は正、\(\cos\theta\) は負であることが分かっています。
となると…
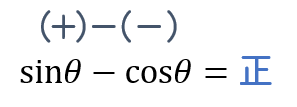
正の数から負の数を引くってことだから、\(\sin\theta-\cos\theta\) は正になるってことが分かりますね。
以上より、平方根を取るときには±ではなく、+の値だけを答えに選べばよいってことが判断できます。
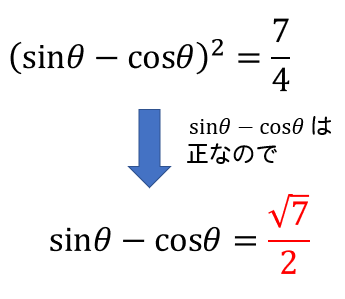
答え
$$\sin\theta -\cos\theta=\frac{\sqrt{7}}{2}$$
このように、\(\sin\theta-\cos\theta\) の値を求めるときには、いろんな注意すべき点があります。
- 直接求めるのが難しいから、まずは2乗の値を求める。
- \(\sin\theta-\cos\theta\)の符号に気を付けて、平方根の値を求める。
まとめ!
お疲れ様でした!
三角比の式の値は入試や模試などでよく見かける問題です。
和、差が与えられているときには両辺を2乗して積を求めることができる。
この考え方と式の変形について覚えておけば楽勝な問題です。
サクッと解けるように練習しておいてくださいね(/・ω・)/


















コメントを残す