次のような高さの分からない正四角錐
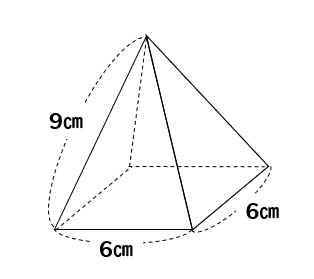
どうやって体積を求めたらよいのでしょうか??
これは、中3で学習する三平方の定理を用いて解いていきます。
高さの分からない正四角錐の体積を求める方法
【問題】
次の正四角錐の体積を求めなさい。
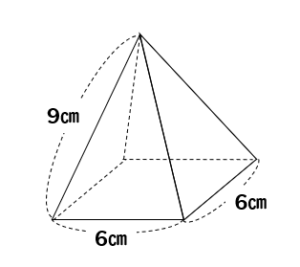
正四角錐の体積を求めるためには…

$$(体積)=(底面積)\times \color{red}{(高さ)}\times \frac{1}{3}$$
高さが必要になります。
なので、まずは正四角錐の高さを求めることから始めましょう。
最初に注目するのは底面の正方形です。
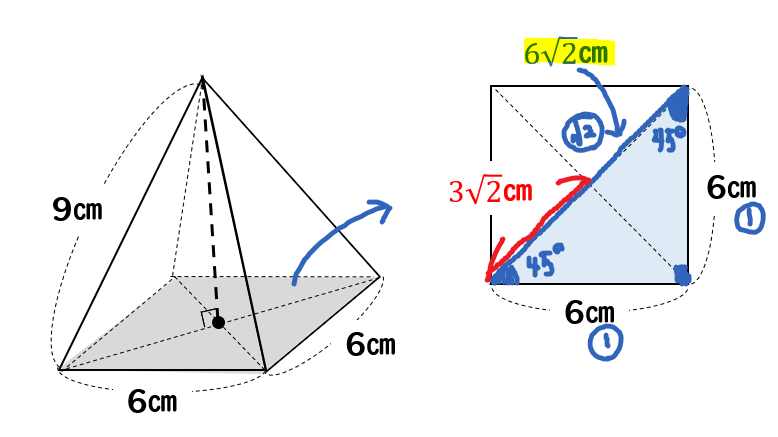
このように底面の対角線を引いて、その長さを求めます。
すると45°、45°、90°の直角三角形ができるので
\(1:1:\sqrt{2}\)の比になりますね。
そこから、対角線の長さは\(6\sqrt{2}cm\)
さらに、その半分の長さ\(3\sqrt{2}cm\)まで求めておきましょう。
次に、正四角錐の高さを含む
こちらの直角三角形に注目します。
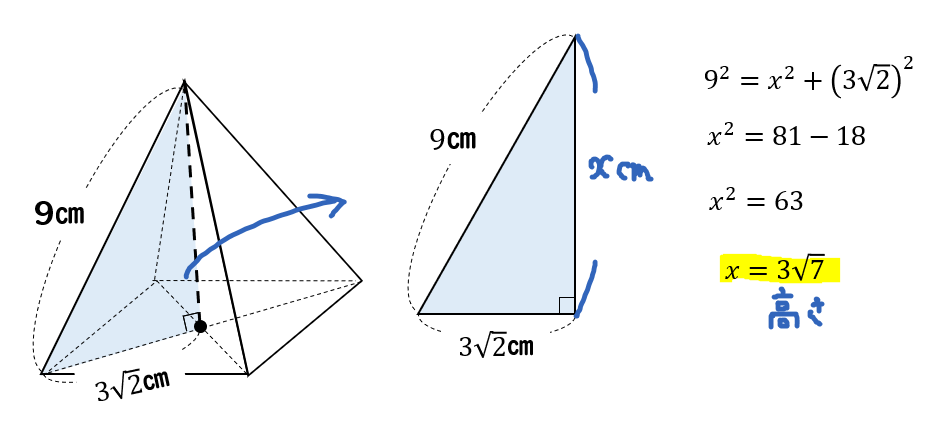
すると、先ほど求めた\(3\sqrt{2}㎝\)の辺を用いて
三平方の定理から高さを求めることができます。
ようやく正四角錐の高さが求まったので
あとは体積の公式に当てはめていけば完成ですね(^^)
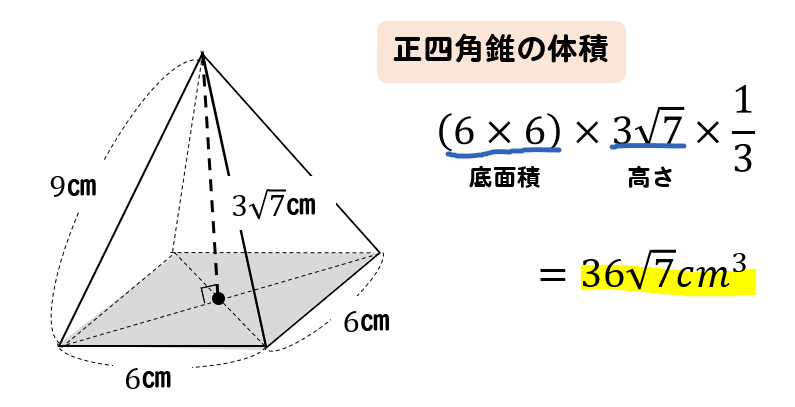
答え
$$36\sqrt{7}㎝^3$$
では、手順をまとめておきましょう。
正四角錐の体積の求め方
- 底面の正方形に注目。対角線の長さ、その半分の長さを求める。
- 正四角錐の高さを含む直角三角形に注目、三平方の定理から高さを求める。
- ②で求めた高さを用いて、体積の公式に当てはめて計算する。

練習問題に挑戦しよう!
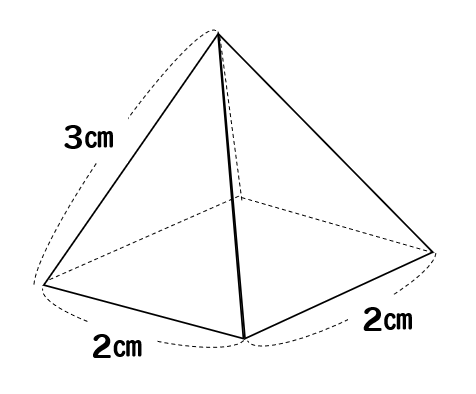
【問題】
次の正四角錐の体積を求めなさい。
まとめ!
お疲れ様でした!
正四角錐の高さが分からない場合には、
ちょっとめんどうではあるけど、今回紹介した手順を用いて計算をしていってください。
慣れてしまえば簡単に体積を求めれるようになるので頑張ってくださいね(/・ω・)/




















難しいです
頑張るべ!
ありがとうございます
お役に立てて良かったです^^
いいっすね
分母にルートが来た場合は有利化するのですか?
そうですね!
わかりやすい