今回は中3で学習する
『三平方の定理』
の利用問題について解説していくよ！
こんな問題見たことあるかな？
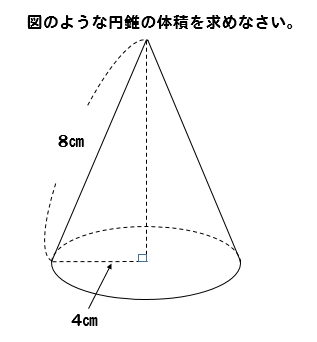
1年生のときによく出てきたような体積を求める問題なんだけど
今までとはちょっと違うような…
そうです！
高さが書いてありませんっ！！
高さが分からないのに
どうやって体積を求めればいいんだろう…
と、困ってしまう場面で
役に立つのが三平方の定理なのです。
それでは、解説していくよー！
三平方の定理の基礎については
こちらの記事を参考にしてくださいね(^^)
Contents
円錐の高さを求める方法！
それでは、どのように円錐の高さを求めればよいのかを解説していきます。
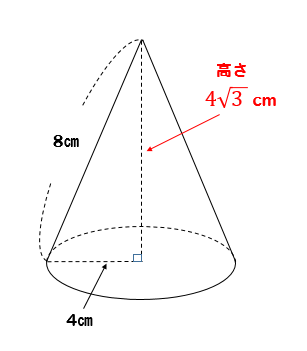
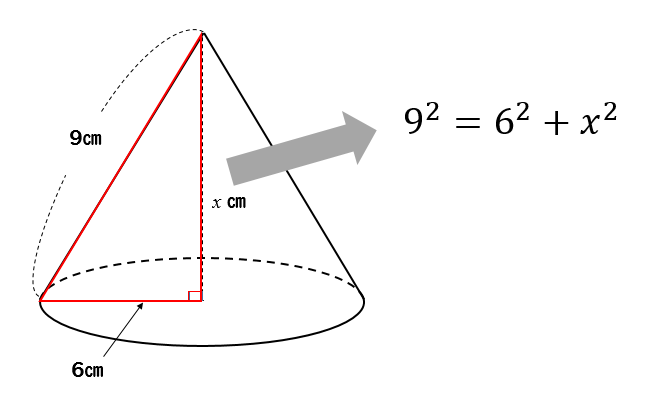
まずは、円錐の中から直角三角形を見つけます。
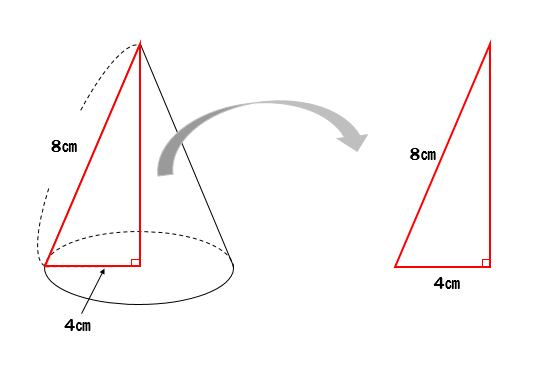
そして、三平方の定理を使って直角三角形の高さを求めれば
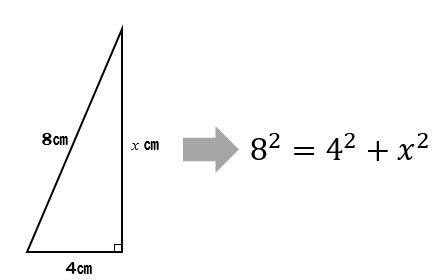
$$8^2=4^2+x^2$$
$$64=16+x^2$$
$$x^2=64-16$$
$$x^2=48$$
$$x=\pm 4\sqrt{3}$$
\(x>0\)だから
$$x=4\sqrt{3}$$
これで、円錐の高さを求めたことになります。
うーん…
めっちゃ簡単だった。
円錐の体積を求める！
高さがわかれば体積を求めることができますね。
円錐の体積の求め方を確認しておくと
こうでしたね。
コレに当てはめて考えていきましょう。
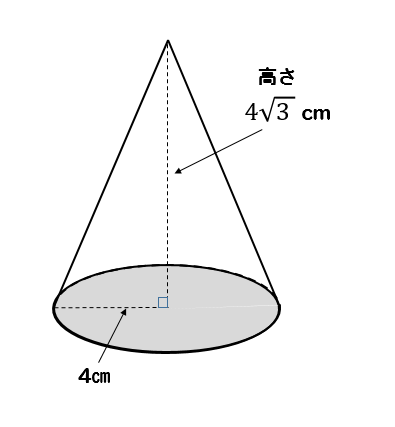
底面積は円の面積公式\(\pi r^2\)に当てはめて
$$\pi \times 4^2=16\pi$$
となるので、体積は
$$16\pi \times 4\sqrt{3} \times \frac{1}{3}$$
$$=\frac{64}{3}\sqrt{3}\pi cm^3$$
となりました。
三平方の定理を使って
高さを求めることができれば
あとは1年生で学習したことを使って求めることができます。
いくつか練習問題を用意しておきました。
理解を深めるために挑戦してみてください！
演習問題で理解を深める！
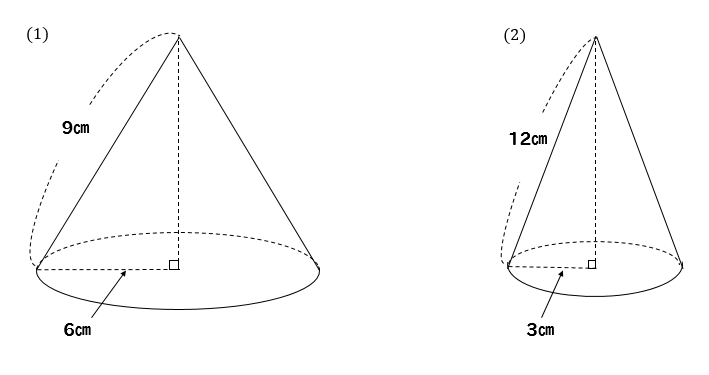
次のような立体の体積を求めなさい。
直角三角形を見つけて
三平方の定理から高さを求めます。
$$9^2=6^2+x^2$$
$$81=36+x^2$$
$$x^2=81-36$$
$$x^2=45$$
$$x=\pm 3\sqrt{5}$$
\(x>0\)だから
$$x=3\sqrt{5}$$
高さがわかれば、体積の公式に当てはめて計算していきます。
底面積は\(\pi \times 6^2=36\pi\)となるので
$$36\pi \times 3\sqrt{5} \times \frac{1}{3}$$
$$=36\sqrt{5}\pi$$
（1）答え
$$36\sqrt{5}\pi cm^3$$
直角三角形を見つけて
三平方の定理から高さを求めます。
$$12^2=3^2+x^2$$
$$144=9+x^2$$
$$x^2=144-9$$
$$x^2=135$$
$$x=\pm 3\sqrt{15}$$
\(x>0\)だから
$$x=3\sqrt{15}$$
高さがわかれば、体積の公式に当てはめて計算していきます。
底面積は\(\pi \times 3^2=9\pi\)となるので
$$9\pi \times 3\sqrt{15} \times \frac{1}{3}$$
$$=9\sqrt{15}\pi$$
（2）答え
$$9\sqrt{15}\pi cm^3$$
円錐の展開図パターン！
ここからは、ちょっとひねった問題を解説していきます。
やっていくことは同じなんだけで
いじわるな出題者は、ちょっと違った見方で問題を出してきます。
次のような展開図になる立体の体積を求めなさい。
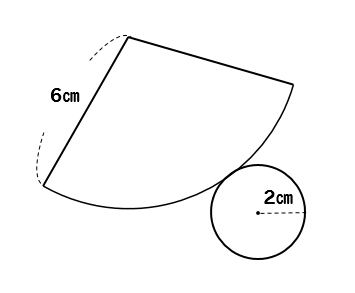
まさかの展開図！！
ですが、ここは落ち着いて
展開図を立体にしてやりましょう。
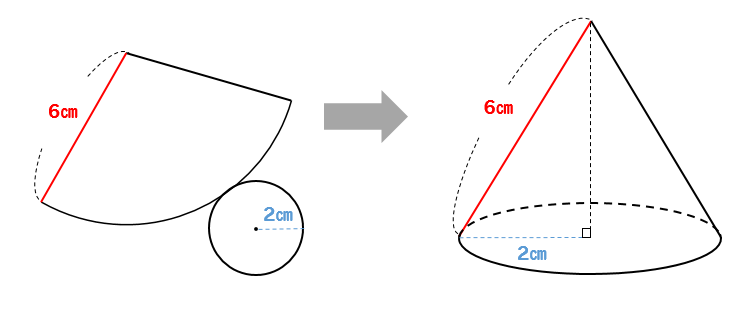
ここまで持ってくることができれば
今までの問題と同じだと考えることができますね。
展開図の場合、最初に組み立て作業が加わるだけで
全然難しくないからね！
答えを求めておくと
高さは
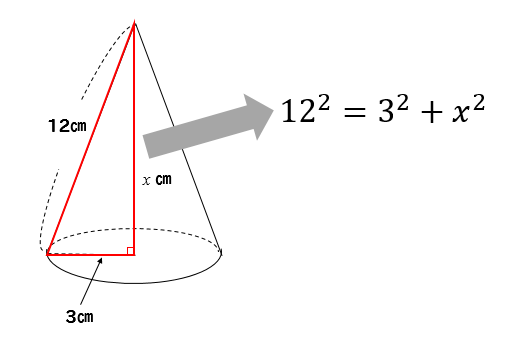
$$6^2=2^2+x^2$$
$$x=4\sqrt{2}$$
体積は
$$4\pi \times 4\sqrt{2} \times \frac{1}{3}$$
$$=\frac{16}{3}\sqrt{2}\pi cm^3$$
となります。
これで
展開図で出されても大丈夫ですね！
半径がわからないパターン
ここまでずっと
円錐の高さのことばかり言ってきましたが
次の立体の体積を求めなさい。
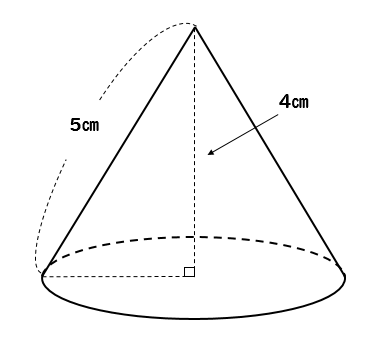
このように半径がわからなくなっているパターンもあります。
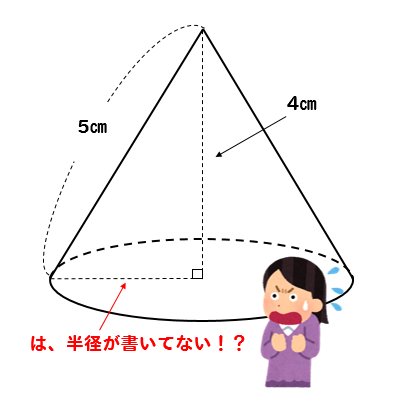
この場合でも、やることは同じです。
円錐の中から直角三角形を見つけて
三平方の定理を利用して半径を求めます。
$$5^2=x^2+4^2$$
$$x^2=9$$
$$x=3$$
半径がわかれば
底面積を求めて
$$\pi \times 3^2=9\pi$$
体積の公式に当てはめて
$$9\pi \times 4 \times \frac{1}{3}$$
$$=12\pi cm^3$$
となります。
半径がわからない場合でも
考え方は、高さを求めるときと同じですね！
円錐の体積を求める方法 まとめ
お疲れ様でした！
円錐の体積を求めるときに
高さや半径がわからない場合
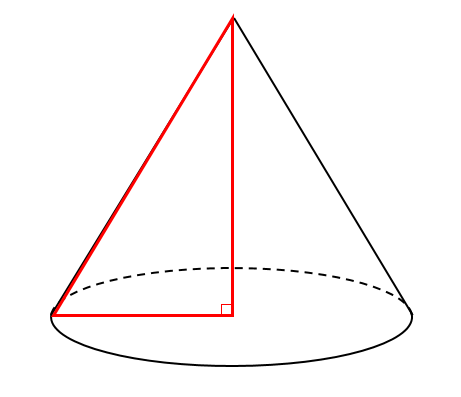
このように直角三角形を見つけて
三平方の定理を利用することで
わからないところの長さを求めるようにしましょう！
コレで円錐の体積問題はこわくないぞ！
どんどん問題に挑戦していこう。
ファイトだー(/・ω・)/
円錐の高さが？？体積を求める問題を解説！←今回の記事
高校入試で使える公式集をプレゼント！
高校入試で使える公式をまとめた教材を作成しました！
定期テスト、入試で高得点を取るためには絶対に知っておきたいものばかりを集めています。
学校では教えてくれないような公式もありますよ(/・ω・)/
これは知らないと損をするかも…！？
無料の中学生メルマガ講座にご登録いただいた方に、
高校入試で使える公式集をプレゼントさせていただいております。
こちらから公式集を無料で手に入れちゃってください！
ご登録いただいたメールアドレスに教材を送らせていただきます。
登録は1分もあれば完了します。
ぜひ、こちらから中学生メルマガ講座に登録してみてくださいね(^^)
コメントを残す