今回は『三平方の定理』から
方程式を利用する発展問題を解説していきます。
高さがわからない三角形の面積問題
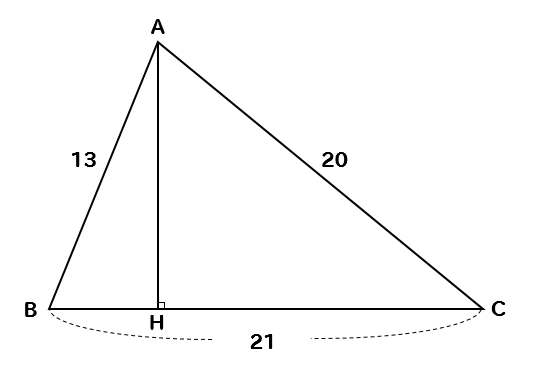
△ABCの面積を求めなさい。
図形の折り返し問題
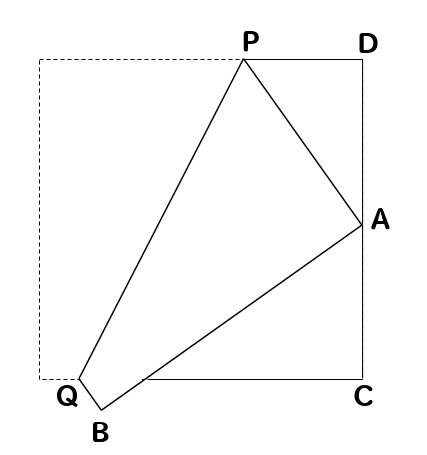
1辺の長さが6㎝の正方形の紙ABCDを、頂点Aが辺CDの中点にくるように折り、折り目を線分PQとしたものです。線分PDの長さを求めなさい。
高さがわからない三角形の面積問題を解説！
△ABCの面積を求めなさい。
この問題では、三角形の高さが与えられていません。
面積を求めるためには、まず高さを求める必要があります。
BHの長さを\(x\)とすると
CHの長さは\(21-x\)と表すことができます。
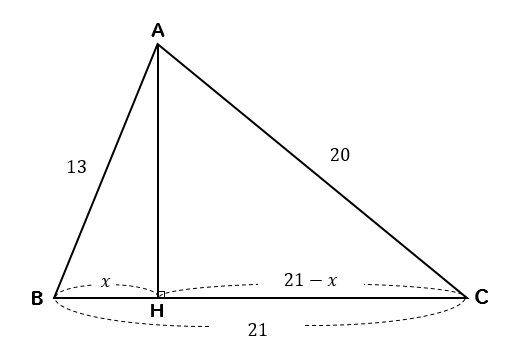
次に△ABHと△ACHに着目すると
それぞれ直角三角形になっているので
三平方の定理を利用することができます。
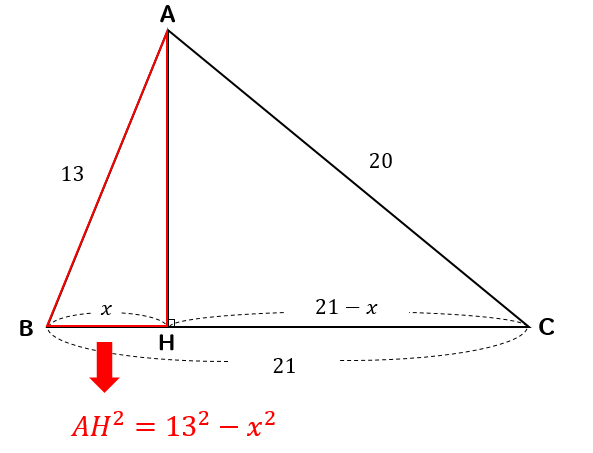
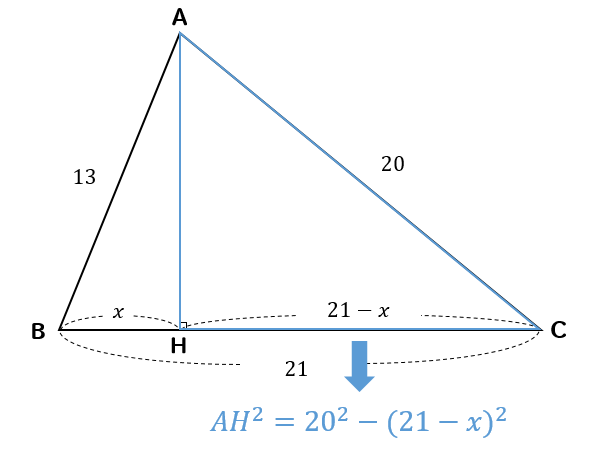
すると、それぞれ
$$AH^2=13^2-x^2$$
$$AH^2=20^2-(21-x)^2$$
と表すことができます。
この2つの式を連立方程式とみて計算すると
\begin{eqnarray} \left\{ \begin{array}{l} AH^2=13^2-x^2 \\ AH^2=20^2-(21-x)^2 \end{array} \right. \end{eqnarray}
\(AH^2\)が等しいので、代入法で解くと
$$13^2-x^2=20^2-(21-x)^2$$
$$169-x^2=400-(441-42x+x^2)$$
$$-x^2+x^2-42x=400-441-169$$
$$-42x=-210$$
$$x=5$$
\(x\)の値がわかったところで
\(AH^2=13^2-x^2\)に代入してやると
$$AH^2=13^2-5^2$$
$$AH^2=169-25$$
$$AH^2=144$$
$$AH=\pm 12$$
\(AH>0\)だから
$$AH=12$$
このようにして
三角形の高さを求めることができました。
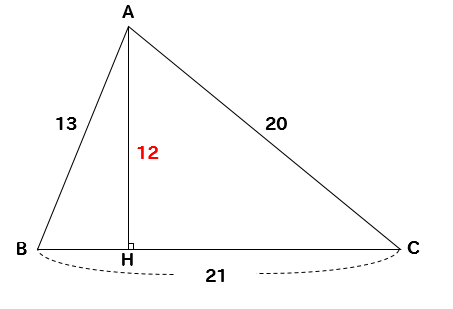
よって、三角形の面積は
$$21\times 12 \times \frac{1}{2}=126 $$
答え
$$126$$
高さがわからない三角形では
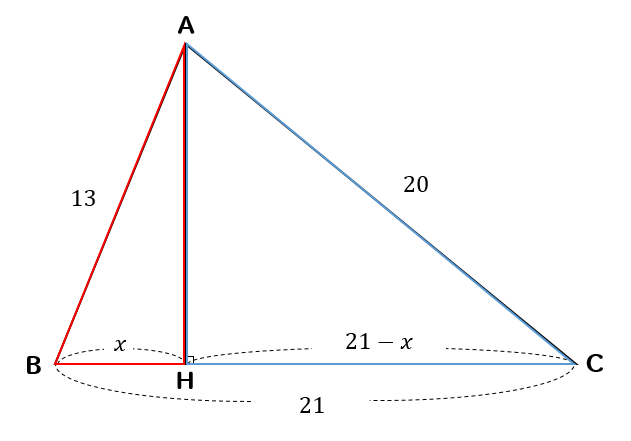
このように直角三角形を2つ作り
それぞれの底辺を\(x\)を用いて表す。
そして、三平方の定理を用いて方程式を作る。
これが解法手順になります。
文字で置くというのが大切だね
文字を使う勇気を持とう！！
図形の折り返し問題の解説！
1辺の長さが6㎝の正方形の紙ABCDを、頂点Aが辺CDの中点にくるように折り、折り目を線分PQとしたものです。線分PDの長さを求めなさい。
次は図形の折り返し問題です。
まずは、求めたいPDの長さを\(x\)とします。
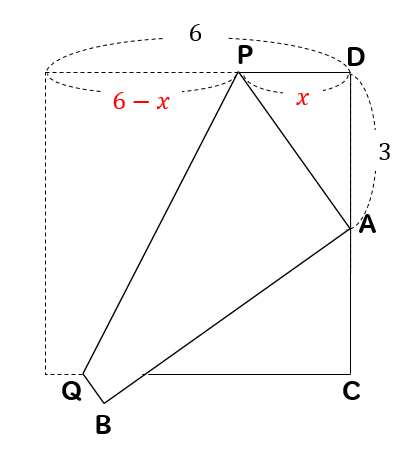
すると、PDのとなり部分は\(6-x\)と表すことができます。
そして、折り返し図形の特徴として
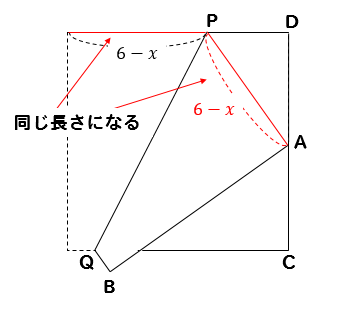
ここの部分の長さが等しくなります。
よって、PAの長さも\(6-x\)となります。
折り返される前にPAがいた位置だから
長さが等しくなるっていうのはイメージが湧くよね！
すると、次は直角三角形である△PADに注目すると
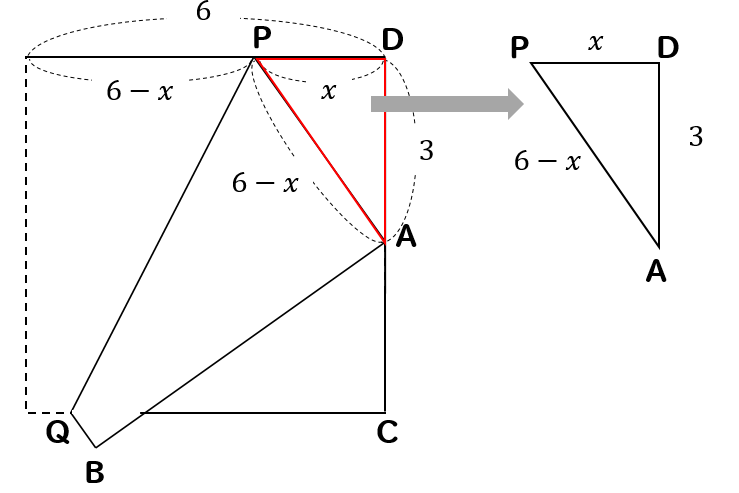
三平方の定理を用いることができるので
$$(6-x)^2=x^2+3^2$$
という式を作ることができます。
あとは、この方程式を解いていきます。
$$36-12x+x^2=x^2+9$$
$$-12x=-27$$
$$x=\frac{9}{4}$$
答え
$$\frac{9}{4} cm$$
図形折り返し問題のポイントは
どこが同じ長さになるのか？
折れ目を軸に対称になっているので
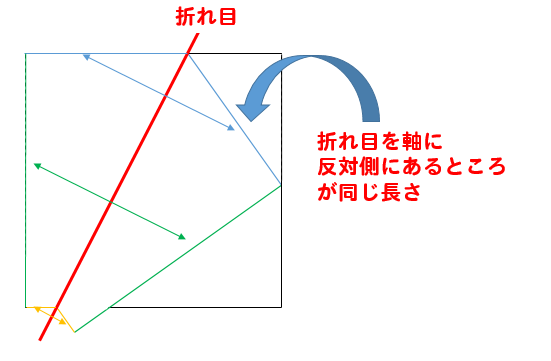
折れ目に注目して、探してみると見つけやすいですね！
三平方の定理 発展問題まとめ
お疲れ様でした！
入試などの発展問題では、今回のように
三平方の定理を使って、方程式を作ることで
長さを求めていくようになります。
まずは、求めたい部分を\(x\)とする。
直角三角形の各辺を\(x\)を使って表すことができれば
三平方の定理を使って、方程式を作る。
このような流れになります。
図形の中に直角三角形があれば
三平方の定理…かもな。
と、頭の中に入れておきましょう！
方程式を利用する発展問題を解説！←今回の記事
中学生向けの英文法サイトを開設！
≫ 中学英語の文法まとめサイト！