【中学数学】ひもの長さが最短になるのはどんなとき？？

今回は中3で学習する三平方の定理の単元から

「ひもの長さが最短になるのは？？」

という問題についてサクッと解説します。

 

こんな問題のことですね！

 

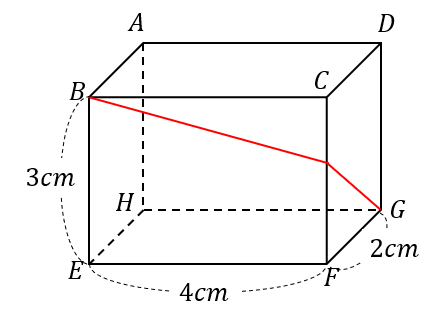
パッと見では難しそうな問題ですが、

ポイントをおさえておけば楽勝だぜ★

ひもの長さが最短になるのはどんなとき？？

 

 

では、こちらの問題の解き方を確認していきましょう。

空間図形のままでは、ひもの長さを考えるのが難しいです。

なので、ひもが通っているところの展開図を書いて、

平面で考えていきます。

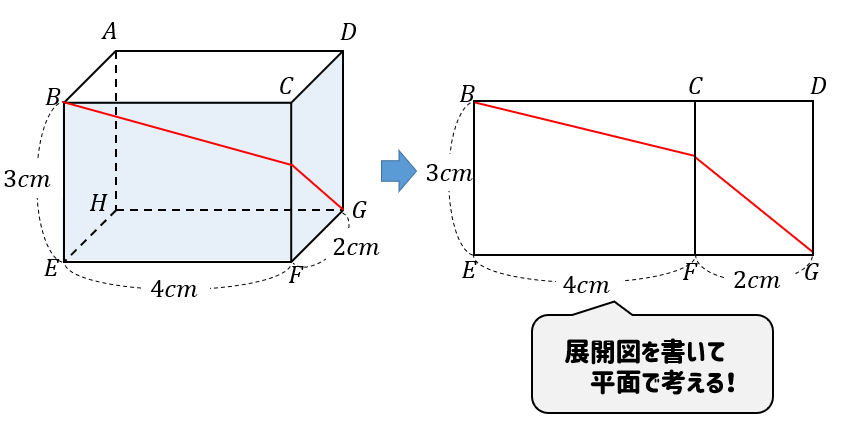
すると、ひもの長さっていうのも考えやすくなりますね(^^)

 

そして、ひもが最短になるというのは…

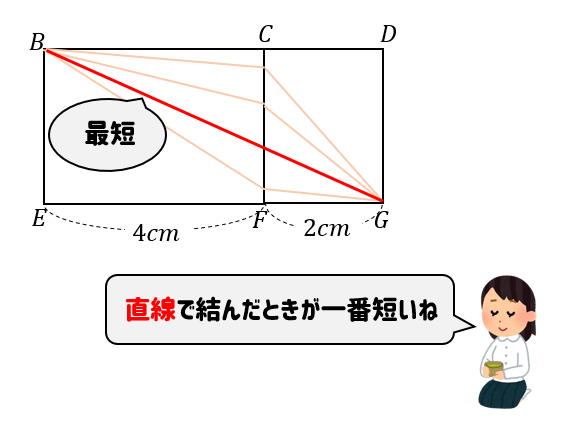
このように点と点を直線で結んだときの長さになります

 

よって、ひもが最短になる長さとは

展開図を書いたときのBGの長さと同じってことですね！

 

このことが理解できたら

あとは、三平方の定理を使って長さを求めていきましょう。

 

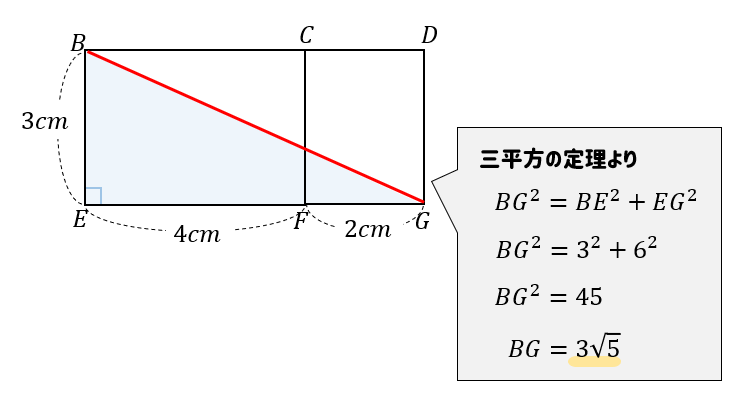
よって、ひもが最短となる長さは\(3\sqrt{5}cm\)となりました。

 

ひもが最短になる問題。

これのポイントは、展開図を書いて直線で結んだときの長さと等しい。

っていうことですね(^^)

このことをしっかりと覚えておきましょう。

 

では、他のパターンの例題を見て確認しておきましょう。

円錐のパターンも確認しておこう！

 

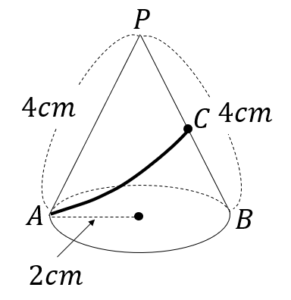
円錐のときも同じように展開図を書いて考えます。

ですが、円錐の場合には展開図を書くにあたって

側面であるおうぎ形の中心角を求める必要があります。

 

中心角の求め方は、こちらの裏ワザ公式を利用すると簡単ですね(^^)

＞円錐の表面積、中心角を求める問題を丁寧に解説！

 

今回の問題では、中心角は…

$$\frac{2}{4}\times 360=180°$$

となります。

 

よって、展開図はこんな感じ。求める長さは赤線の部分となります。

 

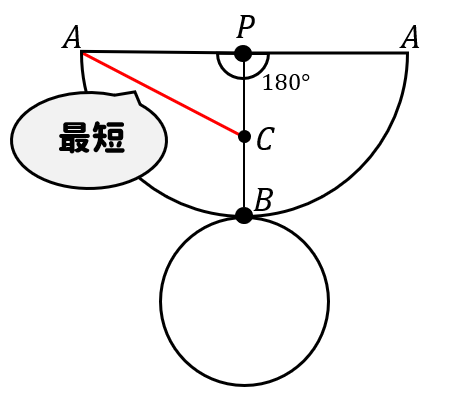
よって、三平方の定理を使って次のように長さを求めていきましょう。

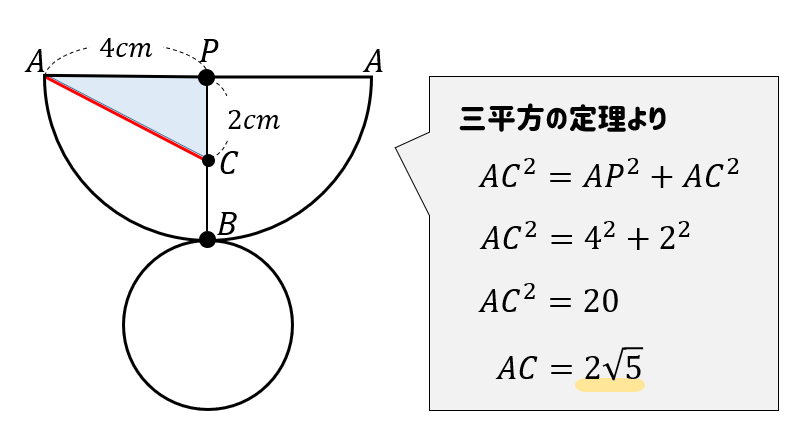
よって、ひもが最短となる長さは\(2\sqrt{5}cm\)となりました。

 

円錐の場合には、展開図を書くために側面であるおうぎ形の中心角を求める必要があります。

中心角の大きさによって展開図の形が大きく異なってくるので注意ですね！

まとめ！

お疲れ様でした！

ひもが最短となる問題を考えるときには…

展開図を書いて、直線で結ぶ！

これが大切なポイントとなります。

 

このことをしっかりとおさえておいて

たくさん問題を解きながら理解を深めていってくださいね(/・ω・)/