【三平方の定理】正三角形の高さ、面積を求める方法を解説！

今回の記事では

正三角形の高さと面積の求め方について解説していくよ！

ここでは、中３で学習する三平方の定理という知識を利用していきます。

三平方の定理があいまいな方は、まずはこちらの記事で確認しておいてくださいね(^^)

【三平方の定理】覚えておきたい基本公式を解説！

正三角形の高さと面積の求め方

正三角形の高さと面積を求める手順は以下の通りです。

それでは次の正三角形の高さと面積を

手順通り求めていきましょう！

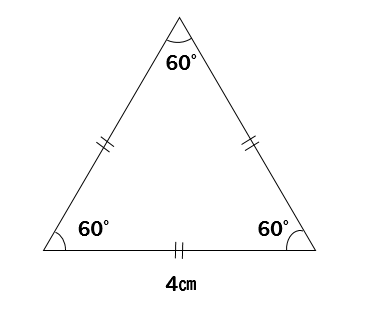
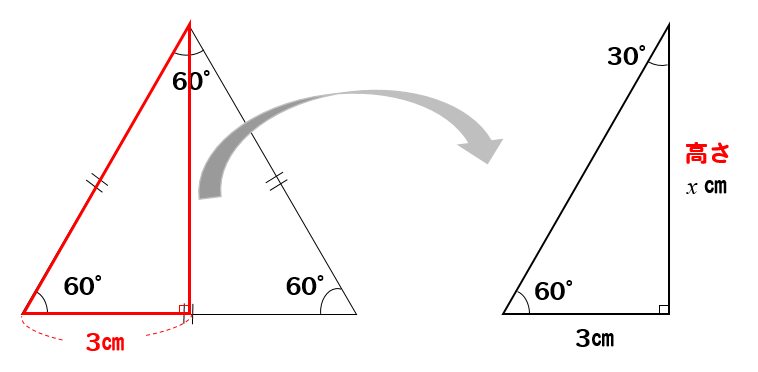
手順①　正三角形を半分にする

まず、正三角形を半分にすると

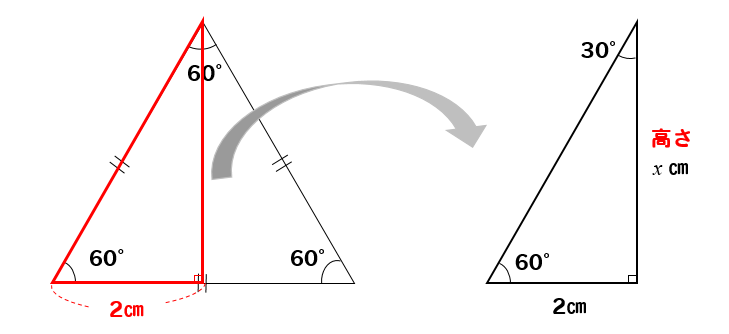
底辺部分は、長さが半分の\(2cm\)となり

30°、60°、90°の直角三角形ができあがります。

この三角形の高さが正三角形の高さと等しい

と考えることができますね。

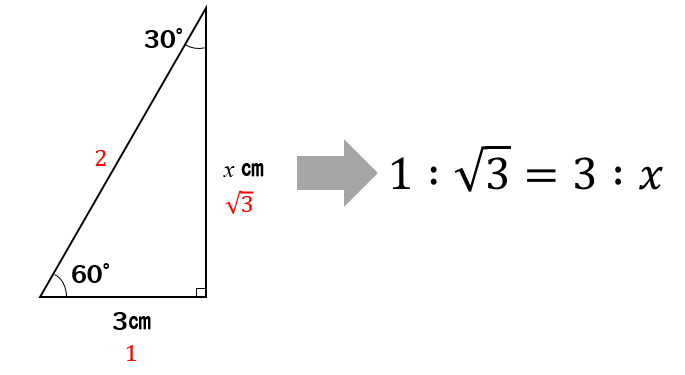
手順②　直角三角形の比を使って高さを求める

それでは、先ほど作った三角形の辺の比をとって

高さを求めてやりましょう。

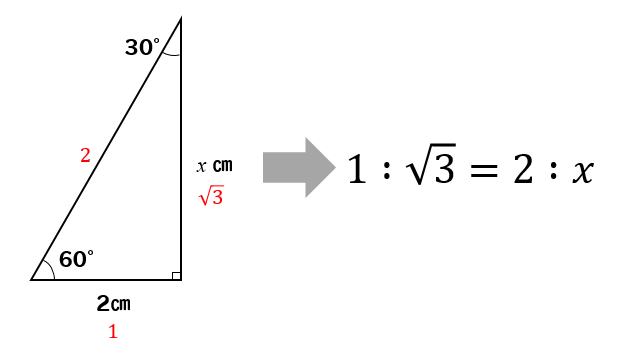
$$1:\sqrt{3}=2:x$$

$$x=2\sqrt{3}$$

このようにして、正三角形の高さを求めることができます。

手順③　高さを利用して面積を求める

三角形の面積の求め方は

$$（底辺）×（高さ）×\frac{1}{2}$$

これに当てはめて計算していくと

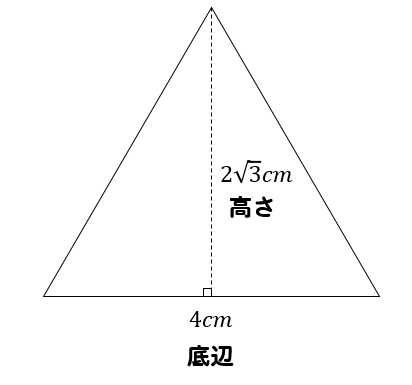
$$4\times 2 \sqrt{3} \times \frac{1}{2}$$

$$=4\sqrt{3}  cm^2$$

となります。

以上が正三角形の高さ、面積を求める手順でした。

特に難しいことはありませんでしたね(^^)

最後に1問、練習をして知識を固めておきましょう。

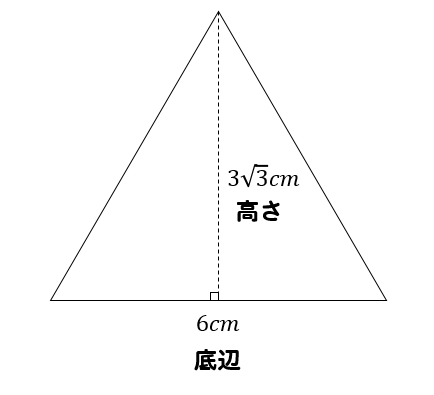
演習問題で理解を深める！

解説＆答えはこちら

$$9\sqrt{3} cm^2$$

まずは正三角形を半分にします。

 

次に、三角形の比をとって高さを求めると

 

$$1:\sqrt{3}=3:x$$

$$x=3\sqrt{3}$$

 

高さが求まったら

三角形の面積公式に当てはめて計算していきましょう。

 

$$6\times 3\sqrt{3}\times \frac{1}{2}$$

$$=9\sqrt{3}  cm^2$$

となります。

正三角形の高さ、面積の求め方　まとめ

お疲れ様でした！

正三角形の高さ、面積の求め方は

そんなに難しくありませんでしたね(^^)

三平方の定理が必要になってくるので

中学三年生にならないと出会うことのない問題だとは思いますが

入試にはすっごく出てくる問題なので、しっかりとマスターしておきたい！

いろんな長さの正三角形で

ちゃんと手順通り計算できるかどうか練習してみてね

ファイトだー(/・ω・)/