今回は『三平方の定理』という単元を
基礎から解説していきます。
三平方の定理は、いつ習う？
学校によって多少の違いはありますが
大体は3年生の3学期に学習します。
中3の終盤に学習するにも関わらず
入試にはバンバンと出題されてきます。
入試に出てきたけど
習ったばかりで理解が浅かった…
と、ならないように
早めに学習して理解を深めておきましょうね。
では、三平方の定理の基本公式
解説していくよ～！
Contents
三平方の定理とは
三平方の定理とは、直角三角形において
斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。
というものです。
文章だけでは、難しく見えますが
非常に単純な定理です。
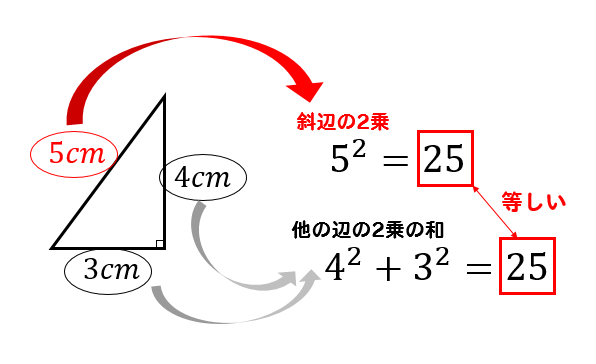
このように
斜辺の2乗の数と
他の辺を2乗して足した数が等しくなるのです。
直角三角形であれば、必ずこうなります。
では、この定理を使うと
どんな場面で役に立つかというと
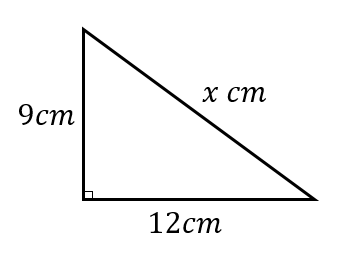
このように
直角三角形の2辺の長さがわかっていて
残り1辺の長さを求めたいときに本領を発揮します。
三平方の定理に当てはめてみると
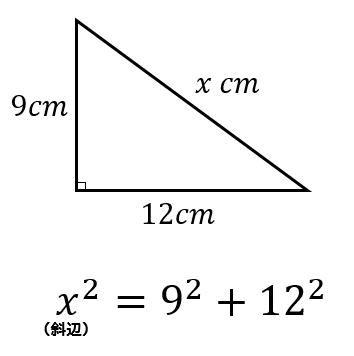
このような関係の式が作れます。
あとは、この方程式を解いていきましょう。
$$x^2=9^2+12^2$$
$$x^2=81+144$$
$$x^2=225$$
$$x=\pm 15$$
\(x>0\)なので
(長さを求めてるんだからマイナスはありえないよね)
$$x=15$$
このようにxの長さは15㎝だと求めることができました！
めちゃめちゃ便利な公式だよね
長さを調べるのに、ものさしがいらないなんて！
それでは、三平方の定理に慣れるために
いくつかの練習問題に挑戦してみましょう。
演習問題で理解を深める！
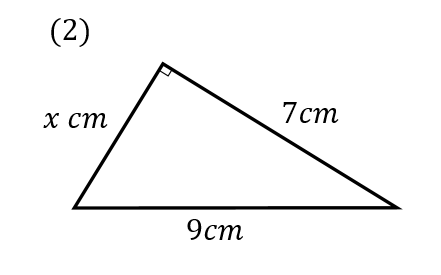
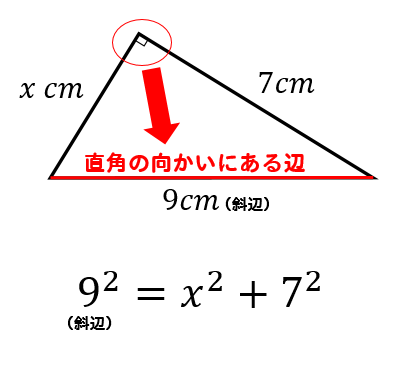
次の図のxの値を求めなさい。
三平方の定理に当てはめてみると
あとは計算あるのみ
$$x^2=6^2+8^2$$
$$x^2=36+64$$
$$x^2=100$$
$$x=\pm 10$$
\(x>0\)なので
$$x=10$$
（1）答え
$$10cm$$
こちらも三平方の定理に当てはめていくのですが
斜辺の場所に、ちょっと注意です。
斜辺は直角の向かいにある辺のことだからね！
斜辺は斜めになっている辺…と覚えてしまうと
ワケがわからなくなってしまうから気を付けてね。
では、あとは方程式を解いていきましょう。
$$9^2=x^2+7^2$$
$$81=x^2=49$$
$$x^2=81-49$$
$$x^2=32$$
$$x=\pm \sqrt{ 32 }$$
$$x=\pm 4\sqrt{2}$$
\(x>0\)なので
$$x=4\sqrt{2}$$
（2）答え
$$x=4\sqrt{2}$$
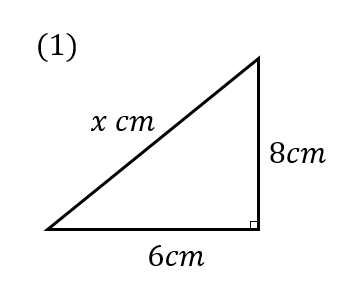
特別な直角三角形
では、三平方の定理はもうバッチリかな？
この単元では、直角三角形がメインとして扱われているんだけど
そんな直角三角形の中でも
特別な存在として君臨するものがあります。
それがコイツら！
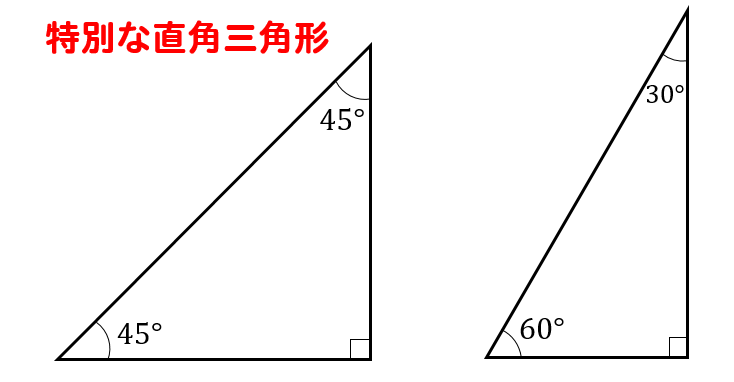
三角定規として使ってきた三角形ですね。
なぜコイツらが特別扱いをされているかというと
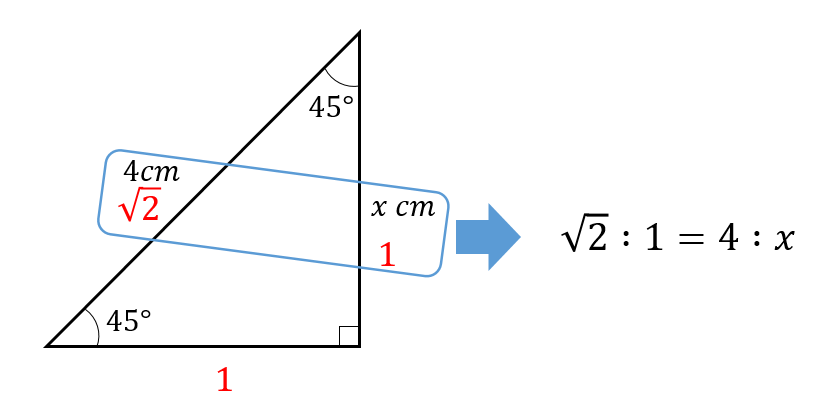
このような辺の長さの比になることがわかっているんですね。
辺の長さの比がわかるということは
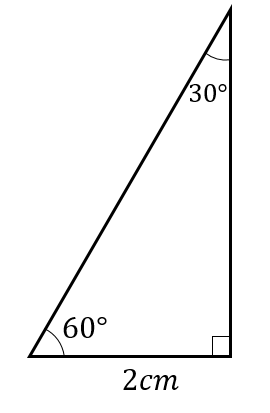
このように1辺だけでも長さが分かれば
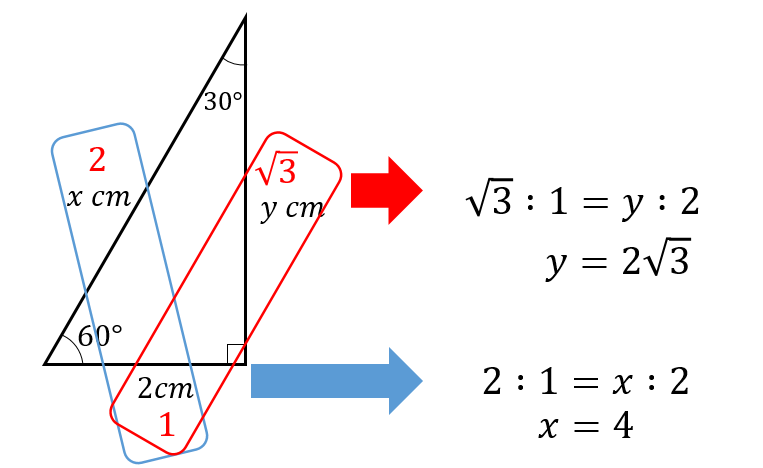
比をとってやることで
残り2辺の長さを求めることができます。
もちろん
\(1:1:\sqrt{2}\)や\(1:2:\sqrt{3}\)という比は覚えておく必要があるからね。
しっかりと覚えておこう！
では、特別な直角三角形において
比を使いながら辺の長さを求める練習をしていきましょう。
演習問題で理解を深める！
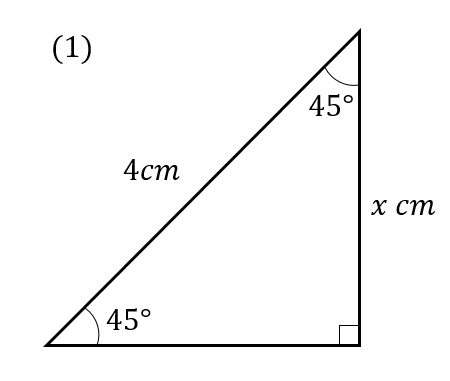
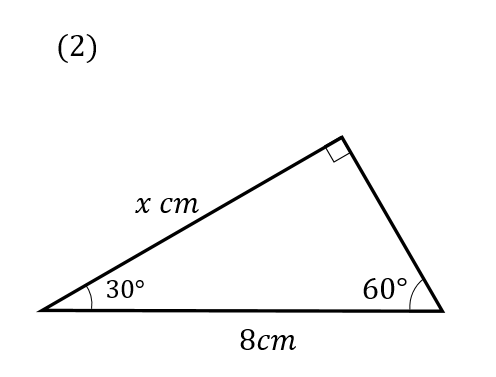
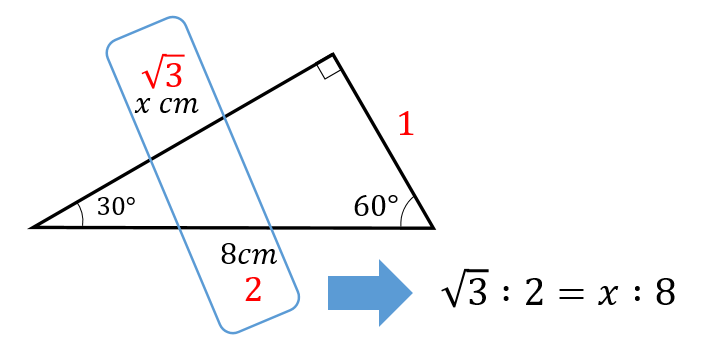
次の図のxの値を求めなさい。
45°、45°、90°の直角三角形の比は
\(1:1:\sqrt{2}\)でしたね。
辺の比を利用して式を作って計算していきます。
$$\sqrt{2}:1=4:x$$
$$\sqrt{2}x=4$$
$$x=\frac{4}{\sqrt{2}}$$
$$x=\frac{4\sqrt{2}}{2}$$
$$x=2\sqrt{2}$$
（1）答え
$$x=2\sqrt{2} cm$$
30°、60°、90°の直角三角形の比は
\(1:2:\sqrt{3}\)でしたね。
辺の比を利用して式を作って計算していきます。
$$\sqrt{3}:2=x:8$$
$$2x=8\sqrt{3}$$
$$x=4\sqrt{3}$$
（2）答え
$$x=4\sqrt{3} cm$$
三平方の定理 基本公式まとめ
お疲れ様でした！
これで三平方の定理の基本はバッチリです。
三平方の定理とは
直角三角形の長さを求めることができる便利な定理です。
そして、直角三角形の中には
特別な存在の三角形があります。
これらの直角三角形では、辺の比を利用して長さを求めることができます。
さぁ、三平方の定理はここからがスタートです！
新たな問題がどんどんと出てくるので
いろんな状況での利用の仕方を学んでいきましょう！
ファイトだー(/・ω・)/
初めに覚えておきたい三平方の基本公式！←今回の記事
成績を上げて、志望校合格を勝ち取りたい中3生の方！
数スタの無料メルマガ講座で合格を勝ち取りませんか？
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ わからないを解決！質問対応サポート
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
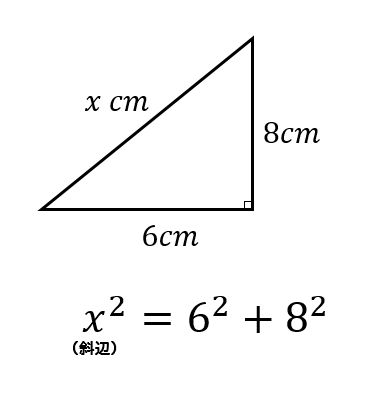
コメントを残す