【三平方の定理の逆ってなに？】どうやって証明するの？

三平方の定理とは、次のようなものでしたね。

【三平方の定理】覚えておきたい基本公式を解説！

これに対して、三平方の定理の逆とは？？

そもそも、なぜそんなことが成り立つの？証明方法は？

という点について解説していきます。

最後は、問題も用意しているので、この記事を通して三平方の定理の逆について理解を深めていきましょう！

Contents

三平方の定理の逆ってなに？
三平方の定理の逆を証明する
三平方の定理の逆を使った問題
2学期からでも最短で結果を出す！遅れを取り戻して一気に入試レベルまで引き上げる新講座
三平方の定理の逆【まとめ】

三平方の定理の逆ってなに？

三平方の定理を文字で起こしてみるとこんな感じ。

3辺の長さ $a, b, c(斜辺)$ とする直角三角形ならば、$c^2=a^2+b^2$ が成り立つ

これを逆にしたものを

3辺の長さが$a, b, c$の三角形において $c^2=a^2+b^2$ が成り立つならば、△ABCはcを斜辺とする直角三角形となる。

これを三平方の定理の逆といいます。

簡単にいうと…

3つの辺を見比べて

$$(一番長い辺)^2=(他の辺)^2+(他の辺)^2$$

が成立するならば、その三角形は直角三角形になるぜ！ってことだね。

ちょっと具体例を見てみましょう。

【例題】次の長さを3辺とする三角形は直角三角形になるかどうか答えなさい。

$$3cm, 4cm, 5cm$$

この中で一番長い辺は5㎝です。

他の長さが3㎝、4㎝ですね。

$$(一番長い辺)^2=5^2=25$$

$$(他の辺)^2+(他の辺)^2=3^2+4^2=25$$

よって、$(一番長い辺)^2=(他の辺)^2+(他の辺)^2$ が成り立ってる！

ってことが分かるよね。

だから、三平方の定理の逆より

直角三角形になるということがいえます。

【例題】次の長さを3辺とする三角形は直角三角形になるかどうか答えなさい。

$$7cm, 8cm, 9cm$$

この中で一番長い辺は9㎝です。

他の長さが7㎝、8㎝ですね。

$$(一番長い辺)^2=9^2=81$$

$$(他の辺)^2+(他の辺)^2=7^2+8^2=113$$

よって、$(一番長い辺)^2=(他の辺)^2+(他の辺)^2$ が成り立たない！

だから、この三角形は直角三角形ではありません。

このように、三平方の定理の逆を用いると3辺の長さからその三角形が直角三角形になるかどうかを調べることができるというわけです。

便利ですね～♪

ここからは高校生になってから学習すると思いますが

3辺の長さが次のような関係になっている場合

$c^2=a^2+b^2$ ⇒ 直角三角形

$c^2>a^2+b^2$ ⇒ 鈍角三角形

$c^2<a^2+b^2$ ⇒ 鋭角三角形

このように、3辺の長さからいろんな三角形の形を判断することもできます。

マメ知識として頭に入れといてください(^^)

三平方の定理の逆を証明する

三平方の定理の逆って、なんで成り立つの？証明はどうすんの？ってことをお話していきます。

3辺の長さが$a, b, c$の三角形において $c^2=a^2+b^2$ が成り立つならば、△ABCはcを斜辺とする直角三角形となることを証明せよ。

まずは、$c^2=a^2+b^2$ が成り立っている三角形を作ります。

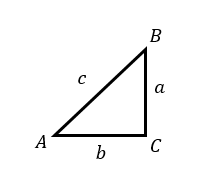
これに対して、辺の長さ$a, b$ をもち、その間の角が直角となる三角形を作ります。

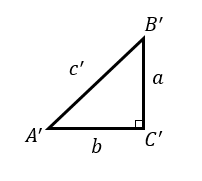
このときにできる斜辺の長さを$c’$とすると、直角三角形なので三平方の定理より

$$c’^2=a^2+b^2$$

が成立します。

仮定より、$c^2=a^2+b^2$ だから

$$c^2=c’^2$$

$c>0, c’>0$ なので、$c=c’$ ということが分かります。

そうなると、２つの三角形は3辺の長さがそれぞれ等しいので合同だということが判明！

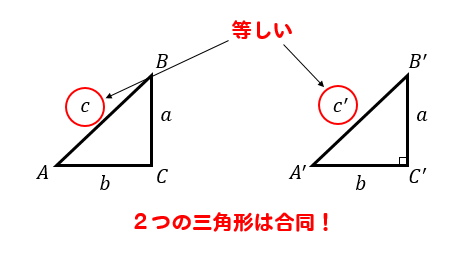
三角形が合同ということは、対応する角の大きさも等しい。

つまり、$∠C=∠C’=90°$ となります。

以上より

$c^2=a^2+b^2$ ならば $∠C=90°$ となることが証明できました！

つまり、△ABCはcを斜辺とする直角三角形になるということが分かりましたね。

三平方の定理の逆を使った問題

【例題】次の長さを3辺とする三角形は直角三角形になるかどうか答えなさい。

$$2cm, 3cm, 4cm$$

解説＆答えはこちら

答え

直角三角形にならない

この中で一番長い辺は4㎝です。

他の長さが2㎝、3㎝ですね。

$$(一番長い辺)^2=4^2=16$$

$$(他の辺)^2+(他の辺)^2=2^2+3^2=13$$

よって、$(一番長い辺)^2=(他の辺)^2+(他の辺)^2$ が成り立たない！

【例題】次の長さを3辺とする三角形は直角三角形になるかどうか答えなさい。

$$2cm, 3cm, \sqrt{5}cm$$

解説＆答えはこちら

答え

直角三角形になる

この中で一番長い辺は3㎝です。

他の長さが2㎝、$\sqrt{5}$㎝ですね。

$$(一番長い辺)^2=3^2=9$$

$$(他の辺)^2+(他の辺)^2=2^2+(\sqrt{5})^2=9$$

よって、$(一番長い辺)^2=(他の辺)^2+(他の辺)^2$ が成り立つ！

【例題】次の長さを3辺とする三角形は直角三角形になるかどうか答えなさい。

$$\sqrt{5}cm, \sqrt{7}cm, 2\sqrt{3}cm$$

解説＆答えはこちら

答え

直角三角形になる

この中で一番長い辺は$2\sqrt{3}$㎝です。

他の長さが$\sqrt{5}$㎝、$\sqrt{7}$㎝ですね。

$$(一番長い辺)^2=(2\sqrt{3})^2=12$$

$$(他の辺)^2+(他の辺)^2=(\sqrt{5})^2+(\sqrt{7})^2=12$$

よって、$(一番長い辺)^2=(他の辺)^2+(他の辺)^2$ が成り立つ！

2学期からでも最短で結果を出す！遅れを取り戻して一気に入試レベルまで引き上げる新講座

2学期に入り、入試が目前に迫ってきました。

「模試の点数が下がってしまった…」

「このままで大丈夫なのか…入試への不安が大きくなってきた」

「ウチの子がなかなか本気になってくれない」などなど

受験に対する悩みは尽きないですよね(^^;)

夏休みの施策が上手くいき、成績をガツンと伸ばすことに成功した方はこの調子でがんばっていけばOK！

一方で、現状の成績に不安を感じている、夏の遅れを取り戻したい…と感じている方は、

「入試過去問」×「王道パターン」×「動画」

この3つの要素を組み合わせた学習法を取り入れてみましょう。

そうすることで、ここからでも短期間でも成績を伸ばすことが可能です！

僕が教えてきた生徒さんの中でもこの学習法を取り入れることで、

2学期の時点で偏差値40前半

↓

入試本番で70点をクリア！（おそらく偏差値55くらい）

このような劇的UPを達成しているんですよ＾＾

ニガテな数学でこれだけ点を伸ばすことができれば、すっごく余裕ができますよね！

他にも次のような効果を実感することができます。

ニガテな数学がどんどん解けるようになって、勉強に自信がつく！他教科もがんばれるようになる。

動画を使ってお子さん1人でも学びを完結できる。親は見守っているだけで勝手に成長、点を伸ばしていく！

やったところがテストに出るので、遠回りすることなく最短で点数UPにつながる！次の模試で効果を実感できるかも！

塾に通わせなくても自宅だけで完結！時間、労力、費用を節約しながら効率よく合格をつかみとる！

受験だけでなく、高校進学後にも活きる数学の土台ができあがる！

今回はそんな「入試過去問」×「王道パターン」×「動画」という効率よく点数を伸ばしていく3要素を取り入れた教材を用意しました。

それがこちらです！