今回は「流水算」という計算のやり方についてイチから解説していきます。
流水算とは、中学受験でよく出題されるほか、就職試験などに活用されるSPIにも頻出の問題です。
川の流れが…静水時には…上りが下りが…
などなど
解答者を困惑させる言葉が盛りだくさんです(^^;)
だけど、流水算を解くためのポイントをおさえておけば
だれでも簡単に解けるようになっちゃう★
というわけで!
今回の記事では、流水算を解くために必要となるポイントをイチから解説していきます。
流水算のポイント(公式)
流水算の問題を解くためには、上り下りという考え方を身につけておく必要があります。
川には流れの向きがあります。
このように川は上から下に向かって流れていくよね。
この流れに沿って下に進むことを下りといいます。
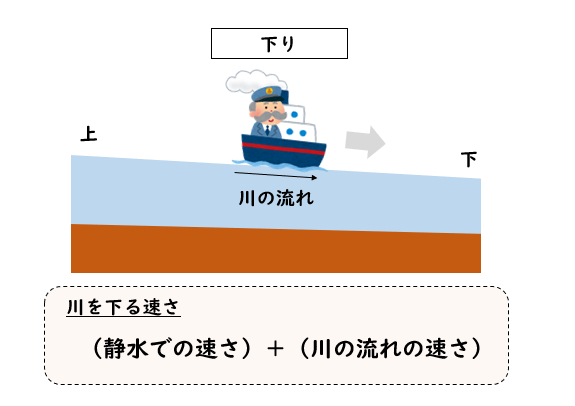
川を下るときには、川の流れが船を押してくれるので、いつもより速く進むことができます。
逆に、流れとは反対側に進むことを上りといいます。
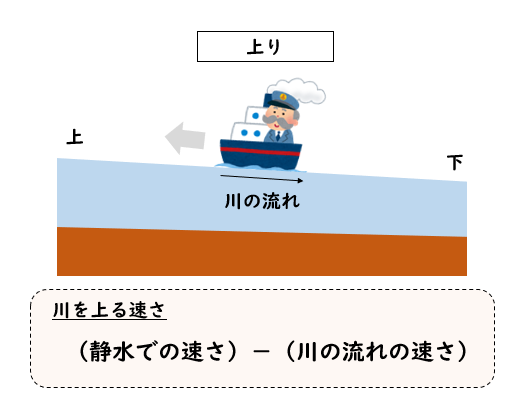
川を上るときには、川の流れが船を押し戻そうとするので、いつもより進むのが遅くなってしまいます。
このことを具体例でみておきましょう。
〈例題〉
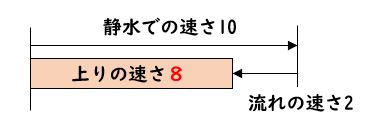
船の静水時の速さが時速10㎞、川の流れの速さが時速2㎞だった場合の上りと下りの速さはそれぞれいくらになるか求めましょう。
上りの速さは、静水時の速さから川の流れを引けばよいので
$$[上り] 10-2=時速8㎞$$
下りの速さは、静水時の速さに川の流れを足せばよいので
$$[下り] 10+2=時速12㎞$$
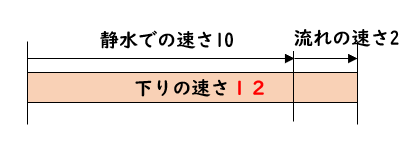
このようにそれぞれ求めることができます。
さらに踏み込んで考えてみましょう。
上りと下りの速さを見比べてみると…
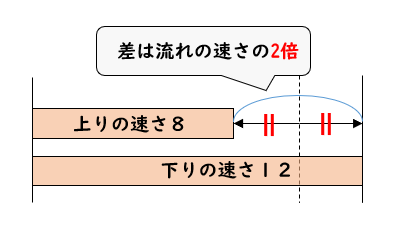
上りと下りの差は、川の流れの速さの2倍になっていることがわかりますね!
なので、次の問題のように上り、下りの速さから川の流れの速さを求めることもできちゃうわけですね。
〈例題〉
上りの速さが時速20㎞、下りの速さが時速26㎞のとき、川の流れの速さを求めましょう。
上りと下りの差は \(26-20=6\) であり、差の半分が川の流れの速さになるので
$$(26-20)\div 2=3$$
よって、川の流れの速さは時速3㎞となります。
下りの速さ
(静水時の速さ)+(川の流れの速さ)
上りの速さ
(静水時の速さ)ー(川の流れの速さ)
川の流れの速さ
(下りの速さ ー 上りの速さ)÷2
では、これらのポイントをおさえた上で流水算の問題を解いてみましょう!
流水算の問題解き方
流水算の基本問題
まず、45㎞の川を下るのに3時間かかったということから下りの速さを求めましょう。
速さを求めるためには、(道のり)÷(時間)を計算すればよかったですね。
下りの速さは、\(45\div 3=時速15㎞\) ということがわかります。
下りの速さは、静水時の速さに川の流れの速さを加えたものだったから

川の流れの速さは、\(15-12=時速3㎞\) ということがわかりました。
すると、川を上るときの速さが求めれます。
$$12-3=時速9㎞$$
上りのときには、45㎞の川を時速9㎞の速さで進むことになるので時間は
$$45\div 9=5時間$$
ということになります。
答え
5時間
うん、まぁ、難しくないね!
上り、下り、川の流れの関係を理解しておけば簡単に解くことができます(^^)
では、どんどんと問題を見ていきましょう。
差を利用して考える
まずは、川を上るとき、下るときの速さをそれぞれ求めましょう。
$$[上り] 24\div 3=時速8㎞$$
$$[下り] 24\div 2=時速12㎞$$
上りと下りの速さの差の半分が川の流れの速さになるんでしたね!

ということから、川の流れの速さは
$$(12-8)\div 2=時速2㎞$$
となります。
川の流れの速さが求まれば、静水時の速さは簡単!
下りの速さから流れの速さを引く
上りの速さに流れの速さを足す
どちらの方法でも構わないので、これらを計算することで求めれます。
$$[静水時] 8+2=時速10㎞$$
答え
【静水時】時速10㎞ 【川の流れの速さ】時速2㎞
流水算(中学受験問題)
速さを遅くする
さすが中学受験問題!
かなりややこしいですね(^^;)
だけど、落ち着いて1つずつ解決していきましょう。
まずは、川の流れの速さを求めたい!
ってことで、上りのときの速さを求めると \(24\div 5=時速4.8時間\) ということがわかります。
これより、川の流れの速さは、\(5-4.8=時速0.2時間\) となります。
次に、下りのときについて考えます。
下りでも同じく5時間かかったということから、上りと同じ速さ(時速4.8時間)で進んでいたことがわかります。
(下りの速さ)=(静水時の速さ)+(流れの速さ)
であることを利用すると下りのときの静水時の速さは、\(4.8-0.2=時速4.6時間\) ということになります。
これは、上りのときの静水時よりも \(5-4.6=0.4\)だけ遅くなっているということがわかりましたね。
答え
時速0.4時間
比を使って考える!
ここでは、速さと時間の逆比を使って考えます。
同じ道のりを進む場合、速さの比と時間の比は逆になるというものでしたね。
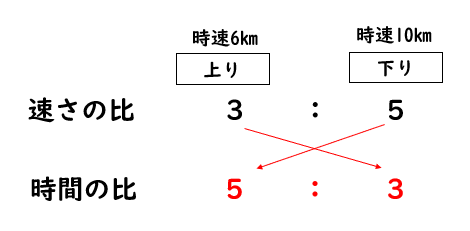
ということは、往復で16時間かかったということから
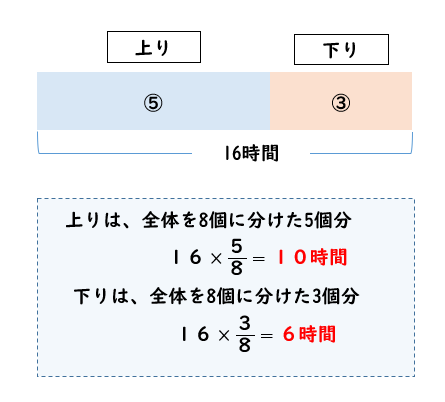
上りの時間は10時間、下りの時間は6時間ということがわかります。
上りと下りのどちらで計算してもよいですが、速さと時間がわかったのでここからある地点の距離を求めることができます。
$$6\times 10=60㎞$$
答え
60㎞
流水算まとめ!
お疲れさまでした!
流水算の問題を解くためには、以下の基本公式をしっかりと頭に入れておきましょう。
下りの速さ
(静水時の速さ)+(川の流れの速さ)
上りの速さ
(静水時の速さ)ー(川の流れの速さ)
川の流れの速さ
(下りの速さ ー 上りの速さ)÷2
その上で、応用問題などでは比を使ったり、旅人算の考えを使ったりします。
さすがに中学受験の問題は難しかったですね(^^;)
だけど、ここはひたすら練習あるのみです。
いろんな問題に挑戦して、知識の幅を広げていきましょう。

















コメントを残す