【入試難問に挑戦！】連立方程式の解が存在しない問題とは！？

今回挑戦する問題はこちら

難関高校の入試に出題された連立方程式に関する問題です。

 

ぜひ、挑戦してみましょう！

連立方程式の解が存在しないとは？

この問題を解く上で、大切なポイントを確認しておきましょう。

連立方程式の解が存在しないとは？

 

ここで１つ思い出しておきたいのは

ともに一次式である連立方程式の解とは、２直線の交点と同じである。

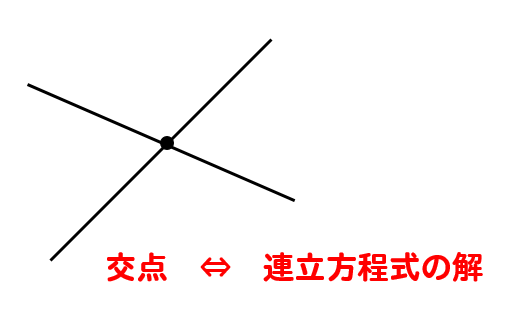
ということです。

 

つまり

連立方程式の解が存在しないとは

『2直線が平行であり、交点を持たない』

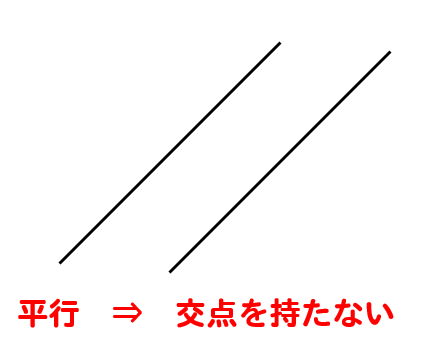
ということになります。

 

 

今回の問題では

2つの方程式を直線として考え

それらが平行になる（傾きが等しくなる）ときを求めれば良いということになります。

問題の解法

それぞれの傾きを求めていきましょう。

まずは、\((-a^2+7a-6)x+2y=4\)

式が複雑なので、慎重に式変形していきましょうね！

$$(-a^2+7a-6)x+2y=4$$

$$2y=-(-a^2+7a-6)x+4$$

$$y=\frac{a^2-7a+6}{2}x+2$$

よって、傾きは

$$\frac{a^2-7a+6}{2}$$

であることがわかります。

 

 

次は、\(ax+y=a\)

こちらはシンプルで簡単ですね！

$$ax+y=a$$

$$y=-ax+a$$

よって、傾きは\(-a\)ということがわかりました。

 

 

それぞれの傾きが等しくなれば平行になるので

$$\frac{a^2-7a+6}{2}=-a$$

この方程式を解いて\(a\)の値を求めます。

$$\frac{a^2-7a+6}{2}\times 2=-a\times 2$$

$$a^2-7a+6=-2a$$

$$a^2-5a+6=0$$

$$(a-3)(a-2)=0$$

$$a=3,2$$

 

 

このように、それぞれの式が平行になるのは

\(a=3,2\)のときであるとわかりました。

 

 

よっしゃ！答え出たぜ！

と、焦ると落とし穴にハマってしまいます…

 

実は、それぞれの式が平行であっても

交点を持ってしまうときがあります。

 

それは…

2つの式が、全く同じものになってしまったときです。

 

 

なので、\(a=3,2\)のときに平行になることはわかりましたが、それぞれの値のときに同じ式になってしまっていないかを確認する必要があります。

 

では、それぞれ確認していきます。

\(a=3\)のとき

\((-a^2+7a-6)x+2y=4\)に代入して式を求めると

$$y=-3x+2$$

\(ax+y=a\)に代入して式を求めると

$$y=-3x+3$$

となり、それぞれの式は別物であることがわかります。

よって、\(a=3\)は答えとしてOKということになります。

 

一方

\(a=2\)のとき

\((-a^2+7a-6)x+2y=4\)に代入して式を求めると

$$y=-2x+2$$

\(ax+y=a\)に代入して式を求めると

$$y=-2x+2$$

となり、それぞれは同じ式になってしまいます。

これでは、交点を持ってしまうので問題の条件を満たさないことになってしまいます。

よって、\(a=2\)は答えとしてNGということになります。

 

 

以上より

今回の問題の答えは

まとめ

お疲れ様でした！

難しい問題ではありましたが、連立方程式や一次関数に関する知識や考え方をしっかりと身につけておくことができれば対応することのできた問題でしたね！

応用力を高めていくためには、こうやってたくさんの問題に挑戦して知識の引き出しを作っていくことが大切です。

 

恐れず、どんどん難しい問題に挑戦していきましょう！