【関数y=ax2乗】放物線グラフの書き方はこれでバッチリ！

今回は中3で学習する『$y$は$x$の二乗に比例する関数』という単元から、$y=ax^2$のグラフの書き方について解説していくよ！

このグラフは、定期テストだけではなく入試にも良く出てきます。

しっかりとマスターしておきたいですね(^^)

今回の記事はこちらの動画でも解説しています(/・ω・)/

Contents

放物線のグラフの特徴
放物線グラフの書き方
分数の場合の書き方
2学期からでも最短で結果を出す！遅れを取り戻して一気に入試レベルまで引き上げる新講座
y＝ax2乗のグラフ書き方　まとめ

放物線のグラフの特徴

$y=ax^2$という形をした関数のグラフは

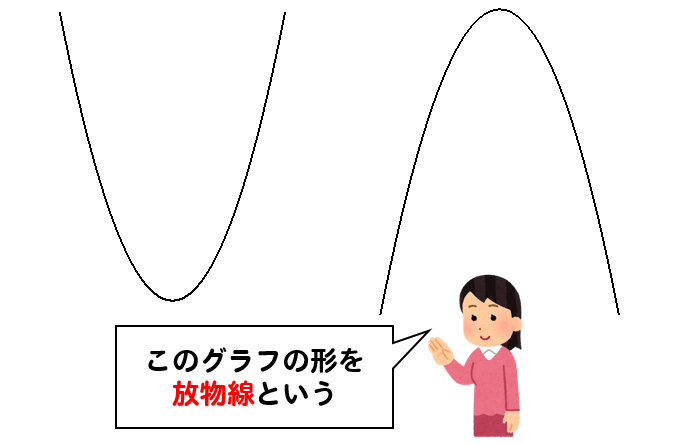
このような放物線と呼ばれるグラフになります。

放物線というワードは定期テストで問われることもあるから覚えておこう！

このワードをテストで出題すると

間違って『放射線』と書いちゃう人がいるんだよね。

採点者のウケを狙っている場合ではないので、しっかりと『放物線』と答えてくださいｗ

そして、この放物線に関連して覚えておきたい用語がいくつかあります。

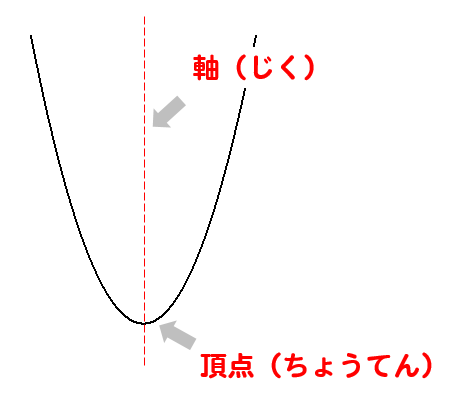
放物線のてっぺんの部分を頂点といいます。

そして、放物線は左右対称になっているのですが

その折れ目となる線のことを軸といいます。

『頂点』『軸』

この2つのワードもおさえておきたいですね。

さらに、放物線には2種類の形があります。

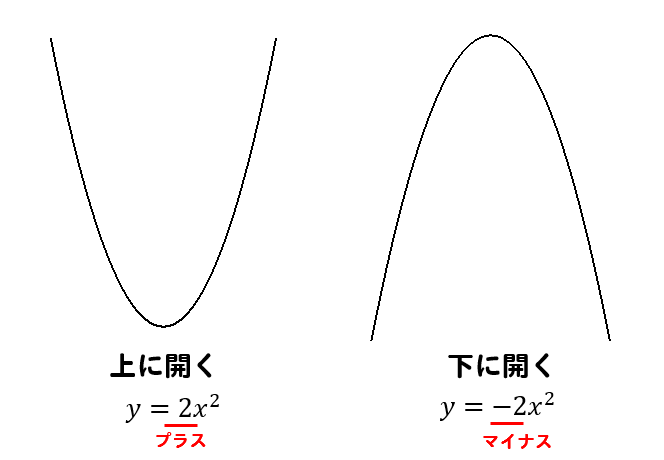
頂点が下にあり、上に広がっていく形の放物線を『上に開く放物線』といいます。

$y=ax^2$の$a$の部分がプラスのときには、この形になります。

一方で、頂点が上にあり、下に広がっていく形の放物線を『下に開く放物線』といいます。

$y=ax^2$の$a$の部分がマイナスのときには、この形になります。

それでは、放物線の特徴や用語を覚えたところでグラフの書き方について詳しく見ていきましょう。

放物線グラフの書き方

例題

次のグラフを書きなさい。

$$\Large{y=x^2}$$

放物線のグラフを書くためには

まず、表を埋めていきましょう！

（表は簡単なやつでいいから自分で作ってね）

それぞれの$x$の値を$y=x^2$に代入すると$y$の値を求めることができます。

値の求め方を詳しく知りたい方はこちら

$x=-3$のとき

$$y=(-3)^2=9$$

$x=-2$のとき

$$y=(-2)^2=4$$

$x=-1$のとき

$$y=(-1)^2=1$$

$x=0$のとき

$$y=0^2=0$$

$x=1$のとき

$$y=1^2=1$$

$x=2$のとき

$$y=2^2=4$$

$x=3$のとき

$$y=3^2=9$$

なんでこんな計算なんだ？という方は文字式の代入について復習しておきましょう。

【中１文字式】計算のやり方を１から丁寧に！

すると、表はこのように埋めることができます。

表が完成したら

ここから座標を読み取っていきます。

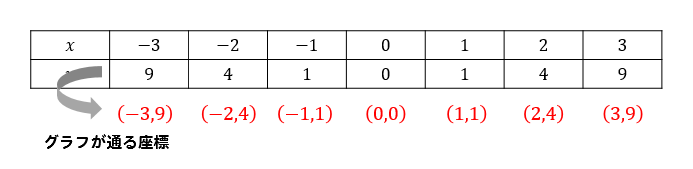
座標が読み取れたら

これらの座標をグラフに書いていきましょう。

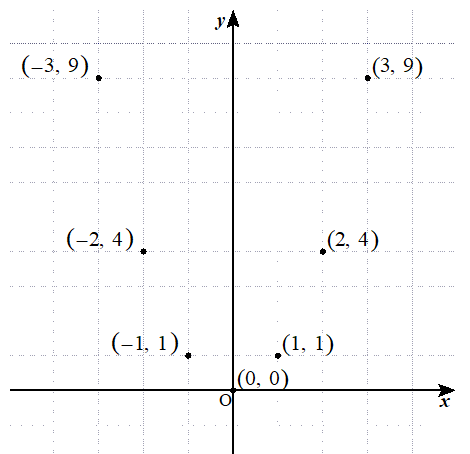
座標が取れたら、あとはこれらの点を滑らかにつなげていくだけです。

ポイントは…

なめらかです！！

定規は使わず、フリーハンドでなめらかーに…

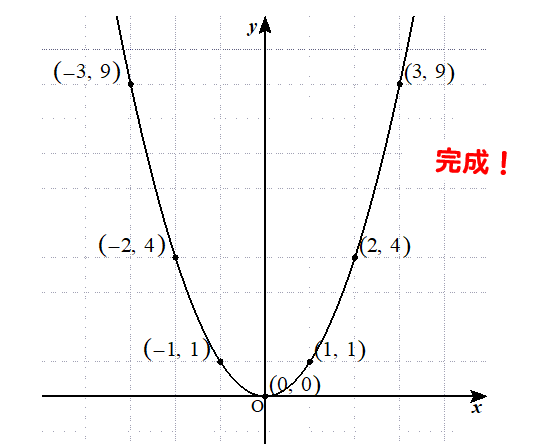
これで完成！！

フリーハンドで書かないといけないから慣れるまでは難しいかもしれませんね(^^;

たくさん練習してキレイな放物線が書けるようにしていきましょう。

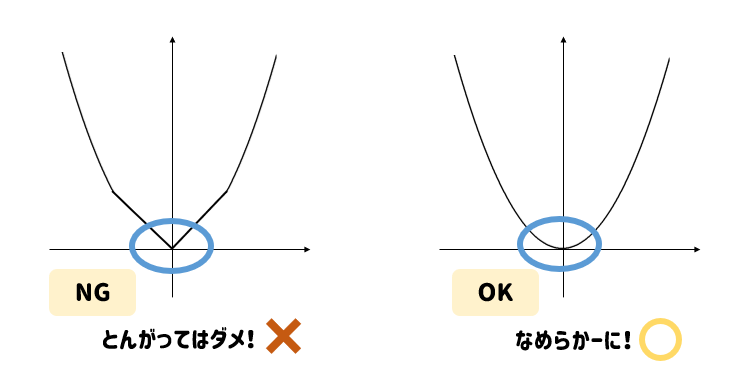
頂点がとんがってしまうとミスになります。

頂点も含めてなめらかな曲線になるよう注意してくださいね！

放物線のグラフを書く手順

表を埋める
座標を読み取ってグラフに書き込む
点をなめらかに結ぶ（頂点もなめらかーに！）

分数の場合の書き方

次に、式に分数が出てくる場合の放物線について解説しておきます。

例題

次のグラフを書きなさい。

$$\Large{y=-\frac{1}{2}x^2}$$

こちらも手順は同じです。

まずは表を埋めていきましょう。

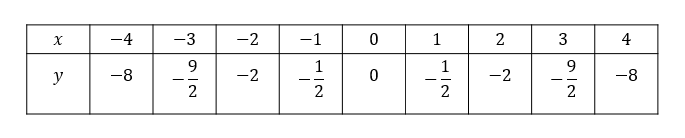
するとね

困ったことに、値が分数になってしまう箇所がでてきちゃうんだよね。

座標を読み取るときに、分数の値があると正確に点がとれないので困ってしまいます。

だから

分数は無視します！

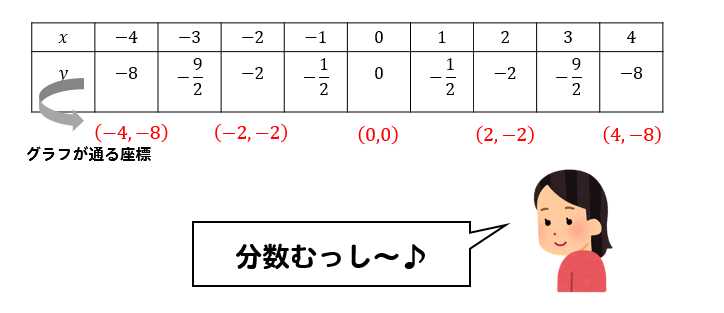
値が分数になってしまう座標は無視して

そうでない値だけ点を取っていきましょう。

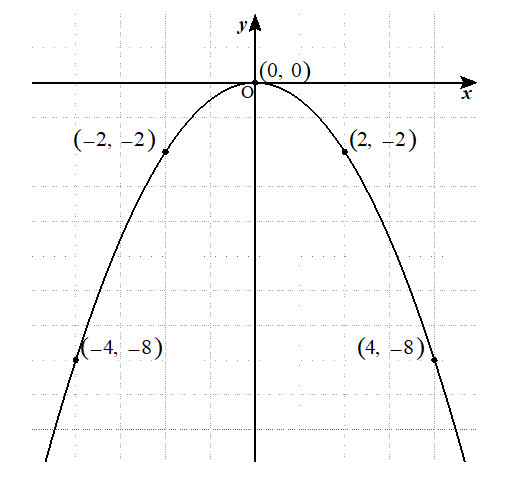
そうすれば、このようにグラフが完成します(^^)

分数がでてきて困ったときには

無視する！

これがポイントですね(^^)

2学期からでも最短で結果を出す！遅れを取り戻して一気に入試レベルまで引き上げる新講座

2学期に入り、入試が目前に迫ってきました。

「模試の点数が下がってしまった…」

「このままで大丈夫なのか…入試への不安が大きくなってきた」

「ウチの子がなかなか本気になってくれない」などなど

受験に対する悩みは尽きないですよね(^^;)

夏休みの施策が上手くいき、成績をガツンと伸ばすことに成功した方はこの調子でがんばっていけばOK！

一方で、現状の成績に不安を感じている、夏の遅れを取り戻したい…と感じている方は、

「入試過去問」×「王道パターン」×「動画」

この3つの要素を組み合わせた学習法を取り入れてみましょう。

そうすることで、ここからでも短期間でも成績を伸ばすことが可能です！

僕が教えてきた生徒さんの中でもこの学習法を取り入れることで、

2学期の時点で偏差値40前半

↓

入試本番で70点をクリア！（おそらく偏差値55くらい）

このような劇的UPを達成しているんですよ＾＾

ニガテな数学でこれだけ点を伸ばすことができれば、すっごく余裕ができますよね！

他にも次のような効果を実感することができます。

ニガテな数学がどんどん解けるようになって、勉強に自信がつく！他教科もがんばれるようになる。

動画を使ってお子さん1人でも学びを完結できる。親は見守っているだけで勝手に成長、点を伸ばしていく！

やったところがテストに出るので、遠回りすることなく最短で点数UPにつながる！次の模試で効果を実感できるかも！

塾に通わせなくても自宅だけで完結！時間、労力、費用を節約しながら効率よく合格をつかみとる！

受験だけでなく、高校進学後にも活きる数学の土台ができあがる！

今回はそんな「入試過去問」×「王道パターン」×「動画」という効率よく点数を伸ばしていく3要素を取り入れた教材を用意しました。

それがこちらです！