今回は、中学3年生で学習する
『\(y\)は\(x\)の2乗に比例する \(y=ax^2\)』
という単元の変化の割合の求め方について解説していきます。
ここでの変化の割合の求め方には
基本形で求める方法の他に
実は、すっごく計算をラクにしてしまう
裏ワザ公式なるものがあります。
学校では教えてもらえない公式だったりするので
ここで学んだことをコッソリと使って
みんなよりも得をしちゃって欲しい。
では
基本形を使った解き方
裏ワザ公式を使った解き方
それぞれ確認していきましょう。
今回の記事はこちらの動画でも解説しています(/・ω・)/
変化の割合の求め方(基本形)とは
まず、押さえておきたいのがこの形

(\(y\)の増加量)÷(\(x\)の増加量)
これを計算してやることで変化の割合を求めることができます。
これが基本的な解き方です。
ただ、公式を文字だけで書かれても非常に分かりにくい!
なので例題を使って解き方を解説していきますね。
例題

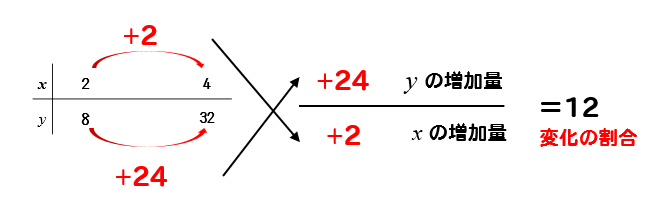
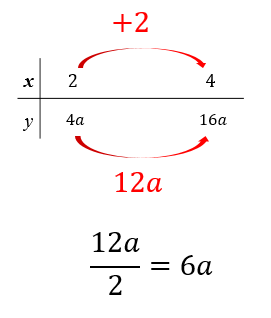
\(x\)と\(y\)がそれぞれどれくらい増加したのかを求めるために
このように表を作ります。

\(x\)の値が2から4まで増加したときの変化の割合を求めたいので表の\(x\)のところには2と4を書いておきます。
\(x\)の値が書けたら、その下に対応する\(y\)の値を求めていきます。
\(x=2\)のとき、\(y=2x^2\)の式に代入してやると
\(y=2\times 4=8\)となり
\(x=4\)のとき
\(y=2\times 16=32\) となるので
表はこのように完成します。

表が完成すれば、それぞれの増加量を見ていきましょう。
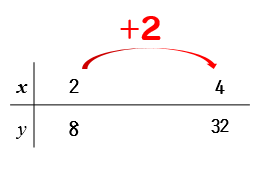
\(x\)の値は2から4に変化しているので
4-2=2 となり
\(x\)の増加量は2
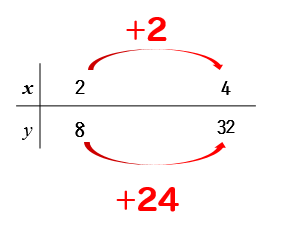
\(y\)の値は8から32に変化しているので
32-8=24 となり
\(y\)の増加量は24
それぞれの増加量が求まれば、基本形の式に当てはめていきます。
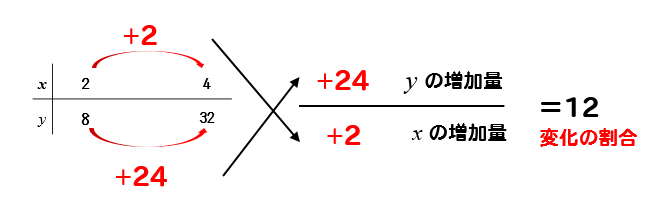
このように変化の割合を求めていきます。
手順としては
- 表を書く
- \(x\)、\(y\)の増加量を求める
- (\(y\)の増加量)÷(\(x\)の増加量)を計算する
これだけです。
どんな式であってもこの手順で解けますよ!
裏ワザ公式とは!?
それでは、次は裏ワザ公式を使って変化の割合を求める方法です。
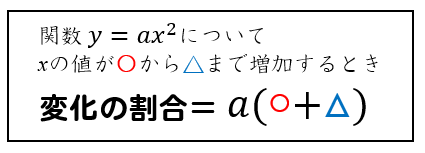
なんと!
この式に当てはめてやれば
面倒な表を書いたり
分数の形にしたりといった
作業を全部すっ飛ばして解くことができます。
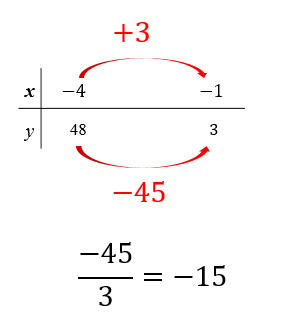
では、先ほどの例題で裏ワザ公式を使ってみましょう。
問題

問題文に印をつけている数字を拾ってきて、裏ワザ公式に当てはめてみます。
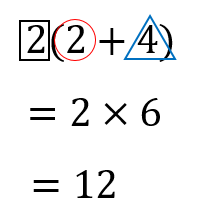
すると、こんなにもあっさりと答えが出てきちゃいました。
裏ワザ、楽すぎるーーーー!!

ん、待てよ。
そもそも何でこんな公式で求めることができるんだ?
納得いかねぇ!
オレは納得いかないモノは使わねぇ主義だ!

という方は、裏ワザ公式が成り立つ理由も書いておくので
納得できたら使ってみてくださいね。
いやいや、公式だけ覚えて答えが出せれば
それでいいや…

って方は次の問題演習に挑戦してみましょう。

問題演習で理解を深めよう!
それでは、変化の割合の解き方を
問題演習を通してマスターしていきましょう!
大体、この4パターンが解ければ大丈夫だと思います。
挑戦してみましょう!
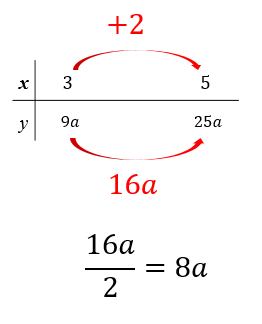
問題①

問題②

問題③

問題④
関数\(y=x^2\)について、\(x\)が\(a\)から\(a+2\)まで増加するときの変化の割合が\(5\)である。このとき、\(a\)の値を求めなさい。
y=ax² 変化の割合の解き方 まとめ
変化の割合の基本的な求め方は

このような形で求めることができました。
それぞれの増加量は表を作って
(変化後の値)ー(変化前の値)
を計算することで求めることができます。
そして
このように表や分数の形を使わなくても
簡単に求めることができる裏ワザ公式がありましたね。


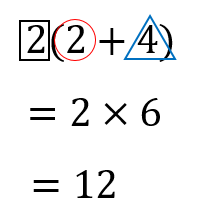
この裏ワザ公式を使いこなせるようになると
応用問題になればなるほど力を発揮してくるので
あなたの得点アップに貢献してくれるはずですよ!
しっかりと練習して身につけていきましょー
ファイトだーーーー!!
変化の割合の裏ワザ公式とは?←今回の記事



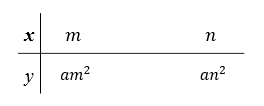
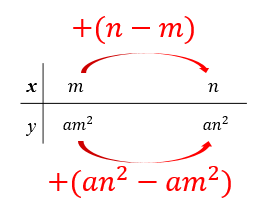
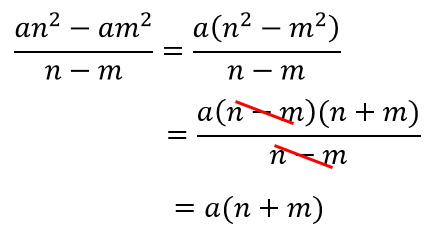
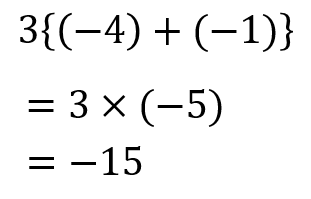
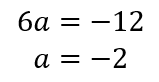
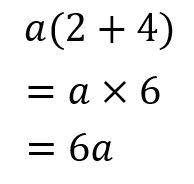

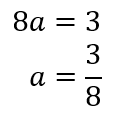













本当に3秒で解けました(^^♪
裏ワザが成り立つ理由も読みました。
こっそり裏ワザ使います。
ありがとうございました。
YouTube登録しました。
毎日見て勉強します!
確かに!
いつもコメントありがとうございます^^
こっそり裏ワザを使って
こっそり友達よりもいい点をとっちゃってください!
YouTube登録もありがとうございます!!
まじでこれのおかげで今まで悩んでいたものが解消できた!
ありがとうございます!
右に同じく_(:3」∠)_
悩みが解消して助かりました!!