【中3数学】y＝ax2乗の変域の求め方を解説！

今回は中3で学習する

『yはxの2乗に比例する　y=ax²』

の単元で、変域の求め方について解説していきます。

• yの変域を求める
• xとyの変域から式を求める

この2つの問題について解説をしていきます。

yの変域を求めるのが基礎

それぞれの変域から式を求めるのが応用

といった感じですね。

応用だけ学びたい人は

目次から応用部分に飛んでいってくださいね(^^)

では、いきましょー！

今回の記事はこちらの動画でも解説しています(/・ω・)/

変域とは？？

そもそも変域って？

変域っていうのは簡単に言い換えると

『範囲』のことです。

xの変域は

ヨコの範囲

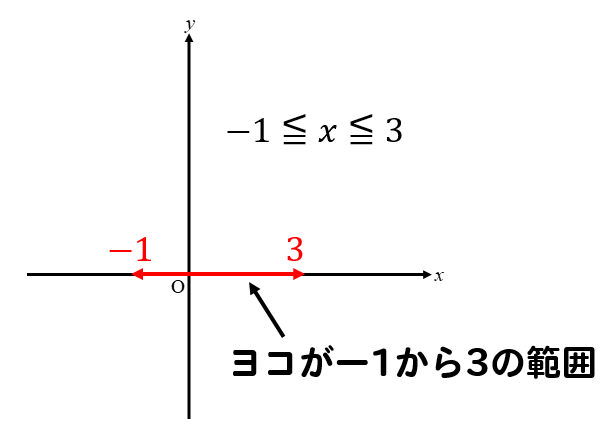
yの変域は

タテの範囲

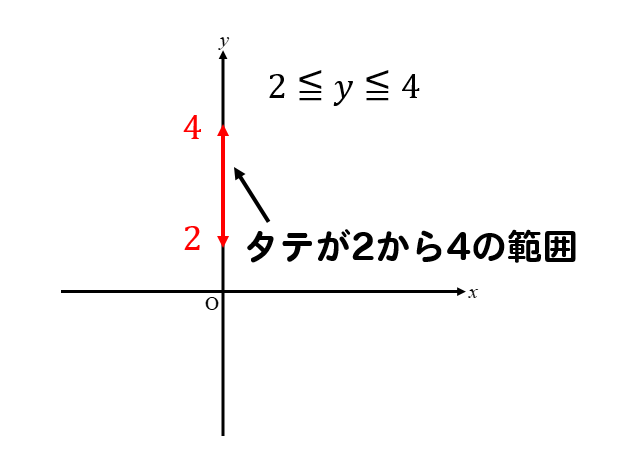
を表していると思ってください。

では、以上のことを頭に入れておいて

問題を見ていきましょう。

yの変域の求め方

変域に関してこのような問題が出題されます。

用語や記号が多くて

何を聞かれているのかが分かりにくいですよね…

それでは

この問題で聞かれていることを

簡単に言い換えてみます。

xの変域が与えられたとき

⇒　グラフをヨコの範囲で切り取ったとき

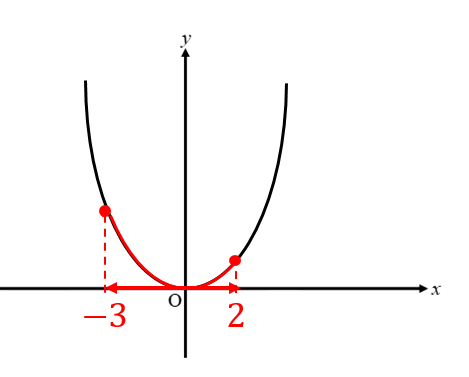
このようにy＝2x²のグラフを

ヨコが－3から2の部分で切り取ります。

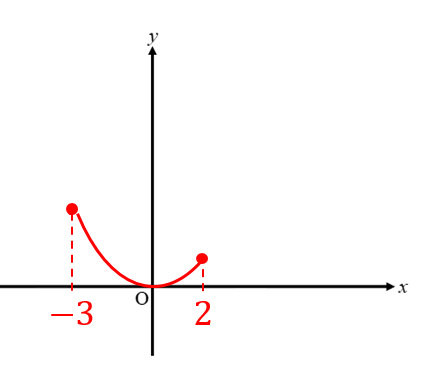
yの変域を求めなさい

⇒　グラフのタテの範囲はどうなる？

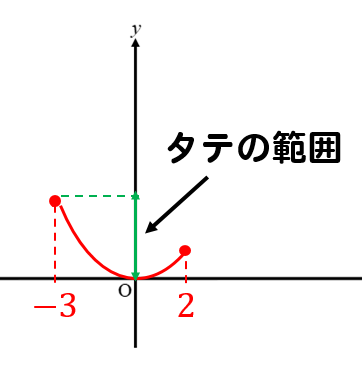
ヨコの範囲で切り取ったグラフを見て

タテの範囲がどうなっているかを見ます。

x＝－3のときの座標は

y＝2x²に代入してやると求めることができますね。

y＝2×(－3)²＝2×9＝18

それを利用してやると、縦の範囲は

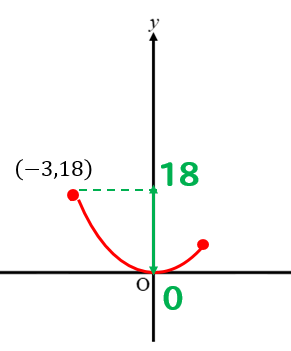
0から18となっています。

よって、yの変域は

0≦y≦18

と書いてやれば答えになります！

つまり、変域の問題とは

『ヨコの範囲でグラフを切り取ると

タテの範囲はどうなりますか？』

というのを記号や用語を使って聞かれているということなのです。

でも

問題を解くときに、毎回グラフを書くの？

めんどーーーーーい…

ごもっとも！笑

というわけで

グラフを書かかずに変域を求める方法も紹介しておきます。

ちょっと楽な変域の求め方

それでは、グラフを書かずに変域を求める方法を

この問題を使って説明していきます。

（1）の変域を求めるには

1≦x≦3の範囲で表を作ります。

表が完成したら、yの数を見て

小≦y≦大と書いてやれば変域を求めることができます。

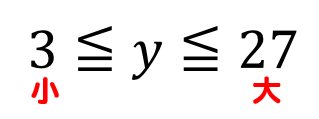
（2）も同じように表を完成させて求めるのですが

ちょっと注意したい点があります。

xの変域の中に0を含む場合には

0の数も表の中に書いてやります。

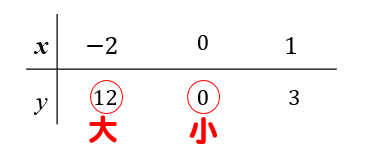
3つ出てきたyの値を見比べて

一番小さい数、大きい数を見つけます。

そして、それらの数を

小≦y≦大と書いてやれば変域を求めることができます。

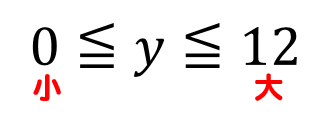
このように

グラフを書かずに表を使って求めるには

• xの変域から表を作る

※xの変域に0を含む場合は0も書いてやりましょう！

• yの値を見比べて、小≦y≦大と並べる

これで変域が完成です！

めっちゃ簡単ですね！

なので、実際に問題を解くときに

グラフを書く必要はありません。

だけど

変域はグラフを切り取って考えている問題なんだな

ってことはちゃんと覚えておいてくださいね！

x、yの変域から式を求める方法

それでは、次は応用編

x、yの変域から式を求める問題の解説をしていきます。

このようにxとyの変域が与えられ

それをヒントに式を求めなさいという問題です。

この問題を解くときのポイントは

グラフの通る座標を見つける！

ことです。

それでは、この問題を解く手順を見ていきましょう。

手順① グラフの形を考える

yの変域を見ると

0≦y≦12

タテの範囲は正となっています。

このことから、放物線のグラフは

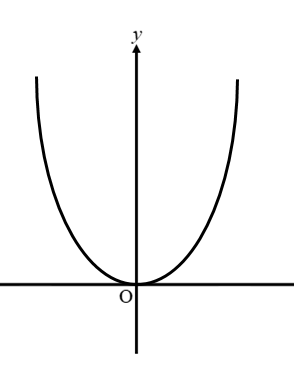
このように上に開いた形になるということがわかります。

yの変域が負になっていれば

グラフは下に開いた形になりますね。

手順② xの変域で切り取る

グラフの形が分かったら

そのグラフをxの変域で切り取ってやります。

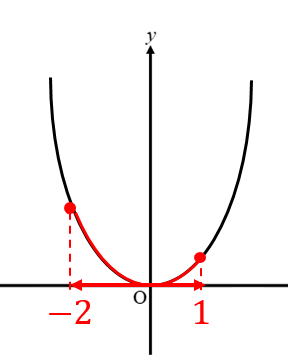
手順③ yの変域を書き込む

xの変域で切り取られたグラフの中に

yの変域を書き込んでいきます。

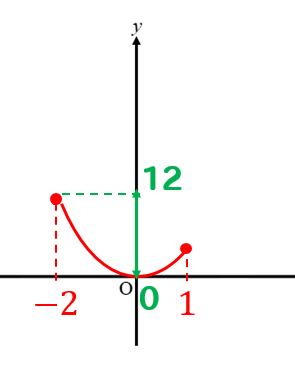
手順④ 座標を見つけて、式を作る

x、yの変域を書き込んでやると

座標が１つ見つかります。

このように見つけた座標を

放物線の式であるy＝ax²の式に代入してやると

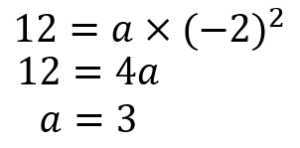
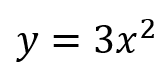
このように式を求めてやることができます。

変域はグラフを切り取ること

っていうイメージが持てている人は

応用問題でもしっかりと対応することができるはずです！

変域の問題 まとめ

yの変域を求める場合は

グラフを書いてヨコの範囲を

切り取りながら考える方法もるけど

表を書いてやれば簡単に求めることができましたね！

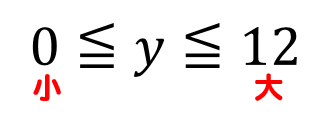
x、yの変域から式を求める場合には

しっかりと手順を踏んでいく必要がありました。

• 手順① グラフの形を考える

• 手順② xの変域で切り取る

• 手順③ yの変域を書き込む

• 座標を見つけて、式を作る

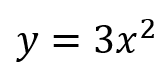
このような手順で式を作ることができます。

あとは、たくさん問題演習をやって

理解を定着させていきましょう。

ファイトだー！！