今回は中3で学習する
『\(y\)は\(x\)の2乗に比例する\(y=ax^2\)』
の利用問題である
平均の速さに関する問題の解説をしていきます。

今回の内容はこちらの動画でも解説しています(/・ω・)/
平均の速さの求め方は?
平均の速さは、変化の割合と同じ方法で求めることができます!
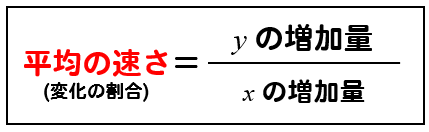
変化の割合の求め方については
こちらで詳しく解説しているので
やり方がわからない方は
確認してみてください(^^)
裏ワザ公式の紹介もありますよ!
それでは、問題解説へ移っていきます。
問題解説!
問題
物を落とすとき、落ち始めてから\(x\)秒後に落ちる距離を\(y\)mとすると、\(y\)は\(x\)の2乗に比例する。
20mの高さから物を落とすとき、地面に着くまでに2秒間かかった。
このとき、次の問いに答えなさい。
(1)\(y\)を\(x\)の式で表しなさい。
(2)落ち始めてから5秒間では、何m落ちるか答えなさい。
(3)180mの高さから物を落とすとき、地面に着くまでに何秒間かかるか求めなさい。
(4)落ち始めてから1秒後から5秒後までの平均の速さを求めなさい。
(1)の解説!
(1)\(y\)を\(x\)の式で表しなさい。
問題文の中に
『\(y\)は\(x\)の2乗に比例する』
とあることから
式は\(y=ax^2\)の形になることがわかります。
普通は問題文を読み解いて
比例かな?反比例かな?
いやいや一次関数かな?
と、どの式を用いていけば良いのかを見極めないといけないのですが
2乗に比例する単元では、問題文の中に
これは2乗に比例しますよ~って書いてくれてることが多いんですよね。
だから
他の関数問題に比べるとすごく易しいです。
次は問題文のここから
『20mの高さから物を落とすとき、地面に着くまでに2秒間かかった』
\(x=2\)のとき、\(y=20\)になる
ということが読み取れれば
\(y=ax^2\)の式に代入してやって
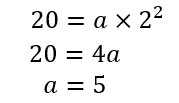
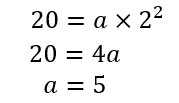
式は
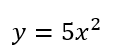
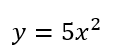
このように求めることができます。
(2)の解説!
(2)落ち始めてから5秒間では、何m落ちるか答えなさい。
これは
\(x=5\)のとき、\(y\)の値は?
と聞かれていることと同じです。
(1)で求めた式に\(x=5\)を代入してやると
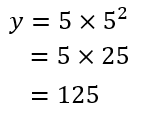
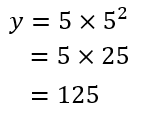
これで、答えは125mとわかりました。
(3)の解説!
(3)180mの高さから物を落とすとき、地面に着くまでに何秒間かかるか求めなさい。
これは
\(y=180\)のとき、\(x\)の値は?
ということなので
(1)で求めた式に、\(y=180\)を代入すると
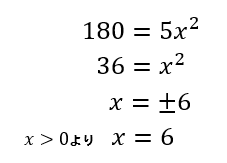
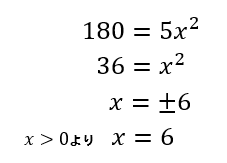
よって、答えは6秒間ですね。
(4)の解説!
(4)落ち始めてから1秒後から5秒後までの平均の速さを求めなさい。
さて、本題ですね!
平均の速さを求めるには
変化の割合と同じ解き方をします。
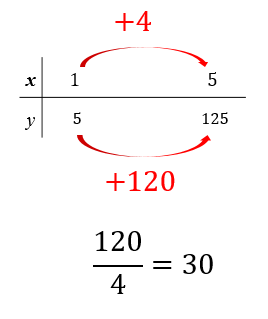
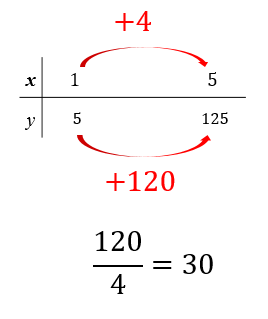
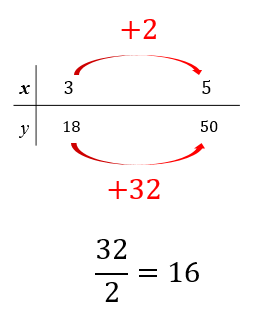
もしも、裏ワザ公式を使って解くなら
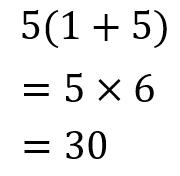
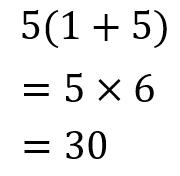
こうですね。
よって、答えは30m/s(秒速30m)となります。
速さを聞かれているので単位をしっかりとつけてくださいね。
変化の割合を求めることができれば
平均の速さの問題はバッチリのはず(^^)


問題演習で理解を深めよう!
問題
ある斜面でボールを転がすとき、ボールが転がり始めてから\(x\)秒間に転がる距離を\(y\)mとすると、\(y=2x^2\)という関係がある。
このとき、次の問いに答えなさい。
(1)動き始めてから3秒間に進む距離を求めなさい。
(2)動き始めてから、3秒後から5秒後までの平均の速さを求めなさい。
(1)動き始めてから3秒間に進む距離を求めなさい。
(2)動き始めてから、3秒後から5秒後までの平均の速さを求めなさい。
関数 平均の速さ まとめ
平均の速さは、変化の割合を計算することで求めることができます。
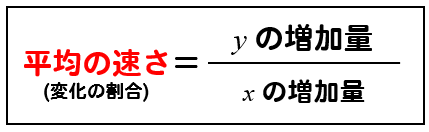
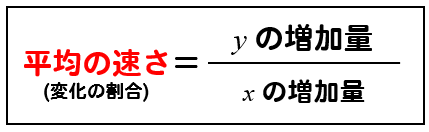
これを覚えておけば大丈夫ですね!
あとは、練習問題を通して理解を深めていってください(^^)
ファイトだー!
利用問題、平均の速さの求め方とは?←今回の記事




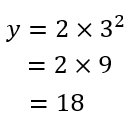
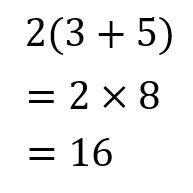













数学は奥が深いなぁ