今回は、指数法則というものを取り上げて解説していくよ！
指数というのは
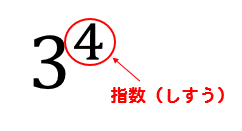
このように、数の右上についている小さい数のことでしたね。
$$2^3\times 2^2$$
$$2^5\div 2^3$$
$$(2^3)^2$$
このように、指数を含む数同士を計算するときに
覚えておきたい特徴があります。
それをまとめて指数法則といいます。
指数法則とは
それでは、指数法則とはどういうものか見ていきましょう。
乗法
$$\large{a^2 \times a^3=a^{2+3}=a^5}$$
掛け算のときには、指数の数を足した値になります。
なぜ、掛け算なのに足し算？って思っちゃいますが
$$a^2\times a^3=(a\times a)\times (a\times a\times a)=a^5$$
2乗と3乗の掛け算では、このように合計で5回掛け算をしているってことになるよね！
だから、乗法では指数の数を足せばOKということになります。
$$3^2\times 3^3=3^{2+3}$$
$$=3^5$$
$$=243$$
$$2x^2y\times 3xy^4=6x^{2+1}y^{1+4}$$
$$=6x^3y^5$$
累乗
$$\large{(a^2)^3=a^{2\times 3}=a^6}$$
$$\large{(ab)^2=a^2b^2}$$
累乗のときは、指数同士を掛けた値になります。
なんで掛け算！？
$$(a^2)^3=a^2\times a^2\times a^2$$
$$=a^{2\times 3}$$
$$=a^6$$
このように\(a^2\)を3乗すると
\(a^2\)を3回掛けるということですよね。
つまり、全部で\(a\)は2×3個ということになります。
$$(ab)^2=(ab)\times (ab)=a^2b^2$$
これも同様に考えればOKですね！
累乗のときには、指数は掛ける！ですね。
$$(-2x^2y^3)^2=4x^{2\times 2}y^{3\times 2}$$
$$=4x^4y^6$$
$$2ab\times (-3a^3b)^3=2ab\times (-27a^9b^3)$$
$$=-54a^{10}b^4$$
除法
$$\large{a^5\div a^2=a^{5-2}=a^3}$$
割り算のときには、指数同士を引いた値となります。
なぜ引き算？
$$a^5\div a^2=\frac{a^5}{a^2}$$
$$=\frac{aaaaa}{aa}$$
ここで分母と分子の\(a\)を2個ずつ約分すると
$$=a^3$$
このように、割り算のときには約分ができちゃうんですね！
だから、それぞれの指数を引いた値となるわけです。
$$3^5\div 3^2=3^{5-2}$$
$$=3^3$$
$$=27$$
$$a^5b^3\div ab^2=a^{5-1}b^{3-2}$$
$$=a^4b$$
乗法なら足し算
累乗なら掛け算
除法なら引き算
というように計算を使い分けていってください。
それでは、指数法則の理解を深めるために計算問題に挑戦してみましょう！
指数法則の計算問題
次の計算をしなさい。
$$2^4\times 2^3$$
次の計算をしなさい。
$$(abc^2)^2\times 2a^2b^3c$$
次の計算をしなさい。
$$(2a^2b)^3\div 2ab^2$$
まとめ
お疲れ様でした！
指数法則について理解は深まりましたでしょうか？
指数法則による計算は
どの単元においても必須となるスキルです。
たくさん演習問題を繰り返して
しっかりと身につけておきましょう！
では、最後に指数法則をまとめて終わりとしましょう。
$$\large{a^m\times a^n=a^{m+n}}$$
$$\large{(a^m)^n=a^{m\times n}}$$
$$\large{(ab)^m=a^mb^m}$$
$$\large{a^m \div a^n=a^{m-n}}$$
とてもわかりやすかったです！
中1娘に教えるのに役立ちました。
ありがとうございました。
お役に立てて良かったです＾＾
数学で困ったことがあれば
他の記事も参考にしてくださいね！