今回は高校数学Ⅱで学習する円の方程式の単元から
『円の中心、半径を求める』
ということについて解説していきます。
取り上げるのは、こんな問題！
次の円の中心の座標と半径を求めよ。
$$x^2+y^2-6x-4y-12=0$$
円の中心、半径の求め方
中心の座標と半径を求めるためには、円の方程式を次の形に変形する必要があります。
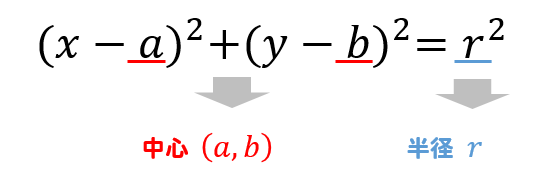
こうすることで、中心と半径を読み取ることができます。
というわけで、円の方程式を変形していきます。
まずは、並べかえて\(x\)と\(y\)をまとめます。
$$x^2-6x+y^2-4y-12=0$$
次に\(x\)と\(y\)について、それぞれ平方完成していきます。
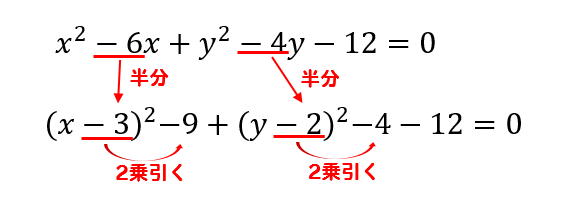
平方完成ができたら、残りモノは右辺に移行しましょう。
$$(x-3)^2+(y-2)^2=25$$
最後に右辺を\(〇^2\)の形に変形すれば
$$(x-3)^2+(y-2)^2=5^2$$
完成！
この式の形から
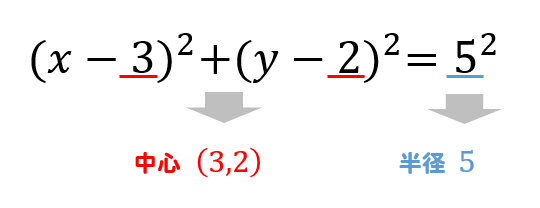
このように中心と半径を読み取ることができました！
円の中心と半径を求めるためには、平方完成して式変形する！
ということでしたね。
手順を覚えてしまえば簡単です(^^)
それでは、解き方の手順を身につけたところでもう1問だけ解説しておきます。
それがこれ！
次の円の中心の座標と半径を求めよ。
$$9x^2+9y^2-54y+56=0$$
なんか\(x^2,y^2\)の前に9がついているぞ…
ややこしそうだ(^^;)
こういう場合には、どのように式変形していけば良いのか紹介しておきます。
\(x, y\)について平方完成をしていくのですが、係数がついているときには括ってやりましょう。
$$9x^2+9(y^2-6y)+56=0$$
$$9x^2+9\{(y-3)^2-9\}+56=0$$
$$9x^2+9(y-3)^2-81+56=0$$
$$9x^2+9(y-3)^2=25$$
ここから、全体を9で割ります。
$$x^2+(y-3)^2=\frac{25}{9}$$
$$x^2+(y-3)^2=\left(\frac{5}{3}\right)^2$$
よって、中心\((0,3)\)、半径\(\displaystyle{\frac{5}{3}}\)となります。
このように、\(x^2,y^2\)の前に数があるときには括りだし、最後に割って消す！
このことをやっていく必要があります。
覚えておきましょう！
それでは、練習問題に挑戦して理解を深めていこう！
円の中心、半径を求める練習問題！
次の円の中心の座標と半径を求めよ。
（1）\(x^2+2x+y^2-3=0\)
（2）\(x^2+y^2-4x-8y+2=0\)
（3）\(4x^2+4y^2-8x+16y-5=0\)
まとめ
お疲れ様でした！
円の中心、半径を求めるためには平方完成ができなければなりません。
二次関数の単元でしっかりとマスターしてもらったかと思いますが、不安が残る方はこちらで練習をしておきましょう！
中学生向けの英文法サイトを開設！
≫ 中学英語の文法まとめサイト！