今回は高校数学Ⅱで学習する円の方程式の単元から
『弦の長さを求める』
について解説していきます。
切り取る線分の長さ（弦の長さ）とは
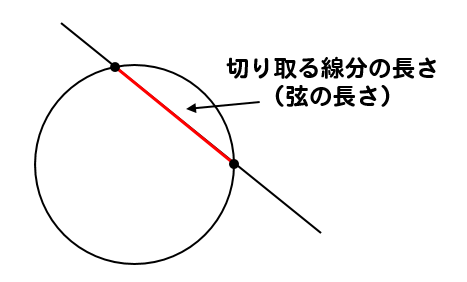
こういった部分のことだね。
それでは、弦の長さを求める手順について解説していくよ！
今回の内容をサクッと理解したい方はこちらの動画がおススメです！
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾
切り取る線分の長さ（弦の長さ）を求める手順
次の問題を取り上げて、弦の長さを求める手順を解説してきます。
円の中心と直線の距離を求める
まずは、準備として円の中心の座標と半径を求めておきましょう。
円の方程式が\(x^2+y^2=16\)であることから
中心の座標は\((0,0)\)、半径は\(4\)であることが読み取れます。
そして、円の中心と直線との距離を求めましょう。
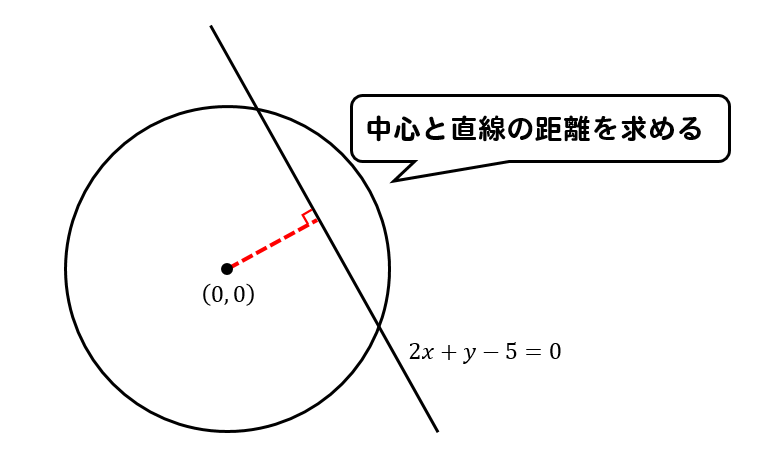
点と直線の距離を求める公式点\((x_1,y_1)\)と直線\(ax+by+c=0\)の距離
$$\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
この公式に当てはめていくと、中心と直線の距離は
$$\frac{|2\cdot 0+1\cdot 0 -5|}{\sqrt{2^2+1^2}}$$
$$=\frac{|-5|}{\sqrt{5}}$$
$$=\frac{5}{\sqrt{5}}$$
$$=\frac{5\sqrt{5}}{5}$$
$$=\sqrt{5}$$
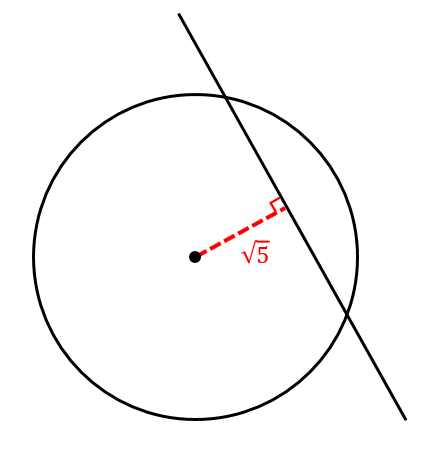
三平方の定理を用いて長さを求める
次に
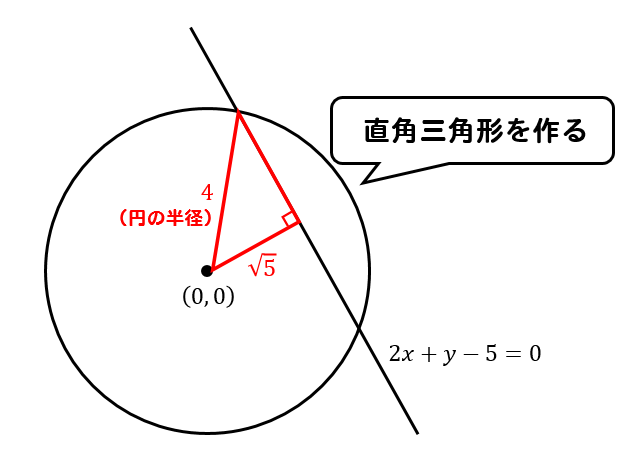
このように線を引いて、直角三角形を作ります。
斜辺は、円の半径にあたる部分だから長さも分かりますね。
そこから、三平方の定理を使って
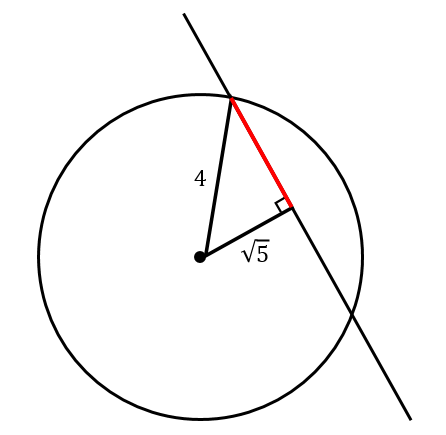
ここの部分の長さを求めます。
求めたい部分の長さを\(x\)とすると
$$4^2=x^2+(\sqrt{5})^2$$
$$16=x^2+5$$
$$x^2=11$$
$$x>0より$$
$$x=\sqrt{11}$$
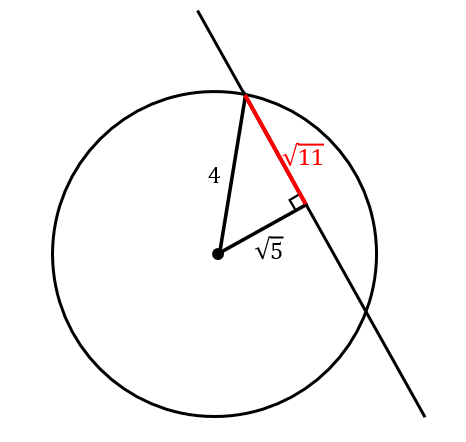
2倍すると完成！
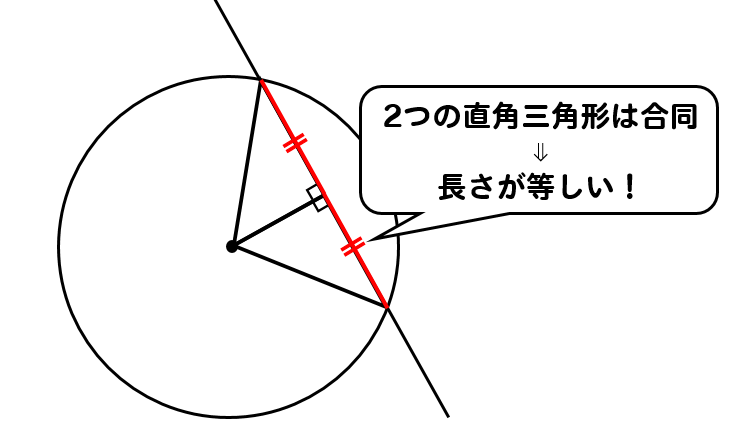
このような関係があるので
先ほど求めた\(\sqrt{11}\)を2倍すると、弦の長さを求めることができます。
よって
$$\sqrt{11}\times 2=2\sqrt{11}$$
完成！
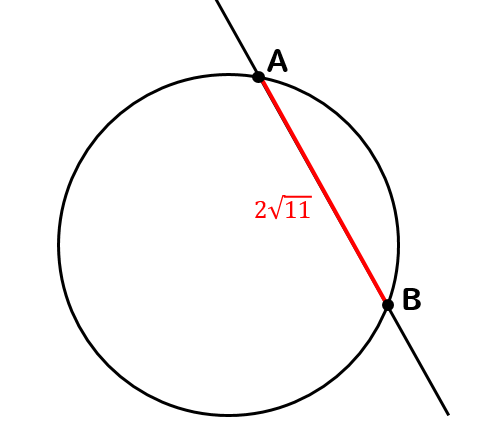
以上の手順で、切り取る線分の長さを求めることができました。
長さを求めるのだから、円と直線の交点座標を求めればよいじゃないか！
そうやって考える人は多いと思います。
しかし…
やってみると断念するはず
交点の座標がめっちゃ複雑になっちゃうからです(^^;)
なので、弦の長さを求める場合には座標を考えるのではなく図形の辺の長さを求めるイメージで考えていってください。
それでは！
理解を深めるために練習問題に挑戦してみましょう。
切り取る線分の長さ（弦の長さ）を求める練習問題に挑戦！
まとめ
お疲れ様でした！
円が直線から切り取る線分の長さ（弦の長さ）を求めるためには
切り取る線分を求める手順
- 中心と直線の距離を求める
- 三平方の定理から長さを求める
- 2倍すると完成！
この３つの手順で求めることができます。
たくさん練習して、しっかりと身につけておきましょう(/・ω・)/
コメントを残す