こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する図形と方程式の単元から「直線の方程式の求め方」についてイチから解説していきます。
取り上げる問題はこちらです!
【問題①】
次の直線の方程式を求めなさい。
(1) 点\((-1,2)\)を通り、傾きが3の直線
(2) 2点\((3,2), (5,6)\) を通る直線
(3) 2点\((2,5), (-3,5)\) を通る直線
(4) 2点\((-2,4), (-2,1)\) を通る直線
【問題②】
点\((3,-2)\)を通り、次の直線に平行な直線、垂直な直線をそれぞれ求めなさい。
(1) \(y=3x-2\)
(2) \(4x-3y+2=0\)
今回の内容をサクッと理解したい方はこちらの動画もおススメです(‘ω’)ノ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
傾きと通る点から求めるパターン
【問題①】
次の直線の方程式を求めなさい。
(1) 点\((-1,2)\)を通り、傾きが\(3\)の直線
直線の式といえば、中学数学ではこのように求めましたね。

ですが、高校生になると後に学習する内容を考慮して、次の式を使って求めていくようになります。
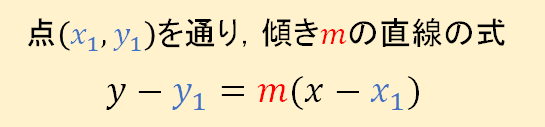
これを使うことによって、中学のときに比べて途中式など減ってラクに求めれます^^
では、実際に使ってみるとこんな感じ!

慣れたら簡単ですよ^^
ってことで、こちらの練習をやっておけば式の形を覚えておきましょう!
【練習問題】次の直線の方程式を求めなさい。
(1) 点\((3,4)\)を通り、傾きが\(-2\)の直線
(2) 点\((1,-2)\)を通り、傾きが\(4\)の直線
2点を通るパターン
【問題①】
次の直線の方程式を求めなさい。
(2) 2点\((3,2), (5,6)\) を通る直線
(1)の問題と違って傾きが与えられていません。
ならば、2点の座標から傾きを求めてやろうじゃないか!ということで、このような式を活用していきましょう。

それぞれの\(x\)座標、\(y\)座標の差を分数にすれば傾きが表せますよね^^
というわけで、次のように求めていきましょう!

傾きを求める部分は慣れるまでは練習が必要かなって感じなので、こちらをどうぞ!
【練習問題】次の直線の方程式を求めなさい。
(1) 2点\((-4,3), (6,-3)\) を通る直線
(2) 2点\((3,-4), (-1,0)\) を通る直線
x、y座標が同じになっているパターン
【問題①】
次の直線の方程式を求めなさい。
(3) 2点\((2,5), (-3,5)\) を通る直線
(4) 2点\((-2,4), (-2,1)\) を通る直線
(2)で取り上げたパターンと同じでは?と思ってしまいますが、与えられた2点をよーく見てください。
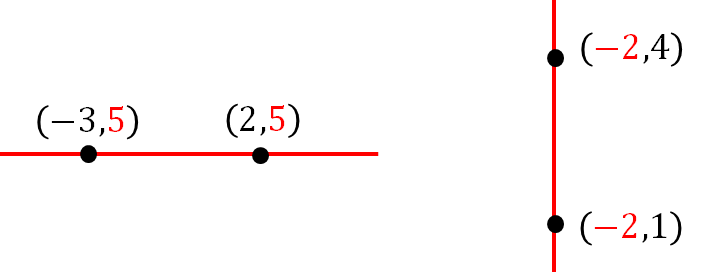
すると、このように\(x\)座標、\(y\)座標が同じになっているので、(2)のように斜めの直線ではなく、縦、横の直線になってしまいますね。
こういった場合には直線の公式とかは無視して、そのまま次のように式を作ってください。


このパターンは計算不要で式がつくれるので、すごくラッキーですよね!
2点の座標が与えられたときには、まず\(x、y\)座標が同じになっているかどうかをチェックするようにしてくださいね。
【練習問題】次の直線の方程式を求めなさい。
(1) 2点\((5,1), (5,10)\) を通る直線
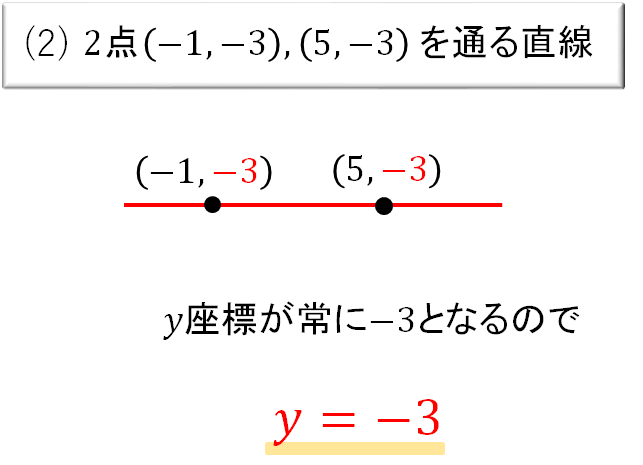
(2) 2点\((-1,-3), (5,-3)\) を通る直線
平行になるパターン
【問題②】
点\((3,-2)\)を通り、次の直線に平行な直線を求めなさい。
(1) \(y=3x-2\)
(2) \(4x-3y+2=0\)
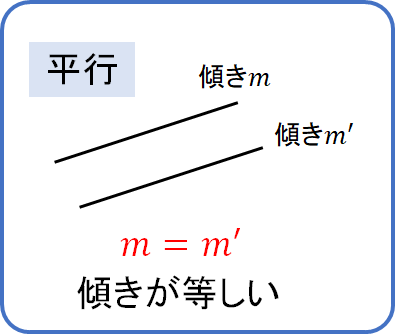
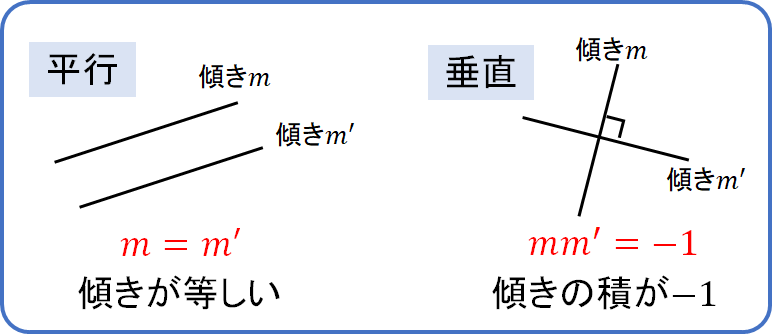
平行な直線 ⇔ 傾きが等しい
これは必ず覚えておきましょう!
なので、今回の問題のポイントは(1)(2)で与えられている直線から傾きを読み取とること。

そうすれば、傾きが与えられているパターンの式にあてはめて解いていくことができますね!


(2)は分母を払って、\(4x-3y-18=0\) としてもOKです!
【練習問題】
点\((3,-1)\)を通り、直線\(3x+2y+1=0\)に平行な直線の方程式を求めなさい。
垂直になるパターン
【問題②】
点\((3,-2)\)を通り、次の直線に垂直な直線をそれぞれ求めなさい。
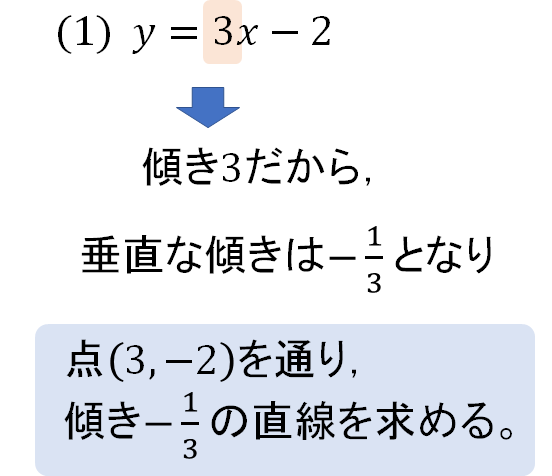
(1) \(y=3x-2\)
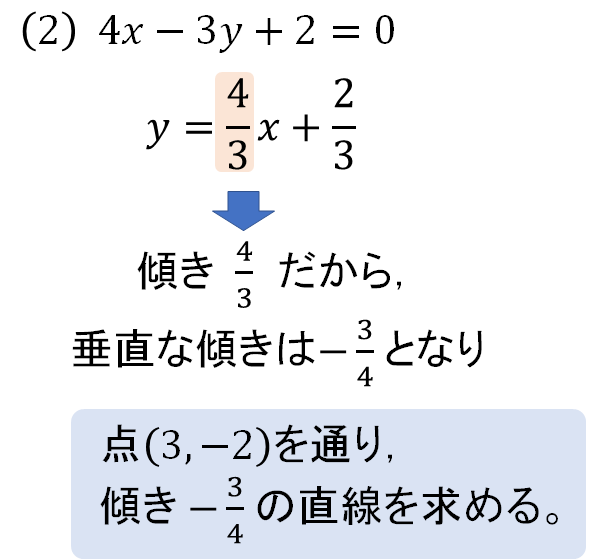
(2) \(4x-3y+2=0\)
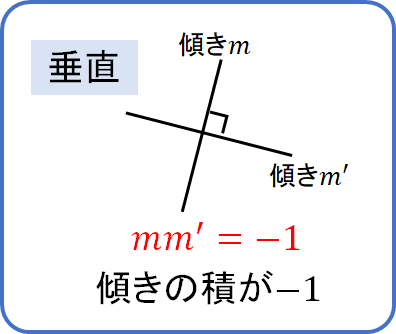
垂直な直線 ⇔ 傾きの積が\(-1\)になる
この特徴を使いながら式をつくっていきますが、垂直な傾きは次のように覚えておくと便利です!

すると、今回の問題は次のように考えることができます。


【練習問題】
点\((3,-1)\)を通り、直線\(3x+2y+1=0\)に垂直な直線の方程式を求めなさい。
まとめ
それではポイントをまとめておきましょう!


以上!
直線の方程式は今後いろんな場面で活用するので、しっかりと身につけておいてくださいね!


























コメントを残す