今回は数学Ⅱで学習する円と方程式の単元から
\(x\)軸、\(y\)軸に接する円の方程式について解説していくよ！
考えていく問題はこちら
\((2,1)\)を通り、\(x\)軸、\(y\)軸に接する円の方程式を求めよ。
x軸、y軸に接する円とは
円が\(x\)軸、\(y\)軸に接するとは次のような状況です。
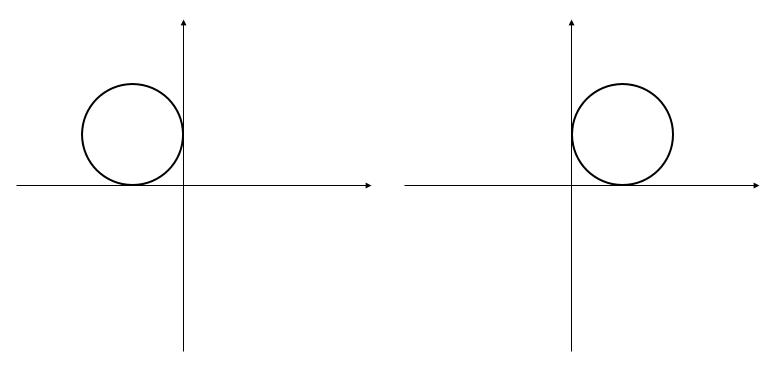
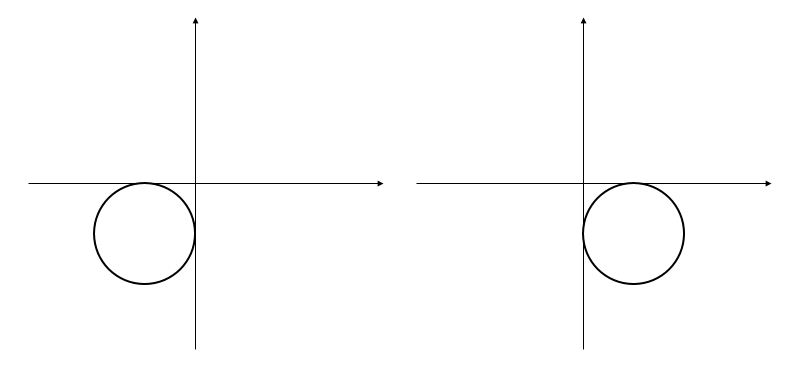
このように４つのパターンが考えられます。
問題で与えられた情報から、上のどのパターンになるかを考える必要があります。
また、すべてに共通していることは
中心の座標の絶対値が同じになる！
ということです。
絶対値というと難しく聞こえるのですが、図で確認すると以下の通りです。
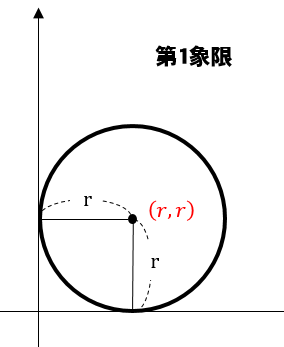
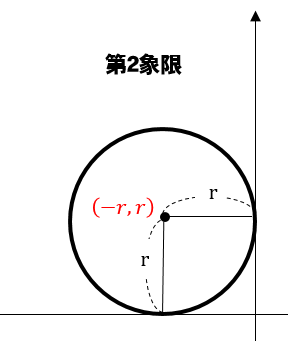
このように、円がどの部分であるのかが判明すれば半径を用いて中心の座標を表してやることができます。
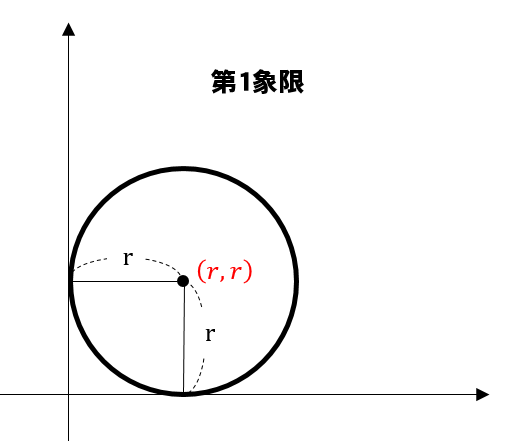
円が第１象限にある場合
中心の座標は\((r,r)\)
円が第２象限にある場合
中心の座標は\((-r,r)\)
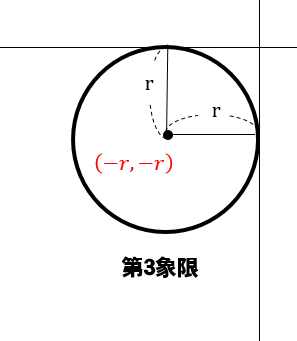
円が第3象限にある場合
中心の座標は\((-r,-r)\)
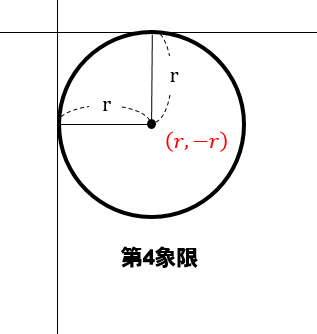
円が第4象限にある場合
中心の座標は\((r,-r)\)
問題の解答＆解説！
今回の問題では、\((2,1)\)を通るということから
第１象限のパターンだということが分かります。
つまり、半径を\(r\)とした場合
求めたい円の中心は\((r,r)\)と表すことができます。
半径が\(r\)であり、中心は\((r,r)\)ということから
求めたい円の方程式は
$$(x-r)^2+(y-r)^2=r^2$$
と表すことができます。
そして、円は\((2,1)\)を通るということから、上の方程式に代入してやります。
$$(2-r)^2+(1-r)^2=r^2$$
すると、このように\(r\)に関する方程式ができるので、これを解いていきましょう。
$$4-4r+r^2+1-2r+r^2=r^2$$
$$r^2-6r+5=0$$
$$(r-5)(r-1)=0$$
$$r=1,5$$
よって、\(r\)の値が2つ求まりました。
なんで2つも？と思っちゃいますが
第１象限、\((2,1)\)を通るという情報だけでは
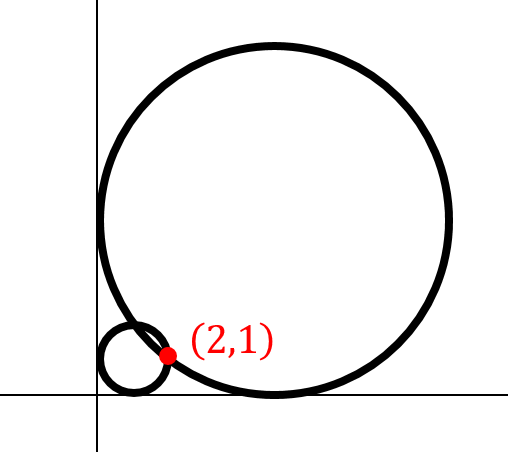
このように2パターンの円が考えられるからですね(^^)
よって、円の方程式は
$$(x-1)^2+(y-1)^2=1$$
$$(x-5)^2+(y-5)^2=25$$
となります。
まとめ
お疲れ様でした！
円が\(x\)軸、\(y\)軸に接する問題では
- 円がどこにできるのか
- 中心はどうやって表せばいいのか
この2点がポイントとなってきます。
今回やったような解き方をしっかりと覚えておきましょう(^^)
円が\(x\)軸、\(y\)軸に接する問題の解き方
- 与えられた座標から円の場所を考える
- 円の中心を半径を用いて表す
- 円の方程式を作り、与えられた座標を代入
- \(r\)の値を求める
- 円の方程式を完成させる！
数学の成績が落ちてきた…と焦っていませんか？
数スタのメルマガ講座（中学生）では、以下の内容を無料でお届けします！
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
コメントを残す