今回は、関数と平行四辺形の融合問題について解説していきます。
- 平行四辺形の頂点の座標を求める方法とは
- 対角線の交点を求める方法とは
- 平行四辺形の面積を二等分する方法とは
- 実践問題に挑戦!
この4本立てでお話を進めていきます(^^)
平行四辺形の頂点の座標を求める
下のような四角形OABCが平行四辺形であるとき
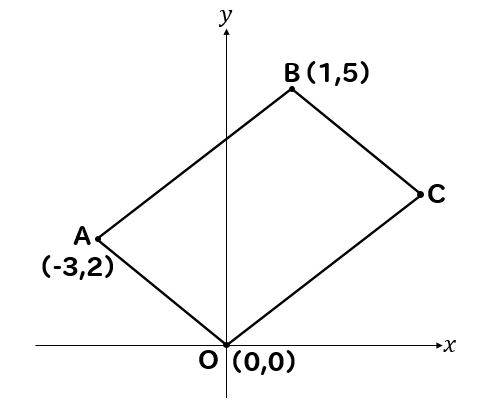
頂点Cの座標を求めるためにはどうすれば良いのか解説していきます。
平行四辺形の特徴である
2組の向かい合う辺がそれぞれ平行である
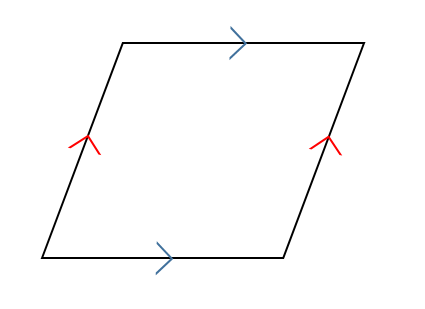
2組の向かい合う辺がそれぞれ等しい
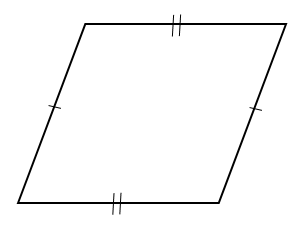
この2つの性質を利用して考えていきます。
すると
$$OA//CB, OA=CB$$
$$AB//OC, AB=OC$$
ということがわかります。
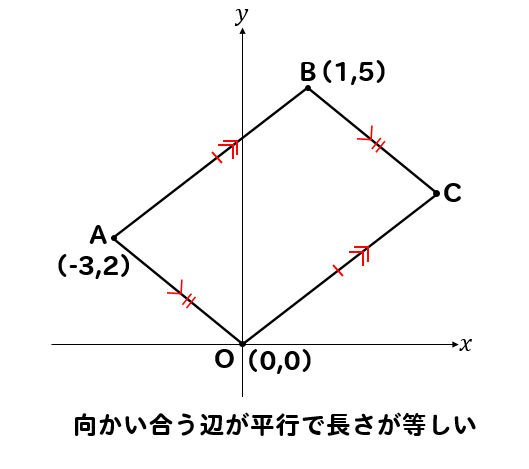
グラフ上で、それぞれの辺が平行で長さが等しいということは

このように、それぞれの移動距離が等しくなるということを表しています。
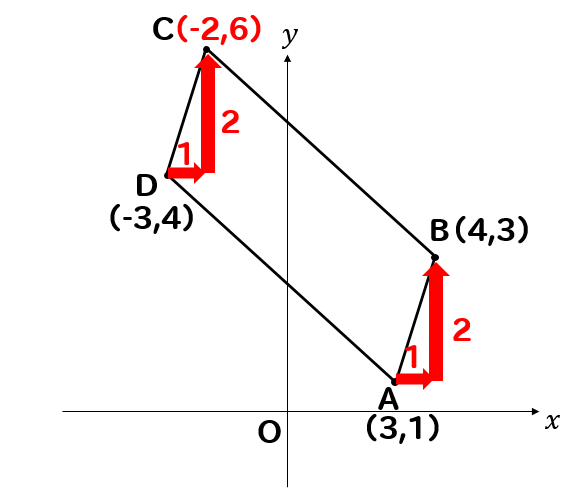
AからOまでは、横に3と下に2移動しているので
同様にBからCまでも横に3と下に2移動しているということになります。
よって、点Cの座標は
点Bを基準にして\(x\)座標は\(1+3=4\)、\(y\)座標は\(5-2=3\)
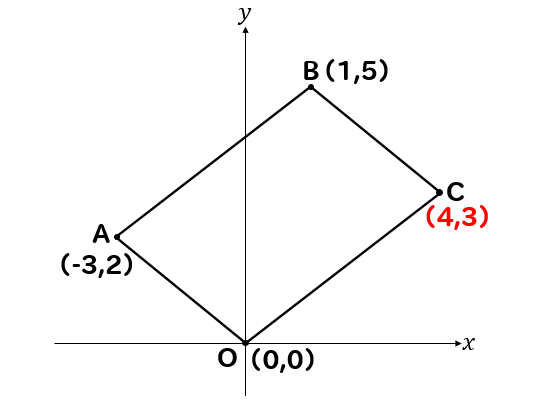
\( C(4,3) \)となります。
平行四辺形の座標を求めたいときには
向かい合う辺が平行で長さが等しくなるという性質を利用して
それぞれの移動距離を調べていけばOKですね(^^)
座標のポイントそれぞれの座標がどれだけ移動しているかを考える!
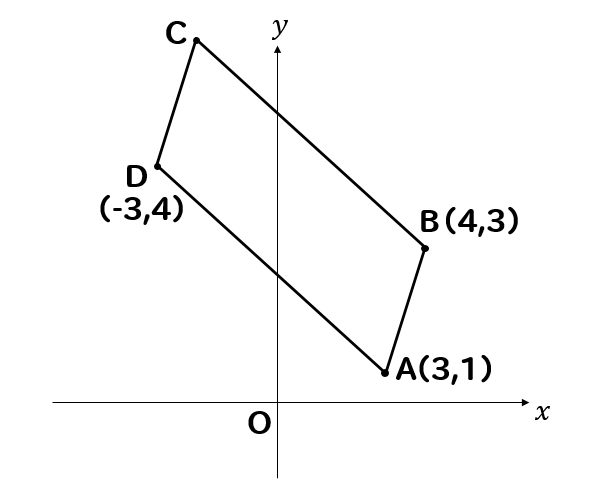
理解を深めておきたい方は練習問題に挑戦してみてください。
次の四角形ABCDが平行四辺形であるとき、点Cの座標を求めなさい。
対角線の交点の座標を求める
平行四辺形の対角線は、それぞれの中点で交わる
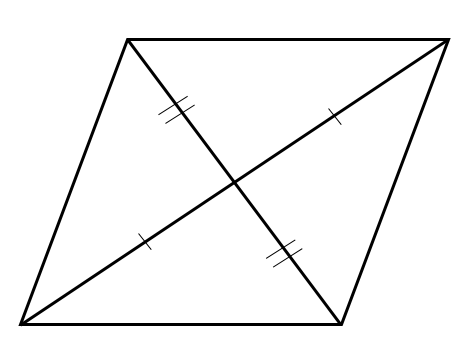
という性質がありましたね。
これを利用して
グラフ上において、それぞれの対角線が交わる点の座標を求めてみましょう。
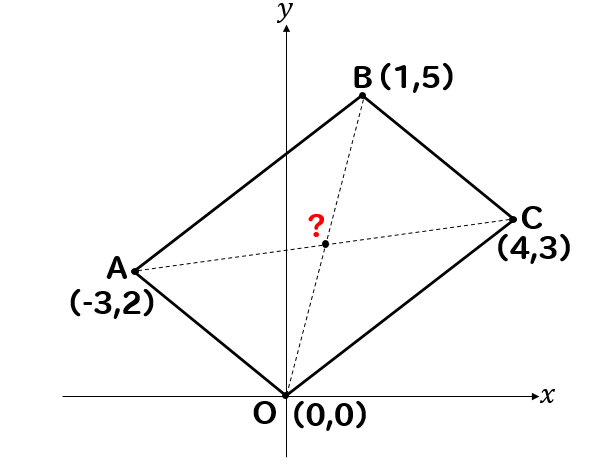
対角線はそれぞれの中点で交わるという性質から
交点の座標は
点AとCの中点、もしくは点OとBの中点に位置しているということになります。

中点の求め方は
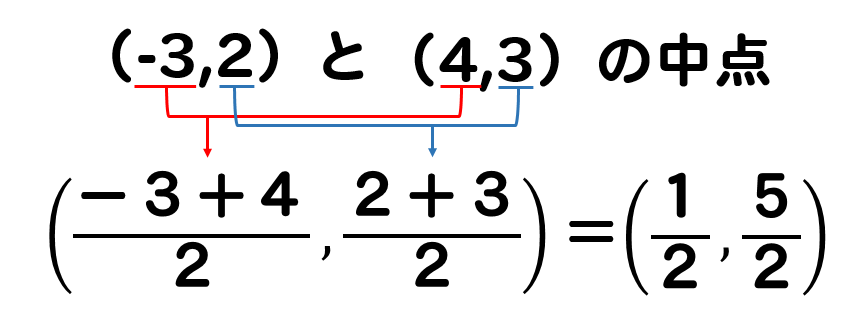
それぞれ足して、2で割る。
これだけでしたね!
よって、対角線の交点の座標は\(\displaystyle \left( \frac{1}{2},\frac{5}{2} \right) \)となります。
問題の解説上、点AとCの座標を利用しましたが
もちろん点OとBの座標を使っても良いからね!
というか、数の小さい座標を利用した方が計算が楽なので
なるべく楽ができるように座標を選んでください(^^)

平行四辺形を二等分する直線
平行四辺形を二等分するような直線の式を考えなさい。
というような問題がよく出題されます。
この問題を解くためには、ちょっとした特徴を知っておく必要があります。
それが…
対角線が交わる点を通るように直線をひくと、平行四辺形を二等分できる!
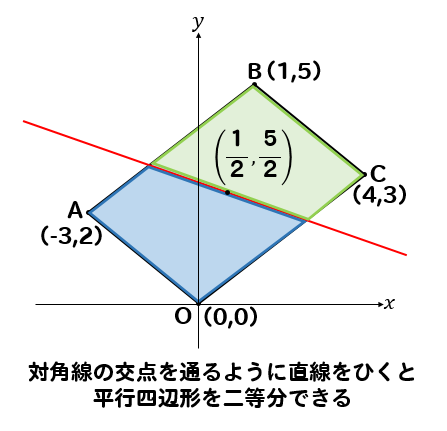
対角線の交点を通るような直線であれば

どんな直線であっても、平行四辺形を二等分することができます。
直線によって、2つに分けられた四角形は
交点を対称の点とする点対称な図形になっているよね。
そこから2つの四角形は面積が等しくなっているってことも分かるはずです。
この性質を知っておけば
平行四辺形の二等分問題は簡単に解けるからね。
ちゃんと覚えておこう!
平行四辺形の二等分対角線の交点を通る直線は、平行四辺形を二等分する
それでは、以上のことを踏まえて
関数と平行四辺形の融合問題に挑戦してみましょう。
放物線と平行四辺形の融合問題を解説!
問題
下の図のように、放物線\(\displaystyle y=\frac{1}{2}x^2\)上に3点A、B、Cがあり、ABは\(x\)軸に平行で、点Aの\(x\)座標は\(-2\)である。\(y\)軸上に点Dをとり、四角形ABCDが平行四辺形になるようにする。このとき、次の問いに答えなさい。
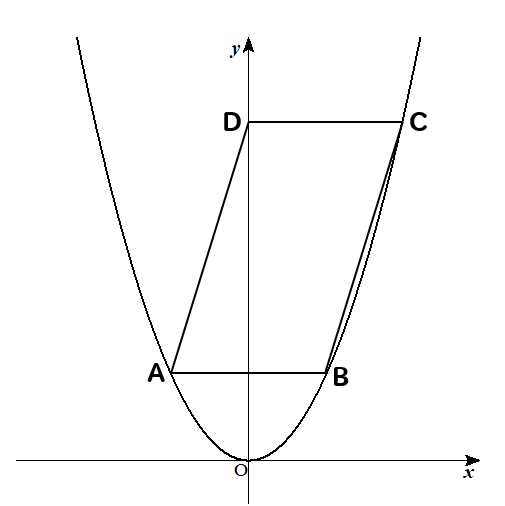
(1)点Bの座標を求めなさい。
(2)点Cの座標を求めなさい。
(3)直線ADの式を求めなさい。
(4)原点Oを通り、平行四辺形ABCDの面積を2等分する直線の式を求めなさい。
(1)放物線は線対称!
まずは、点Aの座標を求めます。
\(x\)座標が\(-2\)ということから
\(\displaystyle y=\frac{1}{2}x^2\)に代入してやると
$$y=\frac{1}{2}\times (-2)^2$$
$$y=\frac{1}{2}\times 4$$
$$y=2$$
よって、点Aの座標は\((-2,2)\)とわかります。
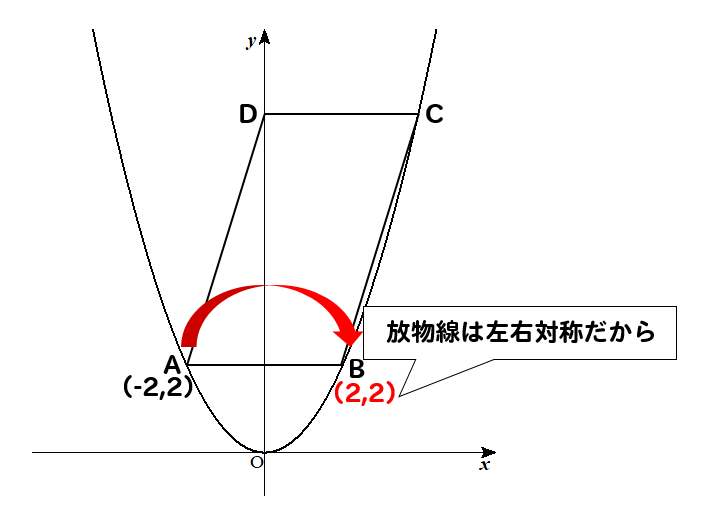
放物線は、\(y\)軸に対して対称になっているので
点Aの座標がわかれば、点Bは簡単ですね!
答え
B(2,2)
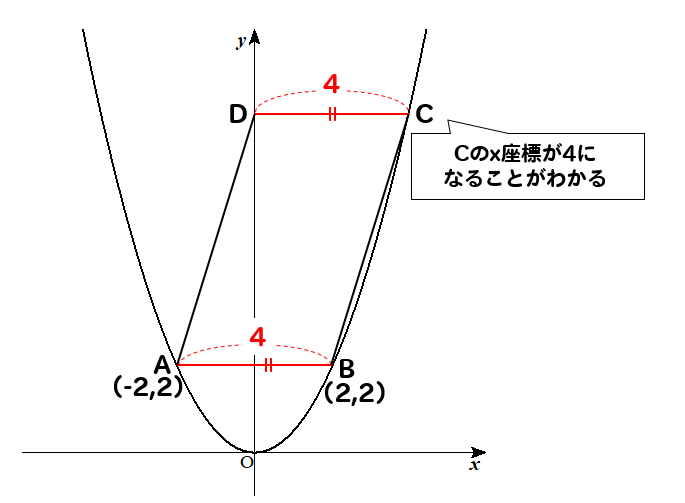
(2)長さが等しいから!
ABの長さが4になるということから
点Cの\(x\)座標が4になるということがわかります。
先ほどと同様
\(\displaystyle y=\frac{1}{2}x^2\)に代入してやると
$$y=\frac{1}{2}\times 4^2$$
$$y=\frac{1}{2}\times 16$$
$$y=8$$
よって、\(C(4,8)\)となります。
答え
C(4,8)
(3)一次関数と平行四辺形
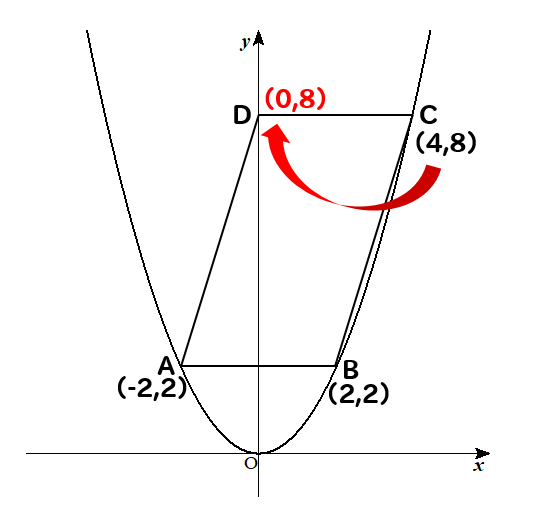
点Dの座標を求めたら
2点\((-2,2),(0,8)\)を通る直線の式を求めていきます。
一次関数の式の作り方を忘れてしまった人は、こちらも参考にしてみてくださいね。
\(y=ax+b\)にそれぞれの座標を代入して
$$2=-2a+b$$
$$8=b$$
これらを解いていくと
$$a=3, b=8$$
よって、直線ADの式は\(y=3x+8\)となります。
答え
$$y=3x+8$$
(4)対角線の中点に注目!
平行四辺形を二等分するためには
対角線の交点を通るように直線をひけば良かったですね。
ということで
まずは、平行四辺形の対角線の交点の座標を求めます。
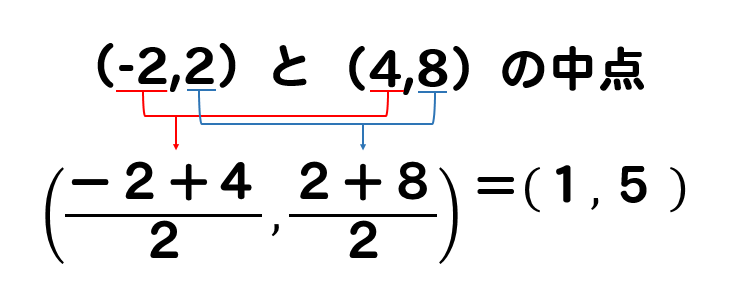
交点の座標が求まったら
2点\((0,0),(1,5)\)を通る直線の式を求めていきます。
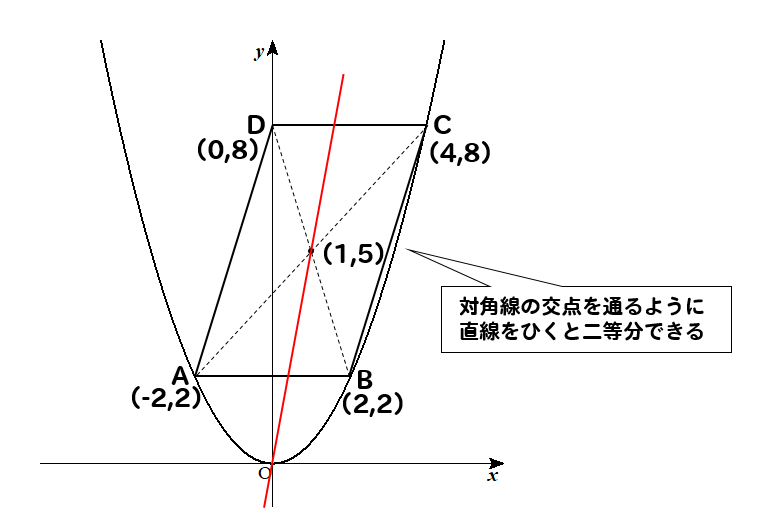
原点を通る直線なので
このグラフは、比例になります。
よって、\(y=ax\)の式を利用して計算していきます。
\((1,5)\)を代入してやると
$$5=a \times 1$$
$$a=5$$
よって、直線の式は\(y=5x\)となります。
答え
$$y=5x$$
まとめ
お疲れ様でした!
関数と平行四辺形の融合問題は、ちょっと応用力が必要になりますね。
だけど、入試問題に出題されることも多いので
今回の記事を通して、理解を深めてもらえればと思います(^^)
また、平行四辺形は向かい合う辺が平行になっているので
平行⇒傾きが等しい
といった特徴を利用することもあります。
直線の式を求めるような問題では、座標が分からない場合
傾きを利用して式を求めることもあります。
これに関する良い問題が見つかれば、こちらの記事で随時更新していきますね!
以上!
ちょっと難しい問題だったけど
しっかりと復習して身につけておこう。
ファイトだー(/・ω・)/

















一次関数の、平行四辺形の面積の求め方も教えていただきたいです。