今回は中2で学習する
『一次関数』の単元から
直線の式の求め方について解説していくよ!
ここでは、いろんなパターンの問題が出題されるので
パターン別に例題を使って解説していきます。
傾き、切片が与えられる
(1)傾きが5で、切片が-2である直線
傾きが与えられる
(2)点(4,5)を通り、傾きが3である直線
変化の割合が与えられる
(3)変化の割合が5でx=2のときy=4である一次関数
切片が与えられる
(4)点(2,5)を通り、切片が3である直線
通る2点が与えられる①
(5)x=-4のときy=1、x=-2のときy=4である一次関数
通る2点が与えられる②
(6)2点(2,8)、(4,4)を通る直線
グラフが平行になる
(7)点(-2,10)を通り、直線\(y=-2x+3\)に平行である直線
グラフが\(y\)軸上で交わる
(8)点(3,-1)を通り、直線\(y=x+5\)とy軸上で交わる直線
対応表が与えられる
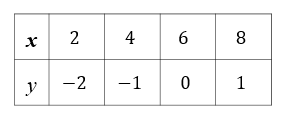
(9)対応するx、yの値が下の表のようになる一次関数
増加、減少の値が与えられる
(10)\(x\)の値が2増加すると、\(y\)の値は6減少し、そのグラフが点(4,-10)を通る一次関数
グラフからの式の作り方については、こちらで紹介してるので参考にしてね!
では、解説いくぞー!!
今回の内容はこちらの動画でも解説してます(‘◇’)ゞ


【一次関数 式の求め方】傾き、切片が与えられる
傾きと切片が分かっている場合には
一次関数の式にそれぞれ当てはめてやれば完成です。


傾き5をaの部分に、切片-2をbの部分に当てはめてやると
答えは\(y=5x-2\)となります。
(1)答え
$$y=5x-2$$
【一次関数 式の求め方】傾きが与えられる
この問題では、傾きは与えられていますが切片が分かりません。
一旦、与えられている傾きだけを式に当てはめてやります。
$$y=3x+b$$
次は、点(4,5)を通るということから
式の中に\(x=4, y=5\)を代入します。
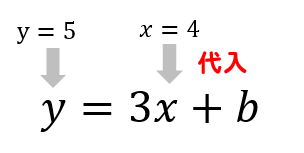
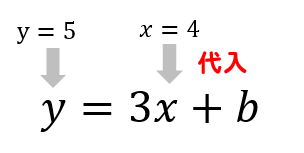
$$5=3\times4+b$$
あとは方程式を解いて、b(切片)の値を求めます。
$$5=12+b$$
$$12+b=5$$
$$b=5-12$$
$$b=-7$$
これで切片が-7だと求まりました。
傾きが3、切片が-7ということより
式は\(y=3x-7\)となります。
傾きだけ与えられている場合には
一旦、式に傾きをあてはめてやり
そこへ通る点の値を代入してやれば
切片を求めることができます。
(2)答え
$$y=3x-7$$
【一次関数 式の求め方】変化の割合が与えられる
ここでのポイントは
一次関数において
変化の割合=傾き
ということです。
つまり、変化の割合が5というのは傾きが5と同じことになります。
そうなれば(2)の問題と解き方は一緒ですね。
変化の割合5をaの部分に当てはめて
$$y=5x+b$$
この式に\(x=2, y=4\)を代入します。
$$4=5\times2+b$$
$$4=10+b$$
$$10+b=4$$
$$b=4-10$$
$$b=-6$$
これで傾き5、切片-6ということは求まったので
式は\(y=5x-6\)となります。
変化の割合が与えられたら、傾きが分かる!
これがポイントですね(^^)
(3)答え
$$y=5x-6$$
【一次関数 式の求め方】切片が与えられている
(2)とは逆で切片が与えられているけど、傾きが分からないというパターンの問題です。
与えられている情報が逆ではありますが、手順は一緒です。
一旦、切片だけを式に当てはめてやります。
$$y=ax+3$$
この式に\(x=2, y=5\)を代入してやります。
$$5=a\times2+3$$
$$5=2a+3$$
あとは方程式を解いてaの値を求めてやります。
$$2a+3=5$$
$$2a=5-3$$
$$2a=2$$
$$a=1$$
これで傾き1、切片3ということが分かったので
式に当てはめてやると\(y=x+3\)となります。
切片が与えられている場合も
一旦は、切片だけを式に当てはめてやり
その式に通る点の値を代入してやると傾きを求めることができます。
(4)答え
$$y=x+3$$
傾きが1だから\(y=1x+3\)としてしまいがちだけど
文字のルールにしたがって、1は省略しようね!


【一次関数 式の求め方】通る2点が与えられる①
今度は、傾きも切片も教えてくれない問題です。


いじわるですね…
こういう場合には
通る点の値を式に代入して2本の式を作ります。


その2本の式から、連立方程式を作って
方程式を解いてやればa(傾き)の値とb(切片)の値を求めてやることができます。
$$\begin{eqnarray} \left\{ \begin{array}{l} 1=-4a+b \\4=-2a+b \end{array} \right. \end{eqnarray}$$
この連立方程式を加減法で解いていきます。
bのところが揃っているので、引き算をするだけでOKですね。
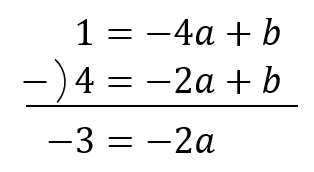
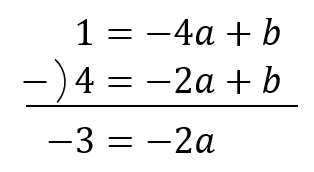
$$-2a=-3$$
$$a=\frac{3}{2}$$
\(1=-4a+b\)に\(a=\frac{3}{2}\)を代入すると
$$1=-4\times\frac{3}{2}+b$$
$$1=-6+b$$
$$-6+b=1$$
$$b=1+6$$
$$b=7$$
以上より、ちょっと計算が長いですが…
傾きが\(\frac{3}{2}\)、切片が7ということが分かりました。
よって、式は\(y=\frac{3}{2}x+7\)となります。
傾きも切片も与えられない場合には
通る2点の値を式に代入して、2本の式から連立方程式を解いてやります。
(5)答え
$$y=\frac{3}{2}x+7$$
【一次関数 式の求め方】通る2点が与えられる②
これは問題の表記が若干違うだけで(5)と全く同じ問題です。
(2,8)を通るというのは
\(x=2\)のとき\(y=8\)になる
と同じことです。
同様に(4,4)を通るというのは
\(x=4\)のとき\(y=4\)になるのと同じですね。
と、いうわけで
式を2本作って、連立方程式を解いていきましょう!
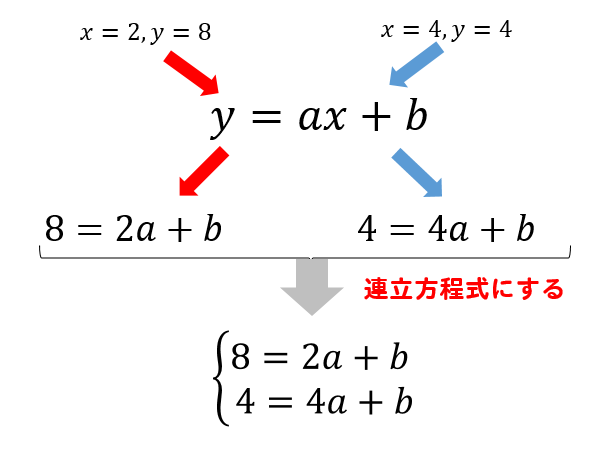

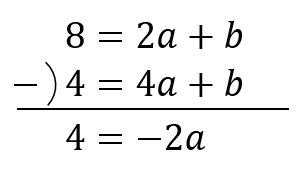
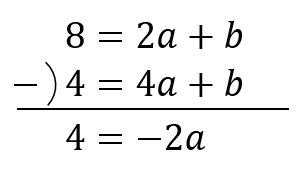
$$-2a=4$$
$$a=-2$$
\(8=2a+b\)に\(a=-2\)を代入してやると
$$8=2\times(-2)+b$$
$$8=-4+b$$
$$-4+b=8$$
$$b=8+4$$
$$b=12$$
よって、傾きが-2、切片が12となり
式は\(y=-2x+12\)となります。
(6)答え
$$y=-2x+12$$
【一次関数 式の求め方】グラフが平行になる
2直線が平行になるというのは
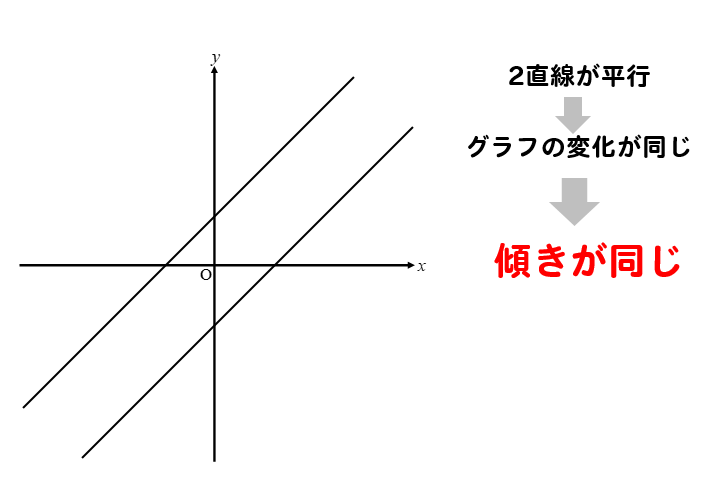

2直線の傾きが等しくなるということです。
つまり
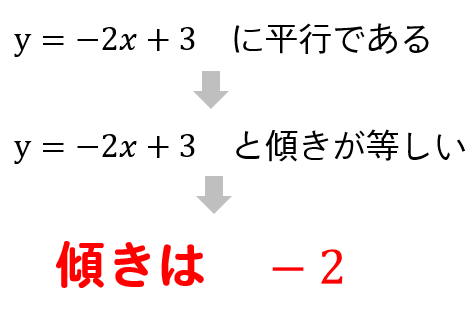

『\(y=-2x+3\)に平行』というヒントから傾きが-2になるということが読み取れます。
そうすると、この問題は
点(-2,10)を通り、傾きが-2である直線の式を求めなさい。と同じことです。
パターンで言えば、(2)と同じですね。
傾きを式に当てはめて計算していくと
$$y=-2x+b$$
\(x=-2, y=10\)を代入して
$$10=-2\times(-2)+b$$
$$10=4+b$$
$$4+b=10$$
$$b=10-4$$
$$b=6$$
よって、傾きは-2、切片は6ということで
式は\(y=-2x+6\)となります。
平行 ⇒ 傾きが等しい
覚えておきましょう!
(7)答え
$$y=-2x+6$$
【一次関数 式の求め方】y軸上で交わるグラフ
\(y\)軸上で交わるというのは、どういう状況かというと


2直線の切片が同じになる!
ということを表しています。
つまり
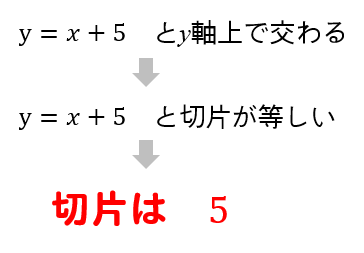

『\(y=x+5\)と\(y\)軸上で交わる』というヒントから切片が5になるということが読み取れます。
そうすると、この問題は
点(3,-1)を通り、切片が5である直線の式を求めなさい。と同じことです。
パターンで言えば、(4)と同じですね。
切片5を式に当てはめて計算していくと
$$y=ax+5$$
\(x=3, y=-1\)を代入して
$$-1=a\times3+5$$
$$-1=3a+5$$
$$3a+5=-1$$
$$3a=-1-5$$
$$3a=-6$$
$$a=-2$$
これで傾きが-2、切片が5とわかるので
式は\(y=-2x+5\)となります。
\(y\)軸上で交わる
⇒ 切片が等しい
覚えておきましょう!
(8)答え
$$y=-2x+5$$
【一次関数 式の求め方】対応表が与えられる
(9)対応する\(x、y\)の値が下の表のようになる一次関数


与えられた対応表から情報を読み取る必要があります。
一番単純なやり方は
対応表から通る2点を読み取ることです。
どこでもいいので、上下の数を見て
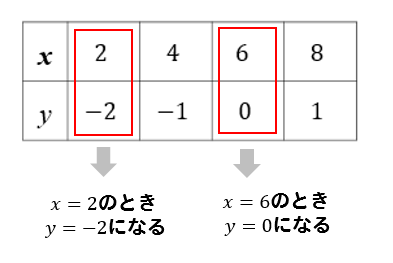

このように情報を読み取っていきます。
(小さい数のとこを選ぶと、計算がラクになるよ)
すると、対応表から
『\(x=2\)のとき \(y=-2、x=6\)のとき\(y=0\)である一次関数』だということが読み取れました。
ここまで来れば(5)(6)と同じパターンだな、と気づけますね!
ということで
2本の式を作って連立方程式で計算していきます。
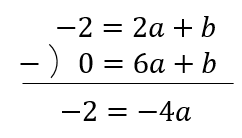
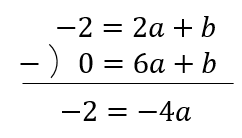
$$-4a=-2$$
$$a=\frac{1}{2}$$
\(0=6a+b\)に\(a=\frac{1}{2}\)を代入してやると
$$0=6\times\frac{1}{2}+b$$
$$0=3+b$$
$$b=-3$$
以上より
傾きが\(\frac{1}{2}\)、切片が-3とわかるので
式は\(y=\frac{1}{2}x-3\)となります。
対応表が与えられたら
通る2点を読み取りましょう!
(9)答え
$$y=\frac{1}{2}x-3$$
【一次関数 式の求め方】増加、減少の値が与えられる問題の解説!
一見、難しそうですが
とってもシンプルな問題です。
『\(x\)の値が2増加すると、\(y\)の値は6減少』
ここの部分をグラフでイメージしてみると
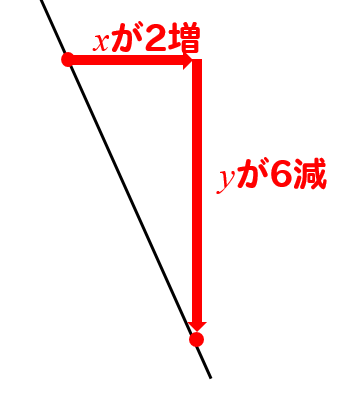

2進んだら、6下がるグラフだということが読み取れます。
よって、傾きは\(-\frac{6}{2}=-3\)ということがわかります。
つまり、今回の問題は
傾きが-3で、そのグラフが点(4,-10)を通る一次関数
と変換することができます。
それでは、傾き-3を式にあてはめて計算していきましょう。
$$y=-3x+b$$
\(x=4, y=-10\)を代入してやると
$$-10=-3\times4+b$$
$$-10=-12+b$$
$$-12+b=-10$$
$$b=-10+12$$
$$b=2$$
以上より
傾きが-3、切片が2とわかったので
式は\(y=-3x+2\)となります。
(10)答え
$$y=-3x+2$$
【特典】これでテストは完璧だ!動画付きの追加演習
さて、ここまでのところで10パターンの式のつくり方はバッチリですか!?
バッチリですよね…(‘◇’)ゞ
ならば、この問題もスラスラ解けますよね!?
ドンッ!!
【追加演習】次の直線の式を求めなさい。
(1)傾き\(3\), 切片\(-2\)
(2)点\((1,-3)\) を通り、傾き\(2\)
(3)変化の割合が\(\frac{2}{3}\)で、\(x=3\) のとき \(y=-1\)
(4)点\((3,5)\)を通り、切片\(7\)
(5)\(x=-2\) のとき \(y=1\)、\(x=4\)のとき \(y=3\)である
(6)2点\((1,2)(4,-7)\) を通る
(7)直線 \(y=-\frac{2}{3}x+5\) に平行で、点\((-6,2)\) を通る
(8)点\((4,2)\)を通り、直線\(y=x+1\)と\(y\)軸上で交わる
(9)対応する\(x,y\)の値が下の表のようになる


(10)\(x\)の値が3増加すると、\(y\)の値は1増加し、そのグラフが点\((-3,-2)\)を通る
これまでに解説してきた問題の数を変えたものを用意しました。
何も見ないでこれらがスラスラと解けるようになっていればしっかりと理解できているという証拠です(‘ω’)ノ
今回の理解を深めるためにもぜひ取り組んでみてくださいね!
追加演習やってみたよ~!!
という方には、こちらから詳しい解説をお渡ししています。
間違えたところもしっかりと見直せるように動画解説も用意しているので、ぜひご活用くださいね!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
答えが合っているかどうかだけでなく、動画解説を活用して『立式のポイント』『情報の読み取り方』といったところもチェックしておいてくださいね^^
解答を受け取ってくれた方には、引き続きいろんな問題をメールでお届けする予定なのでお楽しみに^^
まとめ
お疲れ様でした!
一次関数の式の作り方というのは
定期テストや入試にも必須の問題です。
必ずおさえておきたい問題ではありますが
上で紹介した10パターンをおさえておけば
ほぼほぼ解けるはずです!
いろんな問題に挑戦してみ
解き方が分からなくて困ったときには
このページを参考にしてもらえればなーと思います。
さぁ、いろんな問題集を使って
問題演習だっ!
ファイト―(/・ω・)/
一次関数の式の作り方をパターン別に解説!←今回の記事
一次関数の座標の求め方は?いろんな座標を求める問題について解説!

















ためになった
むずかしい