今回は中2で学習する一次関数の単元からちょっと発展的な
「正方形になる座標」
について取り上げます。
一次関数の応用をマスターしたい方にぴったりの問題となっているので、まずは例題をチェックして演習問題にチャレンジしていきましょう(‘ω’)ノ
今回の問題はこちらの動画でも解説しています。
動画の方が伝わりやすい部分もあるので、サクッと学習したい方はこちらがおすすめです＾＾
【例題】正方形になる座標を求める3ステップ！
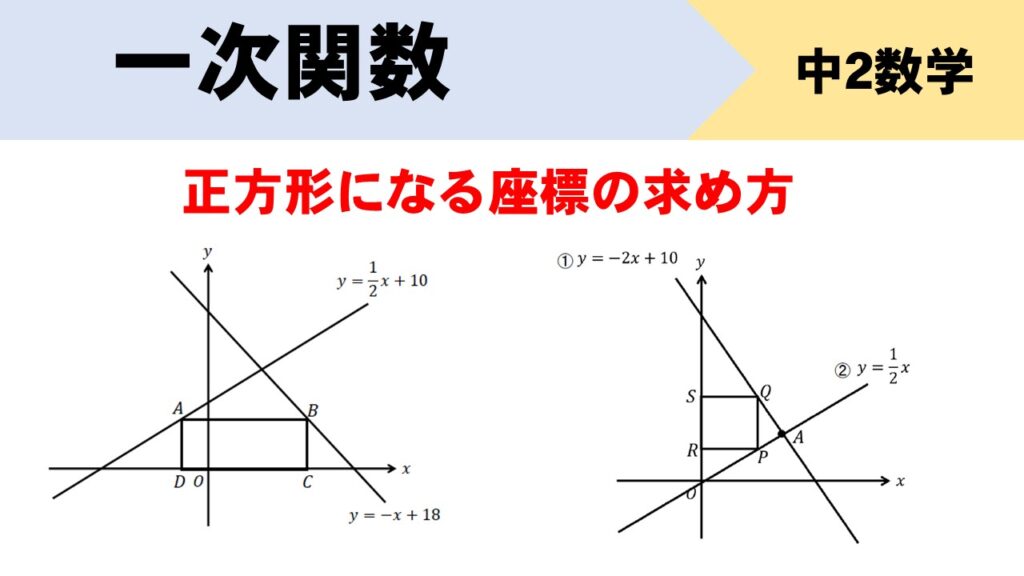
2つの直線上に点A、Bが\(x\)軸と平行になるようにとり、A、Bから\(x\)軸に垂線を下ろして、図のような長方形ABCDをつくる。このとき、長方形ABCDが正方形となるときのAの座標を求めなさい。
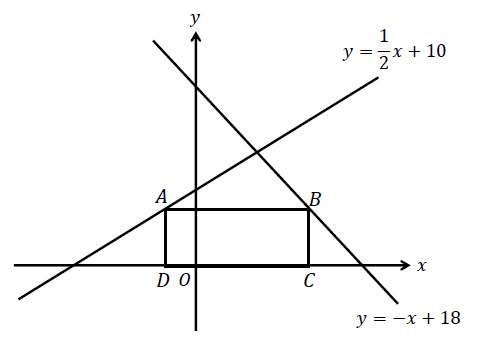
STEP1 文字を使って座標を表す
まずは求めたい点Aの\(x\)座標を文字でおきます。（今回は\(x=t\)として進めますね）
すると、点Aが通っている直線の式\(y=\frac{1}{2}x+10\) に代入すると\(y\)座標は\(\frac{1}{2}t+10\)と表すことができます。
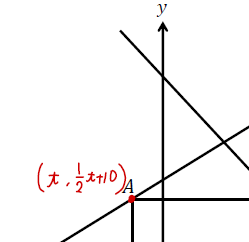
そこから真下に下ろした点D、真横にずらした点Bの座標も文字で表します。
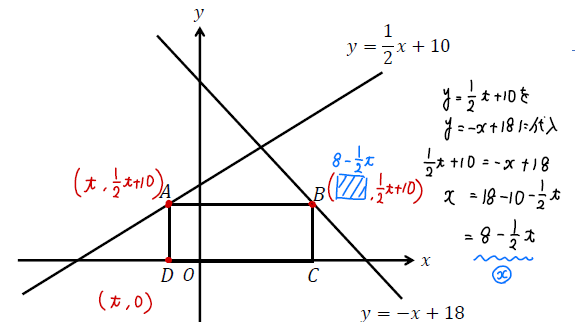
点Bを表すのがちょいムズですね(^^;)
点Aを真横にずらしただけなので、\(y\)座標は点Aと同じ\(\frac{1}{2}t+10\)となります。
そこから\(x\)座標を求めるため、\(y=\frac{1}{2}t+10\) を点Bを通る直線\(y=-x+18\)に代入して、\(x\)の方程式を解くと求めることができます。
この辺はちょっとややこしいので動画で計算手順を確認してもらえると理解がスムーズです＾＾
STEP2 辺の長さを表す
次に四角形の縦、横の長さを式で表していきましょう。
縦の長さADは点Ａ、Ｄの\(y\)座標どうしを引くと次のように求まります。
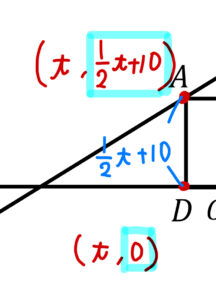
一方で、横の長さABは点A、Bの\(x\)座標を引くと次のようになります。
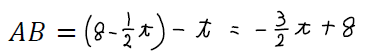
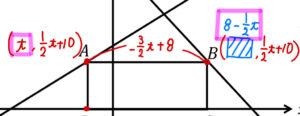
STEP3 辺の長さが等しいことから方程式をつくって解く
四角形が正方形になるということは
「縦の長さ ＝ 横の長さ」を満たすということ！
STEP2で求めた縦、横の長さを＝でつないで方程式を作って解いていきましょう。
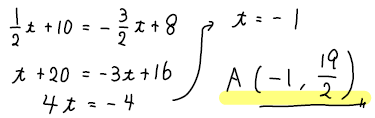
以上！
この3ステップで解いていけば正方形の座標は簡単に求まりますね＾＾
では、演習問題に挑戦して理解を深めていきましょう。
演習問題にチャレンジ！
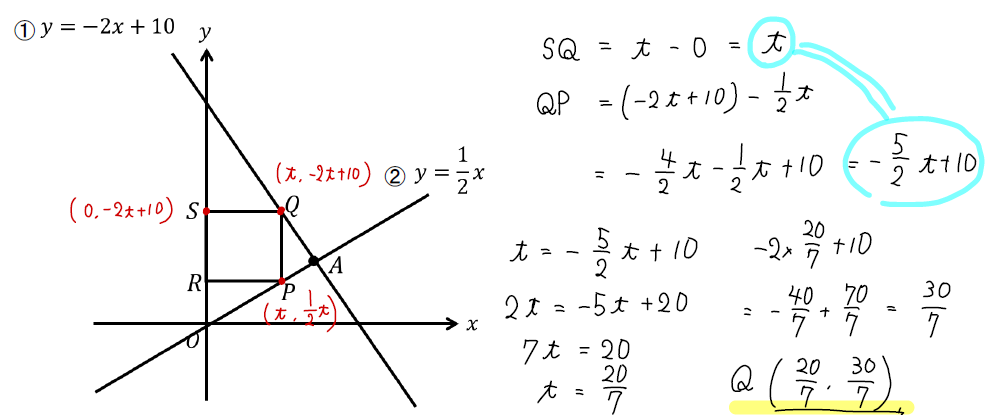
図のように線分OA上に点Pをとり、Pから\(y\)軸に平行となるようにひいた直線と直線①との交点をQとし、また、P、Qから\(x\)軸に平行となるようにひいた直線と\(y\)軸との交点をそれぞれR、Sとする。四角形PQSRが正方形になるとき、点Qの座標を求めなさい。
＼解説を動画でチェック／
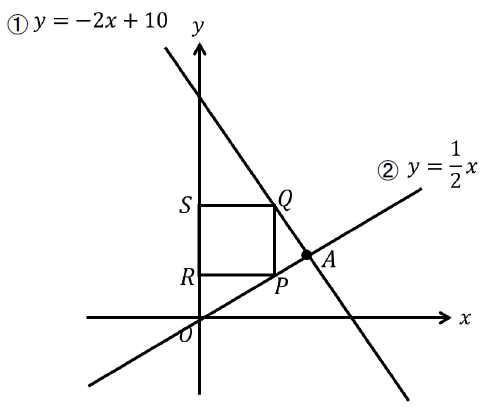
まとめ
お疲れ様でした！
今回の問題のポイントは「文字を使って座標、長さを表す」というところですね。
ここがスムーズになってくると、かなり応用力がUPすると思います＾＾
関数の入試演習にチャレンジしたい方は、こちらの記事がおススメ！
コメントを残す