【一次関数の利用】追いつく速さの文章問題を解説！

今回は中２で学習する一次関数の単元から

一次関数の利用である「追いつく速さ」の問題を取り上げて解説していきます。

追いつく利用問題では、大きく分けて2パターンの出題があります。

• ゴールまで一直線パターン

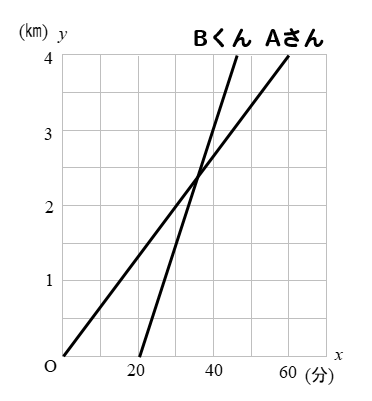
• 途中で休憩するパターン

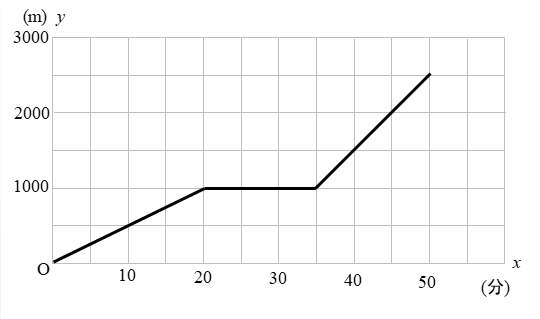
では、それぞれの問題の解き方を解説していきます(^^)

今回の問題はこちらの動画でも解説しています！

ゴールまで一直線　追いつく問題の解説！

まずは、ゴールまで一直線のパターンから見ていきましょう。

問題

自宅から4㎞離れた学校へ、Aさんは歩いて、Bくんは走って行った。グラフはそのときの時刻と自宅からの道のりの関係を示している。8時\(x\)分における家からの道のりを\(y\)kmとして、次の問いに答えなさい。

（1）Aさんについて\(x,y\)の関係を式に表しなさい。

（2）Bくんについて\(x,y\)の関係を式に表しなさい。

（3）BくんがAさんに追いついた時刻と場所を求めなさい。

切片が読み取れるグラフの式

Aさんのグラフを読み解いていきましょう。

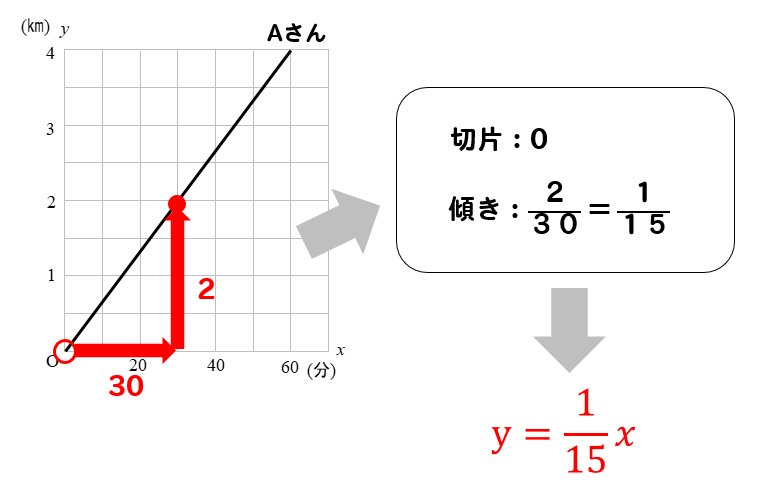
\(y\)軸との交点が切片でしたね。

ということで、切片は0。

グラフが30進んで、2上がっていることが読み取れるので

傾きは\(\displaystyle \frac{1}{15}\)となります。

よって、直線の式は\(\displaystyle y=\frac{1}{15}x\)です。

切片が読み取れないグラフの式

Bくんのグラフからは切片が読み取れません。

こういう場合には

• 2点の座標を読み取って、連立方程式を使用して式を導く方法

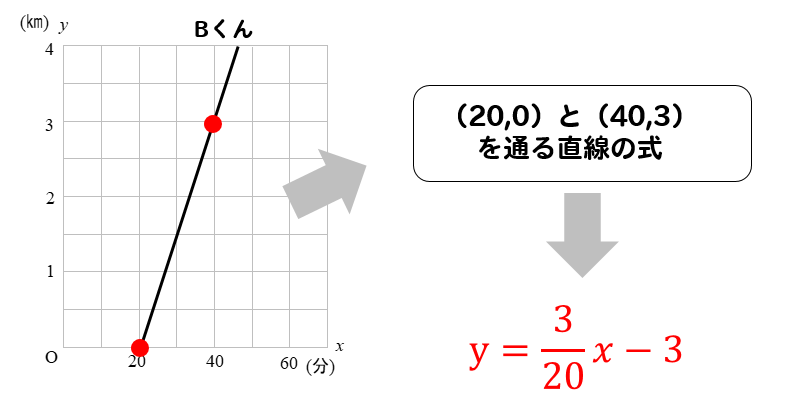
\((20,0)\)と\((40,3)\)を通ることから

それぞれ\(y=ax+b\)の式に当てはめて連立方程式を作ります。

$$\begin{eqnarray} \left\{ \begin{array}{l} 0 = 20a+b \\ 3 = 40a+b \end{array} \right. \end{eqnarray}$$

 

それぞれの式を引いて、加減法で解いていくと

$$3=20a$$

$$a=\frac{3}{20}$$

\(\displaystyle a=\frac{3}{20}\)を\(0=20a+b\)に代入すると

$$0=20\times \frac{3}{20}+b$$

$$0=3+b$$

$$b=-3$$

よって、\(\displaystyle y=\frac{3}{20}x-3\)となります。

• 傾きと1点の座標から式を導く方法

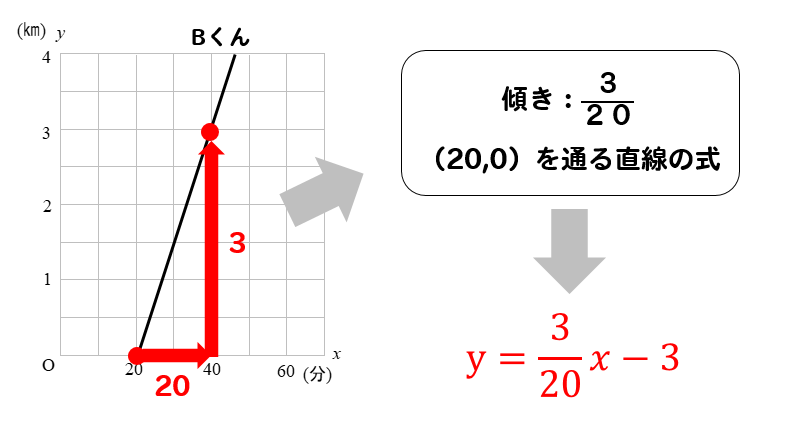
傾きが\(\displaystyle \frac{3}{20}\)ということから

$$y=\frac{3}{20}x+b$$

という式が作れます。

これに読み取った座標\(20,0\)を当てはめていきます。

$$0=\frac{3}{20}\times 20 +b$$

$$0=3+b$$

$$b=-3$$

よって、\(\displaystyle y=\frac{3}{20}x-3\)となります。

それぞれ、自分の合った方法で式を導いてください。

このように切片が分からない場合には、座標を読み取ることで式を作ることができます。

追いつく時間、場所を求める方法

2人が追いつくのは、グラフが交わるところになります。

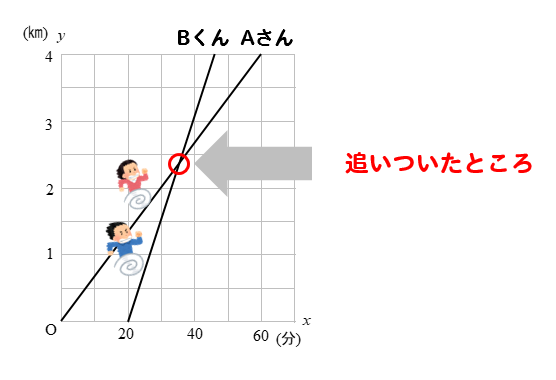
つまり、グラフの交点の座標が分かれば

2人の追いつく時間、場所を求めることができるわけです。

ここで思い出しておきたいのは

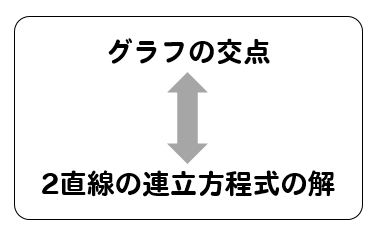
でしたね。

というわけで、先ほど求めた2人の式を連立方程式で解いていきましょう。

$$\begin{eqnarray} \left\{ \begin{array}{l} y = \frac{1}{15}x \\ y = \frac{3}{20}x-3 \end{array} \right. \end{eqnarray}$$

代入法で計算していきます。

$$\frac{1}{15}x=\frac{3}{20}x-3$$

分数の形を消すために両辺に60を掛けると

$$\frac{1}{15}x\times 60=\frac{3}{20}x\times 60-3\times 60$$

$$4x=9x-180$$

$$-5x=-180$$

$$x=36$$

\(x=36\)を\(\displaystyle y=\frac{1}{15}x\)に代入すると

$$y=\frac{1}{15}\times 36$$

$$y=\frac{12}{5}$$

よって

追いついた時刻は8時36分、場所は\(\displaystyle \frac{12}{5}\)kmの地点ということが分かりました。

途中で休憩する　追いつく問題の解説！

次は、途中で休憩するようなパターンを見ていきましょう。

問題

Aくんは、自宅を10時に出発し、途中、本屋に寄ってから図書館に行った。下の図は、Aくんが家を出てから\(x\)分後までに歩いた道のりを\(y\)mとして、図書館に着くまでの関係をグラフに表したものである。次の問いに答えなさい。

（1）家を出てから本屋までの分速を求めなさい。

（2）Aくんが本屋を出てから図書館に着くまでの\(x\)と\(y\)の関係を式に表しなさい。

（3）姉は10時35分に家を出て、自転車に乗って分速200mの速さで図書館に向かった。10時\(x\)分における家からの道のりを\(y\)mとして、家を出てから図書館に着くまでの\(x\)と\(y\)の関係をグラフにかき加えなさい。

（4）姉がA君に追いつく時刻と、家からの道のりを求めなさい。

なんか、グラフがカクカクしていて何を表しているのか分かりにくいですね。

まずは、このグラフの形から読み取れることを確認しておきましょう。

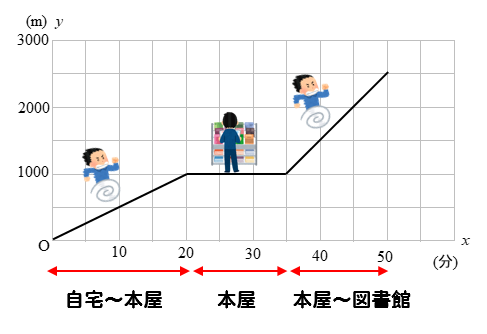
始めの直線は、自宅から本屋まで

真ん中の横線は、本屋に滞在していたところ

最後の直線は、本屋から図書館まで

をそれぞれ表しているんですね。

このことを理解した上で、それぞれの問題を確認していきましょう。

グラフから速さを求める

グラフから速さを求める場合には

何分で、どれくらいの距離を進んでいるのかを読み取りましょう。

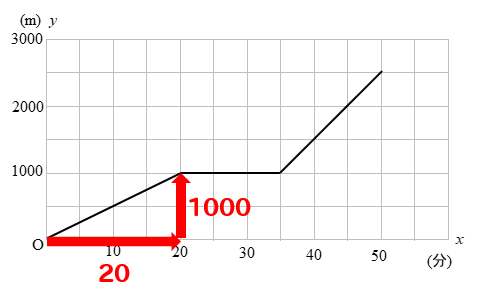
出発地点と本屋に到着した地点を比較してみると

20分で1000m進んでいるということがわかります。

ここから速さを計算していきます。

$$(速さ)=\frac{(道のり)}{(時間)}$$

であることを利用して

$$\frac{1000}{20}=50$$

よって、分速50mということが分かりました。

途中からの式を求める

本屋を出てから図書館に着くまでのグラフとは

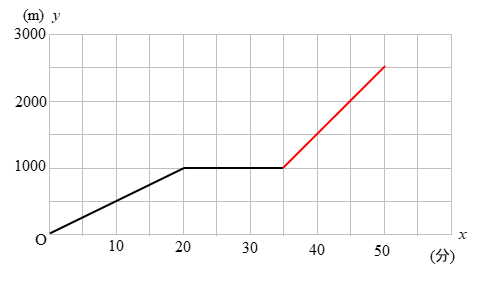
この赤い直線のことですね。

このように途中から始まっているようなグラフの式を作るときには

上の問題で紹介しているのと同様に、2つの座標を読み取って式を作っていきます。

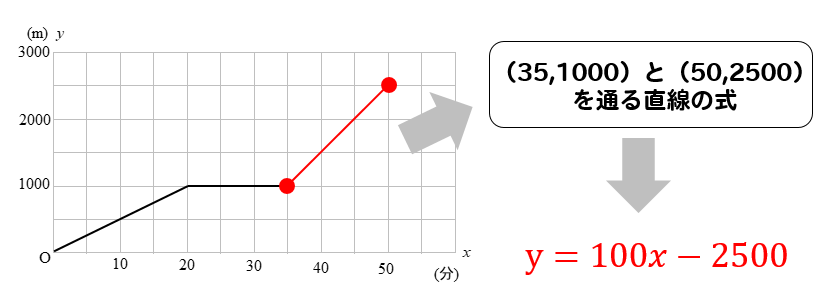
\((35,1000)\)と\((50,2500)\)を利用して計算していくと

直線の式は\(y=100x-2500\)となります。

直線の式を求めたいときには

とにかく2点の座標を読み取ってやればOKです。

グラフを書き込む

分速200mで進んでいるということから

1分間に200m進む⇒5分間に1000m進む

というように考えていくと

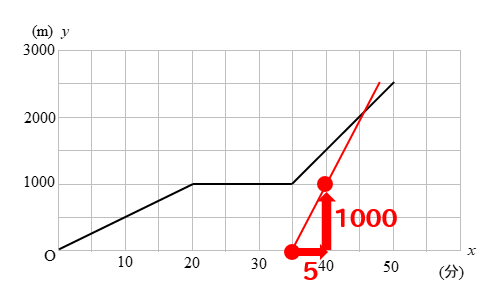
このようにグラフを書き込むことができます。

速さを、グラフの目盛りに合った数値に変換していくと

グラフが書き込みやすくなります(^^)

追いつく時刻と道のりを求める

Aくんのグラフと、先ほど書き込んだ姉のグラフとの交点を求めましょう。

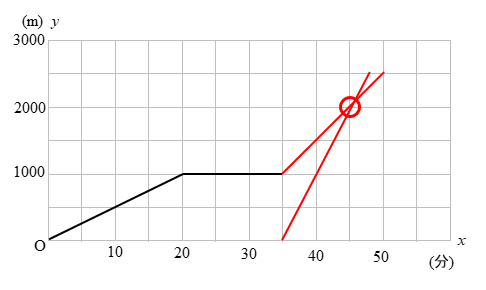
グラフを見ると、交点がぴったりと目盛り上にあるので

連立方程式を解かなくても交点を求めることができますね。

よって、姉がAくんに追いつく時刻は10時45分、追いついた場所は2000mの地点ということがわかりました。

もし、交点がぴったりと目盛り上にない場合には

姉の式を求めて、Aくんの式と連立方程式を作って計算していけば求めることができます。

グラフの交点をよく見て、すぐに読み取れそうならそのまま

読み取れないようであれば連立方程式へ

というように判断していってくださいね。

一次関数　追いつく問題まとめ

お疲れ様でした！

一次関数の追いつく問題では

• グラフから式を求めること
• グラフの交点を求めること

が必要となります。

一次関数の問題が苦手な人は

まず、式を作ったりグラフを書いたりする問題をマスターしてみましょう。

そうすれば応用問題であっても理解しやすくなるからね！