【確率】3人でじゃんけんするときの問題を解説！

今回は確率の単元から

3人でじゃんけんするときの確率問題について解説していきます。

取り上げる問題はこちら！

3人でじゃんけんすると何通り？

確率の問題では、まず

全部が何通りになるのか？がポイントですよね。

1人の手の出し方は

グー、チョキ、パーの3通りですね。

だから、2人でじゃんけんをするときには

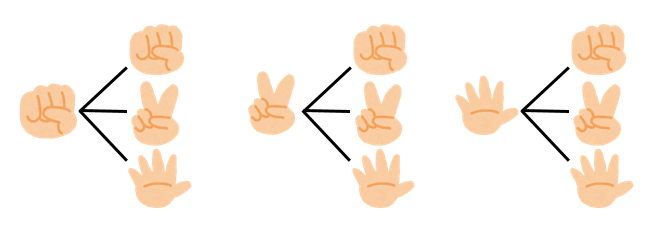
このように

$$\LARGE{3\times3=9(通り)}$$

になるということが分かりますね。

同じように考えると

3人でじゃんけんするときには

$$\LARGE{3\times3\times 3=27(通り)}$$

4人でじゃんけんするときには

$$\LARGE{3\times3\times 3\times 3=81(通り)}$$

こんな感じで全部で何通りかを求めることができます(^^)

それでは、これを利用して各問題を解いていきましょう！

（1）特定の1人だけが勝つ確率

Aだけが勝つというのは、次の状況が考えられます。

Aがグーを出して、他2人がチョキを出している。

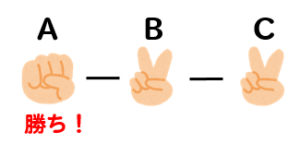
Aがチョキを出して、他2人がパーを出している。

Aがパーを出して、他2人がグーを出している。

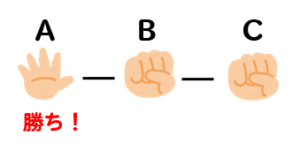
このようにAが勝つには

グーを出して勝つ場合

チョキを出して勝つ場合

パーを出して勝つ場合

以上、3通りあることがわかります。

よって、Aだけが勝つ確率は

$$\LARGE{\frac{3}{27}=\frac{1}{9}}$$

となります。

これは、Bだけが勝つ場合やCだけが勝つ場合でも同様になります。

とにかく3人でじゃんけんをしたときに特定の1人だけが勝つ確率は\(\displaystyle \frac{1}{9}\)となります。

（2）特定の人物が勝つ確率

Bが勝つ確率

この言葉には、少し引っかけ要素が含まれています。

Bが勝つというのは

「Bだけが勝つ」

とは違うからです。

とにかくBが勝っていれば良いので

こんな状況もアリになります。

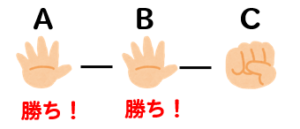
そういうことを考えるとBが勝つというのは以下の2パターンの状況があります。

• Bが1人勝ちする場合
• Bと誰かの2人勝ちする場合

Bが1人勝ちする場合の数は、（1）で求めたように3通りだとすぐに分かりますね。

それでは、Bと誰かの2人勝ちする場合が何通りあるのかを考えていきましょう。

2人勝ちのパターンとしては

AとBが勝つ場合とBとCが勝つ場合が考えられます。

まず、AとBが勝つ場合が全部で何通りあるか考えてみましょう。

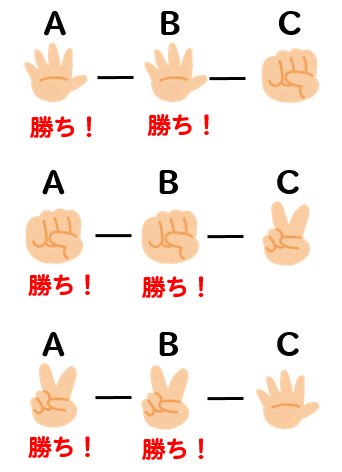
すると、このように3通りあることがわかりますね。

同様に考えるとBとCが勝つ場合も3通りであることが分かるので、それぞれを合わせるとBと誰かの2人勝ちするパターンは全部で6通りであることが求まりました。

よって、Bが勝つ場合は全部で

$$\large{3+6=9(通り)}$$

となります。

よって、Bが勝つ確率は

$$\LARGE{\frac{9}{27}=\frac{1}{3}}$$

ですね。

（3）あいこになる確率

あいこになるためには以下の状況が考えられます。

• 全員が同じ手を出した場合
• 全員が異なる手を出した場合

全員が同じ手を出して、あいこになる場合というのは

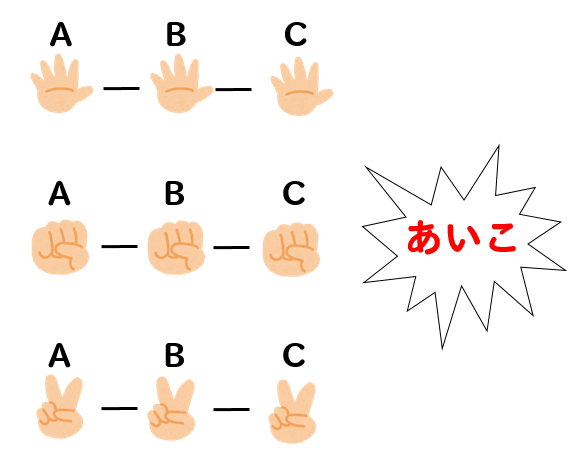
このように3通り考えることができますね。

次に、全員が異なる手を出してあいこになる場合を考えます。

Aがグーを出した場合

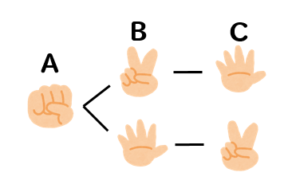
このように2通り考えることができます。

同様に考えると、Aがチョキ、パーを出した場合もそれぞれ2通りであることが分かります。

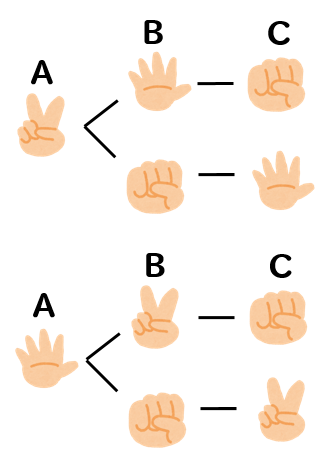
よって、全員が異なる手を出してあいこになる場合は全部で\(2\times 3=6\)通りとなります。

以上より、あいこになる場合の数は全部で

$$\large{3+6=9(通り)}$$

となるので、確率は

$$\LARGE{\frac{9}{27}=\frac{1}{3}}$$

となります。

テストに強くなる！確率の点を伸ばす定期対策ドリルをプレゼント！

お疲れ様でした＾＾

これでじゃんけんの確率のやり方は理解してもらえたと思います！

ただ、今回のようにさいころだけ、硬貨だけ、玉を取り出すだけ…のようにパターン別に演習をやっていると、頭を使うことなく流れで解けてしまうことが多いです。

実際のテストではどのパターンが出題されるかはランダムであり「表を使って考える？」「樹形図を使って考える？」といったことを問題文から解法を瞬時に判断していかないといけません。

というわけで！

今回は確率のテスト対策として、「問題⇒パッと解き方を判断」という特訓ができるような実戦演習を用意しました。

動画解説もつけているので苦手なお子さんでも1人で取り組めますよ＾＾

確率は他の単元に比べて、難しい公式、計算が出てこないので、数学をニガテにしている方でも点が伸ばしやすいです！なので、今回の課題も活用しながら、早めのテスト対策をしていきましょう(‘ω’)ノ

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

じゃんけんの確率は樹形図を使って考えてみるとラクにできましたね＾＾

問題で与えられた条件では、どのようなパターンが考えられるのか

それをしっかりと把握しながら進めていくことが大切です。

また

Aだけが勝つ確率

Aが勝つ確率

このように問題の出し方に少し引っかけが含まれているので、そこのところも注意しながら解いていきたいですね。