中3で学習する相似な図形の面積比!
苦手だなぁって思っている人も多い問題だよね…
この記事では、そんな面積比についてイチから問題の解き方を解説していきます。
記事を読み終えたあなたは…
面積比マスターだ!!
相似な図形の面積比
相似な図形の面積比は、相似比の2乗に等しくなるよ!
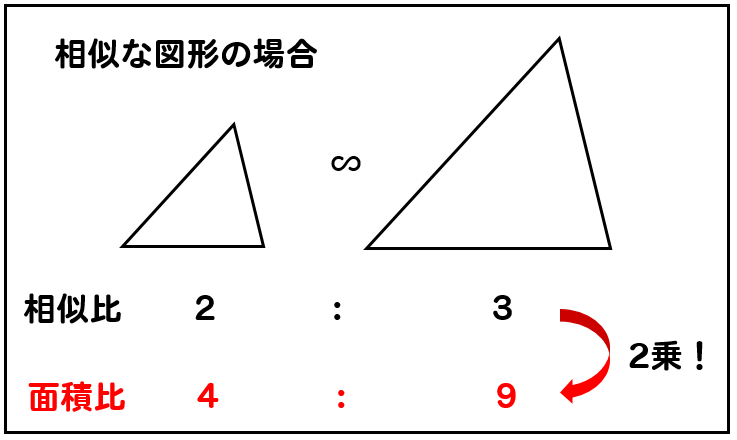
【例】
相似比:\(3:4\) ⇒2乗 面積比:\(9:16\)
相似比:\(5:6\) ⇒2乗 面積比:\(25:36\)
そして、面積比を考えるときには次のことも覚えておきたい!

このように、2つの三角形が相似でなかったとしても
高さが等しければ、底辺の比を見比べることで面積比を求めることができます。
相似なら、相似比の2乗!
相似でなくても高さが等しければ、底辺の比!
この2つのことをしっかりと覚えておいてください。
面積比を使った問題(基礎編)
【問題】
2つの相似な図形A、Bがあって、AとBの相似比が\(5:4\)である。図形Aの面積が\(100㎠\)のとき、図形Bの面積を求めなさい。
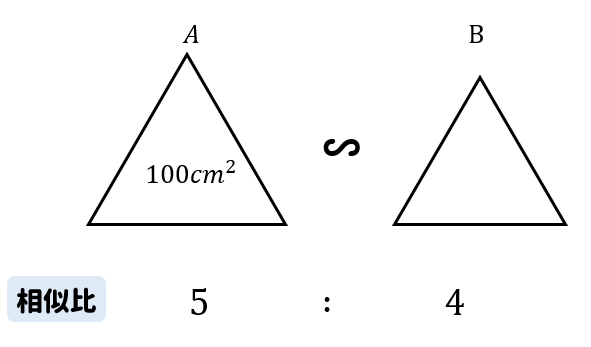
相似な図形の場合、相似比を2乗して面積比を作りましょう!
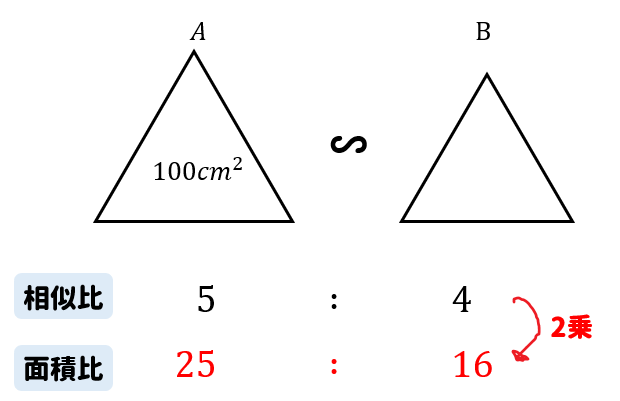
面積比が分かったら、あとは楽勝だね(^^)
図形Bの面積を\(x\)とおいて、比例式を作っていきましょう。
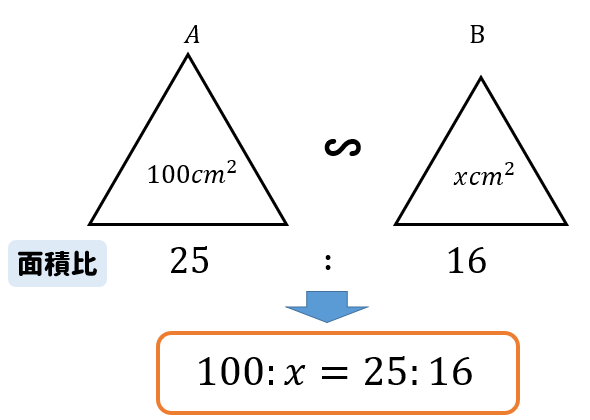
$$\begin{eqnarray}100:x&=&25:16\\[5pt]25x&=&1600\\[5pt]x&=&64 \end{eqnarray}$$
よって、図形Bの面積は\(64㎠\)となります。
相似比の2乗だ!ってことを覚えておけば簡単です(^^)
【問題】
次の図において、\(△ABD\)の面積が\(60㎠\)であるとき、\(△ADC\)の面積を求めなさい。
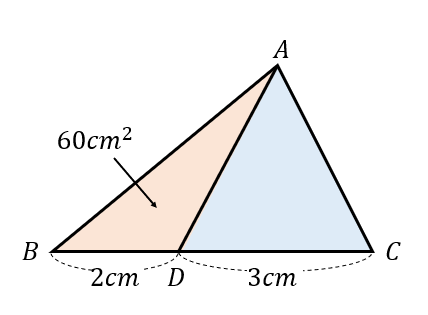
\(△ABD\)と\(△ADC\)は相似な図形にはなっていませんが、
2つとも高さが等しくなっていることに気が付きますか?
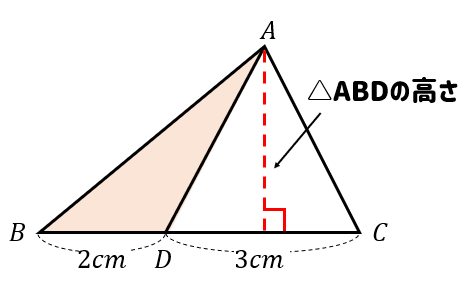
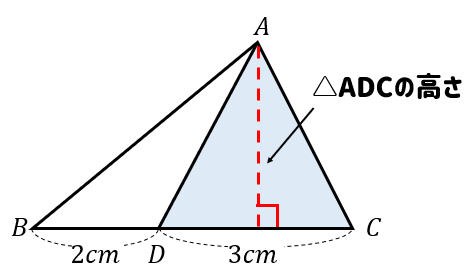
高さが同じだと分かれば
底辺の比がそのまま面積比となります。
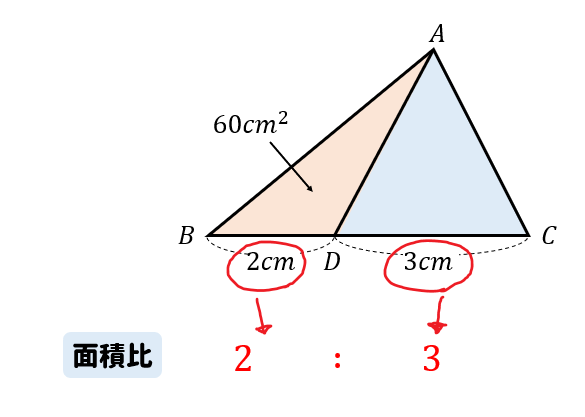
\(△ADC\)の面積を\(x\)として、比例式を作ると
$$\begin{eqnarray}60:x&=&2:3\\[5pt]2x&=&180\\[5pt]x&=&90 \end{eqnarray}$$
よって、\(△ADC\)の面積は\(90㎠\)となります。
面積比と聞かれたら、何でもかんでも2乗して面積比を作っちゃう人がいるので気を付けてくださいね。
2乗が使えるのは相似な図形のときだけ!
上の問題のように、同じ高さの三角形では底辺の比がそのまま面積比となるのでしっかりと覚えておきましょう!
基礎編についてはこちらの動画でも解説しています(/・ω・)/

面積比を使った問題(中級編)
【問題】
次の図で、\(DE//BC\)であるとき次の問いに答えなさい。
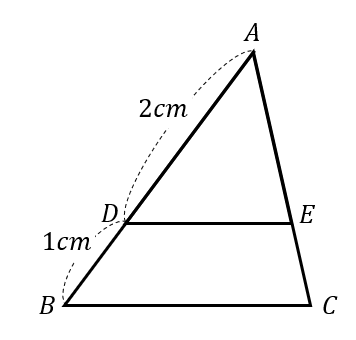
(1)\(△ABC\)と\(△ADE\)の面積比を求めなさい。
(2)\(△ADE\)と台形\(DBCE\)の面積比を求めなさい。
まず、\(△ABC\)と\(△ADE\)の面積比を考えたいのですが
図形が重なっていて分かりにくい…(^^;)
なので、このように別々に書いてあげると見やすくなりますね。
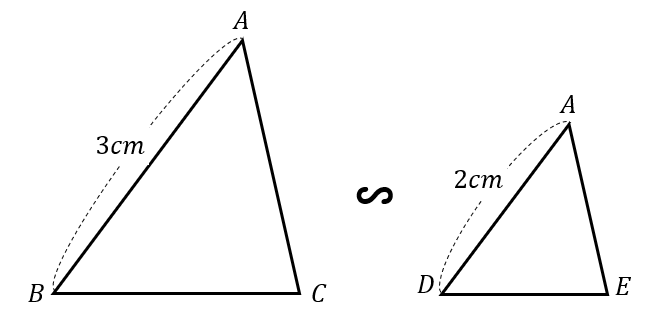
(\(AB\)の長さは2㎝と1㎝を合わせて3㎝になるね)
この2つの三角形は相似になっているので、相似比を2乗して面積比を考えましょう。
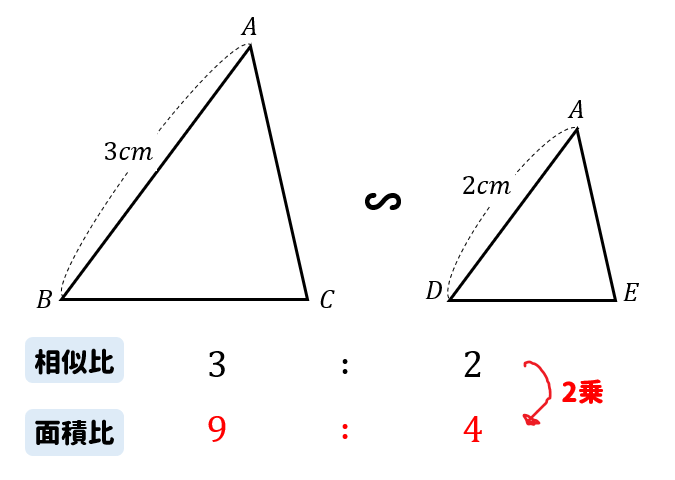
よって、\(△ABC\)と\(△ADE\)の面積比は\(9:4\)となります。
次に、\(△ADE\)と台形\(DBCE\)の面積比を考えてみましょう。
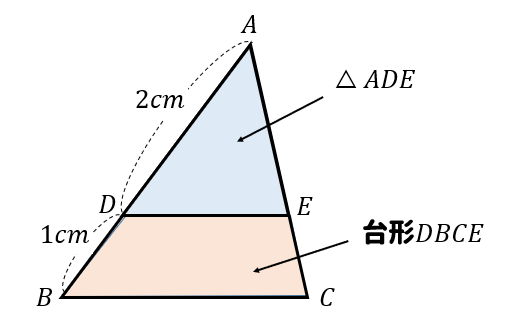
もちろんこの2つは相似な図形ではありませんので
相似比を利用するっていうのはできません。
ですが、(1)で求めた答えを利用すると簡単に求めることができます。
台形\(DBCE\)というのは、\(△ABC\)から\(△ADE\)を取り除いた図形になってることに気が付くかな?
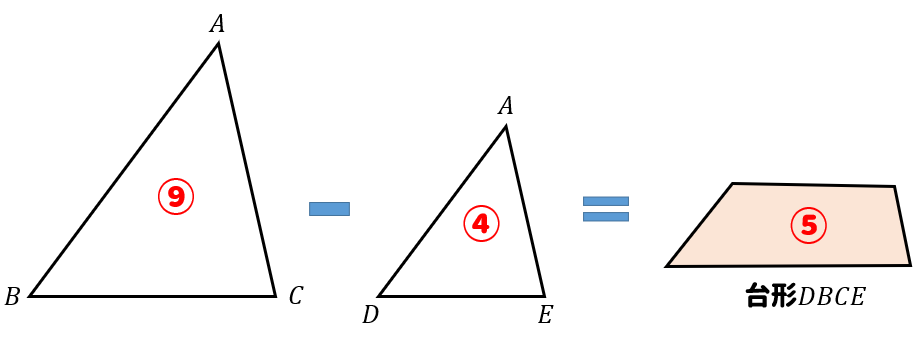
すると、2つの三角形の面積比が\(9:4\)だったことを利用して引き算をすると、台形の面積は⑤に相当することが分かりました。
よって、\(△ADE\)と台形\(DBCE\)の面積比は\(4:5\)となります。
中級編についてはこちらの動画でも解説しています(/・ω・)/
面積比を使った問題(応用編)
【問題】
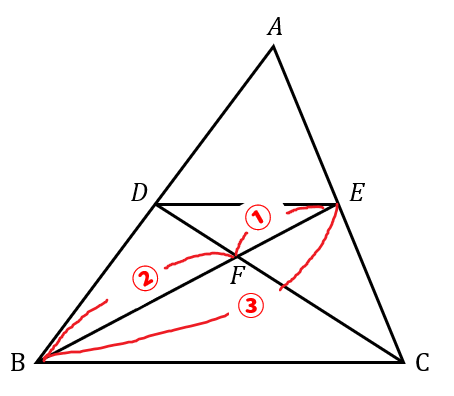
次の図において、\(AD=DB\)、\(AE=EC\)のとき、次の問いに答えなさい。
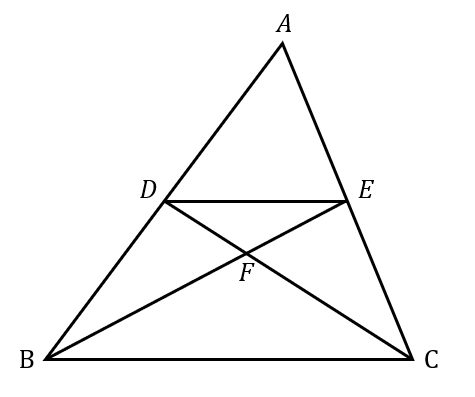
(1)\(△DEF\)と\(△BCF\)の面積比を求めなさい。
(2)\(△DEF\)と\(△BDE\)の面積比を求めなさい。
まず、今回の図形では中点\(D,E\)を結んでいることから
中点連結定理によって、\(DE//BC\)、\(DE:BC=1:2\)だと分かりますね。
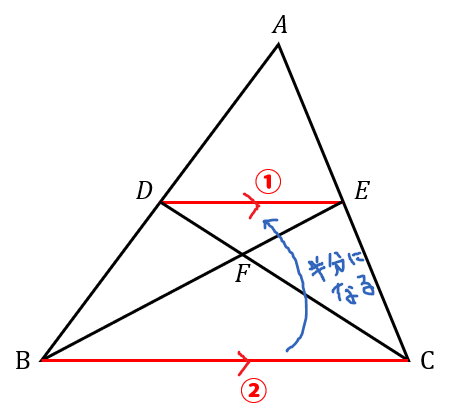
となると、\(△DEF\)と\(△BCF\)が相似であることが読み取れます。
更に、辺DEと辺BCの比から相似比が\(1:2\)と分かります。
よって、面積比は相似比を2乗して\(1:4\)となります。
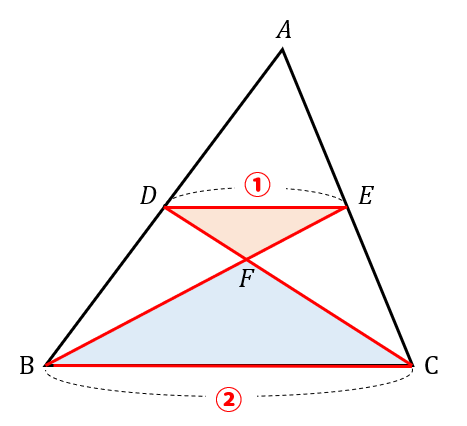
次に、\(△DEF\)と\(△BDE\)の面積比を考えましょう。
(1)で使った相似比から\(BF:EF=2:1\)になるので
\(BE:EF=3:1\)になることが分かります。
すると、\(△DEF\)と\(△BDE\)の三角形は、斜めになっているので分かりにくいですが、2つとも高さが同じ三角形になっています。
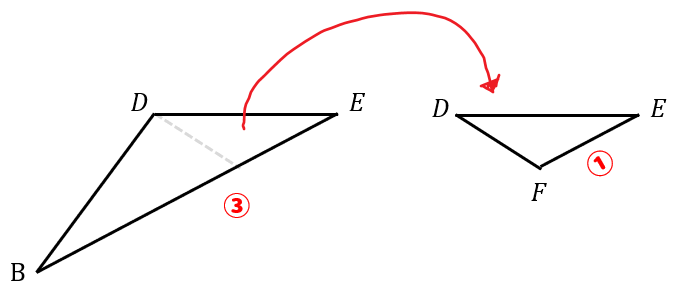
なので、底辺の比がそのまま面積比になるというわけです。
よって、\(△DEF\)と\(△BDE\)の面積比は\(1:3\)となります。
上級編についてはこちらの動画でも解説しています(/・ω・)/
他にも平行四辺形を使った相似比
台形を使った相似比などがあります。
まとめ!
お疲れ様でした!
面積比の問題って初めのうちは図形のどの部分を見ればいいいのか分からない…
ってなりますが、これは経験によって解決されます。
相似な図形のときには相似比の2乗


同じ高さの三角形は底辺の比


これらの性質を頭に入れた上で、たくさん問題を解いていきましょう!
ファイトだ(/・ω・)/
相似の面積比を求める問題をイチからやってみよう!←今回の記事




















コメントを残す