今回は小学校の算数で学習する
『円柱の体積の求め方』
について解説していくよ！
円柱の体積問題とはこんな感じのやつだね(^^)
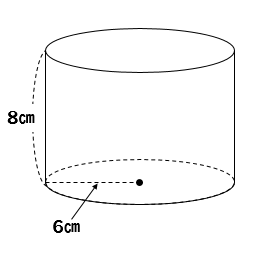
円…柱だと…！？
難しそうだ…
と、思ってしまいますが実はとっても簡単だよ！
しっかりと解き方を身につけていこう(/・ω・)/
円柱の体積公式！
まずは円柱の体積を求める公式をチェックしておこう！
たったコレだけのことだ！
シンプルだよね
円柱ってね
底面である円がたっくさん重なってできているっていう風に考えるんだ。
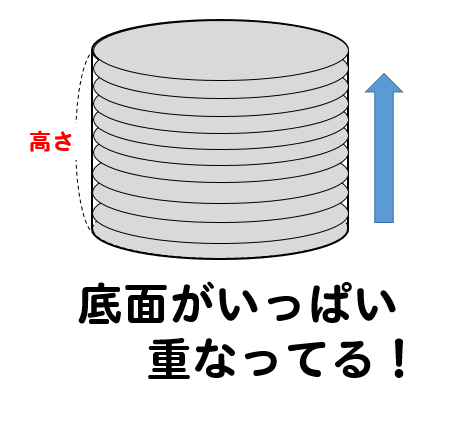
だから、全体の大きさである体積を知りたいと思えば
底面がどれくらい重なっているかを計算する。
つまり
底面積と高さをかければOKということになるよ！
この考え方を知っておけば
体積の公式もすぐに覚えれるね(^^)
あ、それと…
円柱の底面積を求めるためには、円の面積公式を覚えておく必要があるから思い出しておきましょう。
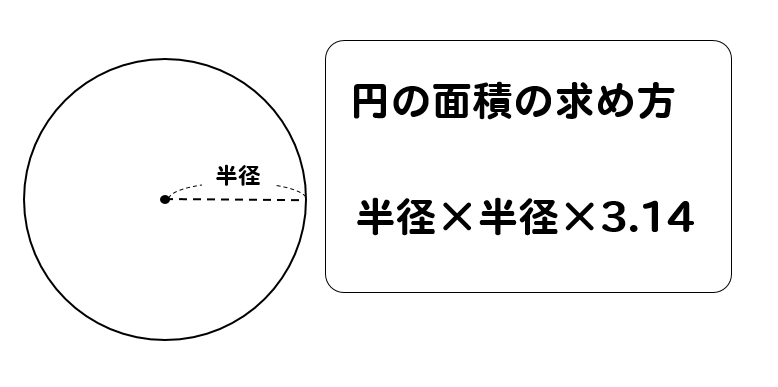
さぁ、これで円柱の体積を求めるための準備は整った！
問題に挑戦してみよう(/・ω・)/
円柱の体積求め方（小学生）
次の円柱の体積を求めましょう。
それでは、公式通り考えてみましょう。
まずは底面積を求めます。
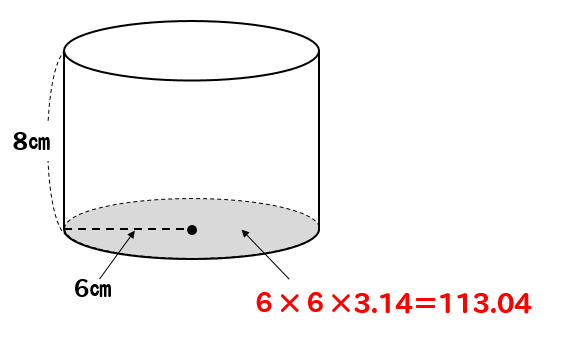
半径が6㎝なので
$$6\times 6\times 3.14=113.04(cm^2)$$
となりますね。
（ちょっと数字がデカいな…(^^;）
底面積が求まれば、あとは高さをかけるだけ！
$$\Large{113.04\times 8=904.32(cm^3)}$$
となりました！
どうでしたか？
途中の計算はめんどうだったかもしれませんが
考え方や解き方は難しくありませんね！
底面積を求めて、高さをかけるだけ！
それでは、円柱の体積問題をバッチリにするため演習問題に挑戦してみましょう！
円柱の演習問題（小学生）
次の円柱の体積を求めましょう。
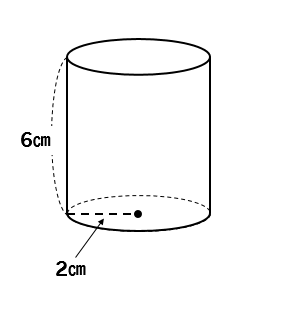
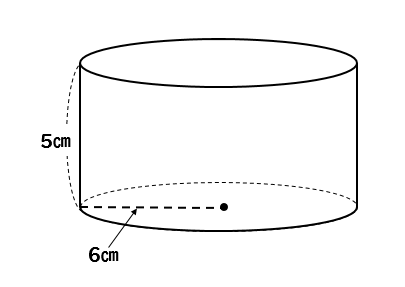
次の円柱の体積を求めましょう。
まとめ
お疲れ様でした！
これで円柱の体積はバッチリかな？
円柱の体積はね、中学生になっても学習するし
高校入試にも必須の問題になるんだよ！
だから、今のうちにしっかりとマスターしておきたいところだね(^^)
さぁ、あとは学校の計算ドリルなどを使って練習あるのみだ(/・ω・)/
がんばっているのに60点の壁をクリアできない中3生の方へ
頑張っているのに思うように成績が上がらず、
「このままだと本番で数学60点が厳しいかも…」
と不安に感じているあなた。
もしかして、
このような問題に直面していませんか？
- 模試になると点がガクッと落ちる
- 復習のやり方が分からない
- 勉強してもすぐに忘れる
- 凡ミスが直らない
- 家だと集中して勉強できない
- 問題集を買っても、1人で解けなくて途中でやめてしまう
- 友人が点を伸ばしていて焦る
- 頑張りたいから何をすればいいか教えて欲しい
僕が2年前に指導させてもらった中3のAくん
彼がまさにこのような状態でした。
すごく勉強したのに試験の結果が36点…
「どうすればいいか分からない…」
「点を上げれる自信がない…」
自信をなくし落ち込んでいましたが、
ある勉強方法を取り入れたことによって
Aくんは大変身！
なんと、たった2ヶ月で
36点 ⇒ 72点
なんと、驚きの36点UPを達成！
何をやっても点が伸びなかったAくん
彼を大変身させた「ある勉強方法」とは、
たったの3分で取り組める簡単なものです。
この勉強法を活用した人は、
43点 ⇒ 69点
67点 ⇒ 94点
人生初の100点！
このように次々と良い結果を報告してくれています＾＾
Aくんを大変身させた「ある勉強法」を
あなたにも活用してもらい
今すぐにでも結果を出して欲しいです。
そこで！
ある勉強法を正しく身につけてもらうための
1週間の集中メルマガ講座を作成しました。
こちらのメルマガ講座の中で、
順にワークをお渡ししていくので1つずつ取り組み、
やればやっただけ点が伸びていく感覚を掴んでくださいね！
もちろんこの講座の登録は無料！
いますぐワークを受け取っておきましょう('◇')ゞ
コメントを残す