今回の記事では、
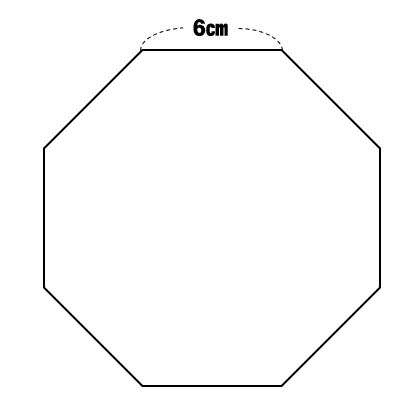
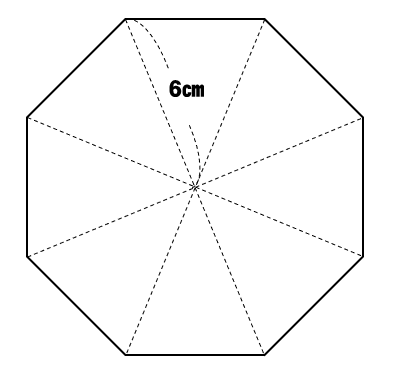
上のような2パターンの正八角形の面積を求める方法について解説していきます。
この問題を解くためには中学3年生で学習する「三平方の定理」の知識が必要となります。
1辺の長さが6㎝の正八角形の面積
【問題】
1辺が6㎝の正八角形の面積を求めなさい。
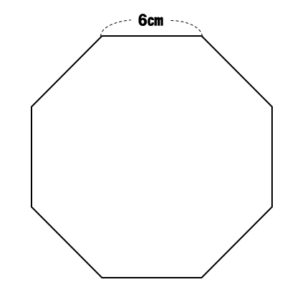
考え方を身につけてしまえば簡単に解くことができるようになります!
まずは、このように正方形を作りましょう。
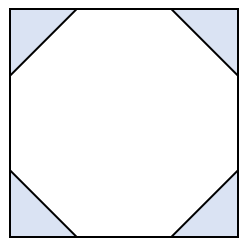
そして、正方形から四隅にある三角形を4つ分引いてあげればOK。
と、考えていきましょう。
正八角形の外角が45°であることを考えると
四隅にある三角形は45°、45°、90°になっている特別な直角三角形であることが分かりますね。
だから、辺の比は \(1:1:\sqrt{2}\) となるので
このように辺の長さを求めることができます。
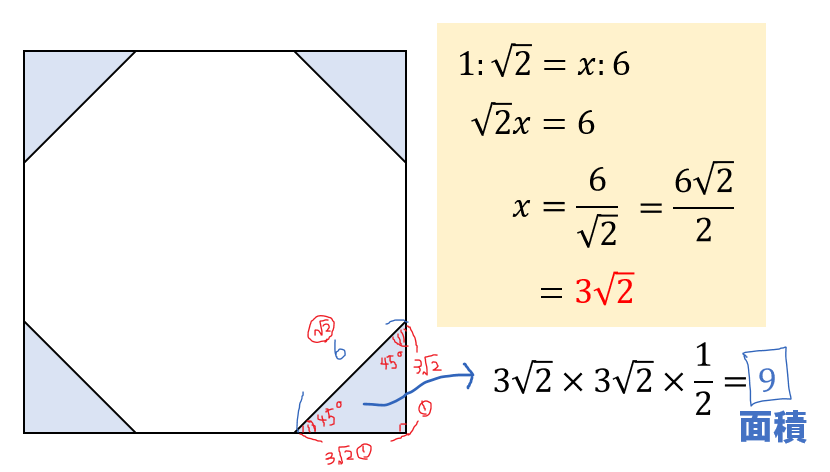
すると、このように三角形の面積も求まります。
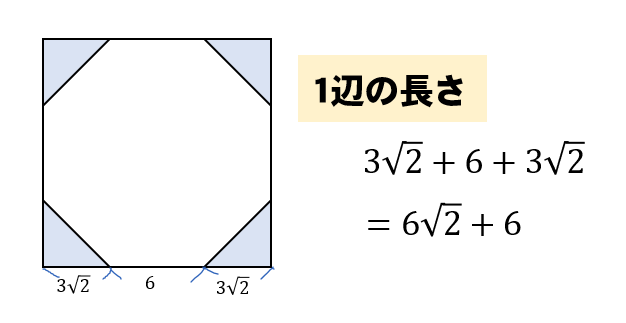
次に、正方形の1辺の長さを考えると
\(3\sqrt{2}+6+3\sqrt{2}=6+6\sqrt{2}\)となるので
正方形の面積は、
$$\begin{eqnarray}(6+6\sqrt{2})\times (6+6\sqrt{2})=(6+6\sqrt{2})^2 \end{eqnarray}$$
となります。
よって、最後に正方形から三角形4つ分を引いてあげれば完成。
$$\begin{eqnarray}&&(6+6\sqrt{2})^2-9\times 4\\[5pt]&=&36+72\sqrt{2}+72-36\\[5pt]&=&72\sqrt{2}+72\cdots(解) \end{eqnarray}$$
答え
$$72\sqrt{2}+72(cm^2)$$
半径6㎝の円に内接する正八角形の面積
【問題】
次の正八角形の面積を求めなさい。
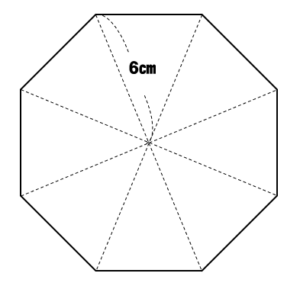
正八角形の中に二等辺三角形が8つ分できてることに気が付きますね。
なので、二等辺三角形の面積を求めて、それを8つ分にする。
という考え方で正八角形の面積を求めていきます。
中心の360°を8等分していることから
二等辺三角形の頂角は\(360\div 8=45°\) であることが分かりますね。
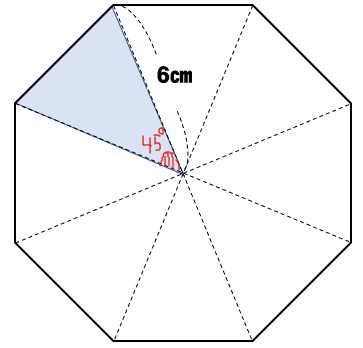
そして、次のように補助線を引くと
45°、45°、90°の直角三角形が作れます。
よって、二等辺三角形の高さにあたる辺の長さを求めることができます。
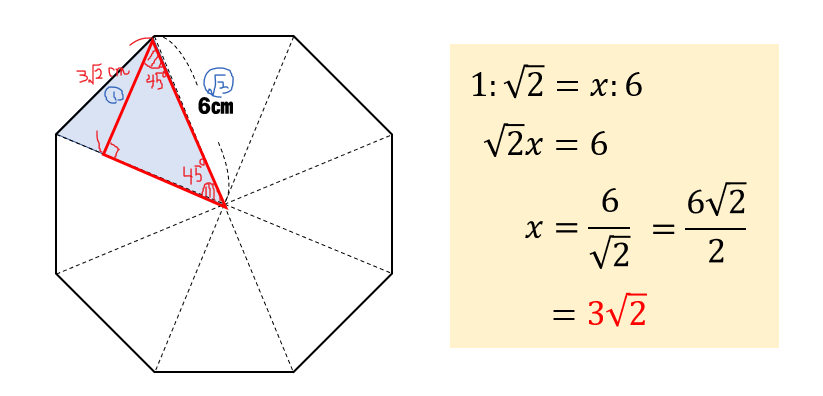
よって、二等辺三角形の面積は
$$\begin{eqnarray}6\times 3\sqrt{2}\times \frac{1}{2}=9\sqrt{2} \end{eqnarray}$$
となります。
正八角形は、この二等辺三角形が8つ分の大きさだから
$$\begin{eqnarray}9\sqrt{2}\times 8=72\sqrt{2}(cm^2) \end{eqnarray}$$
となりました。
答え
$$72\sqrt{2}(cm^2)$$
まとめ!
お疲れ様でした!
ちょっと発想は難しいかもしれませんが、
一度解いたことがある人にとっては楽勝な問題になりますね。
なので、今回の記事を通して
正八角形の面積についてはしっかりとインプットしておいてくださいね(/・ω・)/

















コメントを残す