高校数学Ⅱで学習する「微分」の単元から
平均変化率の求め方
についてサクッと解説していきます。
平均変化率の公式とは、次のようなものです。
関数\(y=f(x)\)において、\(x\)の値が\(a\)から\(b\)まで変化するとき
$$\frac{f(b)-f(a)}{b-a}$$
を\(x=a \)から\(x=b \)までの、\(f(x)\)の平均変化率という。
この説明だけ見て、どうかな…？
式が難しく見えちゃって、何を言ってるのかマジ不明！
って感じだね(^^;)
というわけで、今回の記事では
そんな平均変化率の問題について
あ、こんなに簡単なことなのか！
と思ってもらえるように解き方を解説していきます。
平均変化率の求め方
平均変化率？
なんじゃそりゃ…って思っている方も多いと思います。
ですが、実は中学の時に「変化の割合」という名前で一度習っているんですよ！
つまり、平均変化率と変化の割合は同じ求め方ってことになります。
変化の割合とは
このように、それぞれの増加量を割ったモノでしたね。
これをかっこよく式で表したもの
それが平均変化率の公式ってことになります。
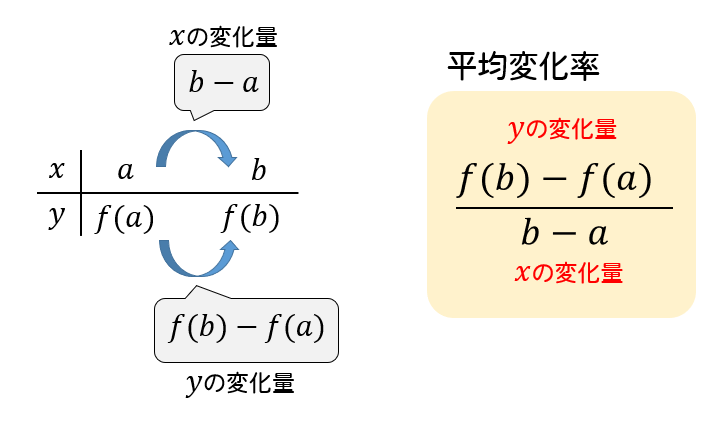
なので、完全に新しいことをやるってわけではないので
あまり難しく考えないようにしてくださいね(^^)
では、実際に問題の解き方を確認してみましょう！
【問題】
関数\(f(x)＝x^2\)において、\(x\)の値が\(1\)から\(3\)まで変化するときの平均変化率を求めなさい。
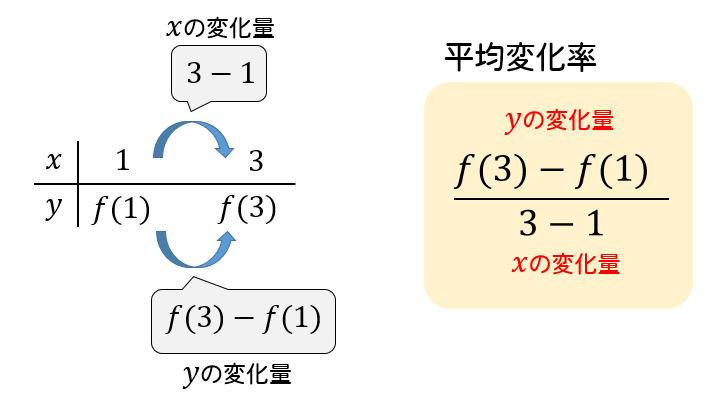
\(f(1)\)っていうのは、\(f(x)=x^2\)に\(x=1\)を代入した値のことですね。
だから、\(f(1)=1^2=1\)となります。
同じように、\(f(3)=3^2=9\)。
よって、平均変化率は
$$\begin{eqnarray}\frac{f(3)-f(1)}{3-1}&=&\frac{9-1}{2}\\[5pt]&=&4\cdots(解) \end{eqnarray}$$
となります。
簡単ですね(^^)
では、少しずつ複雑にしていきましょう。
【問題】
関数\(f(x)＝x^2-5x\)において、\(x\)の値が\(1\)から\(1+h\)まで変化するときの平均変化率を求めなさい。
\(1+h\)！？
となってしまいそうですが、やり方は同じです。
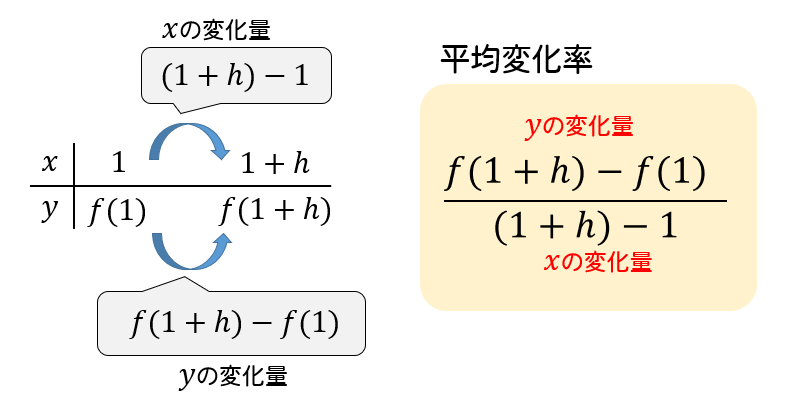
式が複雑に見えますが、形としては同じだよね！
$$f(1)=1^2-5\times 1=1-5=-4$$
$$\begin{eqnarray}f(1+h)&=&(1+h)^2-5(1+h)\\[5pt]&=&1+2h+h^2-5-5h=h^2-3h-4 \end{eqnarray}$$
よって、平均変化率は
$$\begin{eqnarray}\frac{f(1+h)-f(1)}{(1+h)-1}&=&\frac{(h^2-3h-4)-(-4)}{h}\\[5pt]&=&\frac{h^2-3h}{h}\\[5pt]&=&h-3\cdots(解) \end{eqnarray}$$
ちょっと計算がめんどうではありますが
やり方が分からないってことはないですね！
まとめ！
お疲れ様でした！
平均変化率は、公式の見た目が難しそうではありますが
実際にやってることは至ってシンプル
\(x,y\)の変化量を求めて割ってるだけですね。
ただ、\(1+h\)などの値を考える場合には
計算量が多くなっちゃうので、
ミスをしないように途中式をていねいに書いて計算しましょう！
今の状況に不安を感じている方は…
コロナの影響によって、多くの学校がお休みになっている状況。
休みが増えてラッキー！
と感じている一方で、心の奥底では…
このままで勉強は大丈夫なのだろうか。
受験までに学力を伸ばせるのだろうか。
ライバルたちはどうやって対策しているのだろうか。
このような不安を感じている方もいるでしょう。
そんなあなたには
スタディサプリを使うことをおススメします。
スタディサプリを使うことで、
学校や学習塾で学べる内容を自宅にいながらサクッと学ぶことができます。
勉強を頑張りたい気持ちはあるけど、
何をどうすればいいのか…？
そういった悩みに対しても、スタディサプリで解決できます。
スタディサプリでは学習レベルに合わせて授業を進めることが出来るほか、たくさんの問題演習も行えるようになっています。
スタディサプリが提供するカリキュラム通りに学習を進めていくことで
何をしたらよいのか分からない…
といったムダな悩みに時間を割くことなく
ひたすら学習に打ち込むことができるようになります(^^)
また、スタディサプリにはこのようなたくさんのメリットがあります。
- 費用が安い！月額1980円で全教科全講義が見放題です。
- 基礎から応用まで各レベルに合わせた講義が受けれる
- 教科書に対応！それぞれの教科に沿って学習を進めることができる
- いつでもどこでも受講できる。時間や場所を選ばず受講できます。
- プロ講師の授業はていねいで分かりやすい！
- 都道府県別の受験対策もバッチリ！
- 合わないと感じれば、すぐに解約できる。
スタディサプリを活用することによって
学校が再開したときには、ライバルたちと差を広げることができます。
「最近、成績が上がってきてるけど塾でも通い始めたの？」
「どんなテキスト使ってるのか教えて！」
「勉強教えてーー！！」
スタディサプリを活用することで
どんどん成績が上がり
友達から羨ましがられることでしょう(^^)
今まで通りの学習方法に不満のない方は、スタディサプリを使わなくても良いのですが
学習の成果を高めて、効率よく成績を上げていきたい方
是非、スタディサプリを活用してみてください。
スタディサプリでは、14日間の無料体験を受けることができます。
まずは無料体験受講をしてみましょう！
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
スタディサプリ小・中学講座
スタディサプリ高校講座
