【関数y=ax2乗】式の作り方はこれでバッチリ！aの値の求め方とは？

今回は中3で学習する『\(y\)は\(x\)の二乗に比例する関数』という単元から、\(y=ax^2\)の式の作り方について解説していくよ！

式を作る問題は大きく分けて3つのパターンがあります。

• 文章から式を作る
• 表から読み取って式を作る
• グラフから読み取って式を作る

それでは、それぞれの問題を見ていきましょう！

今回の記事は、こちらの動画でも解説しています(/・ω・)/

文章からy=ax2の式を作る

式を作るためには、式の形を覚えておく必要があります。

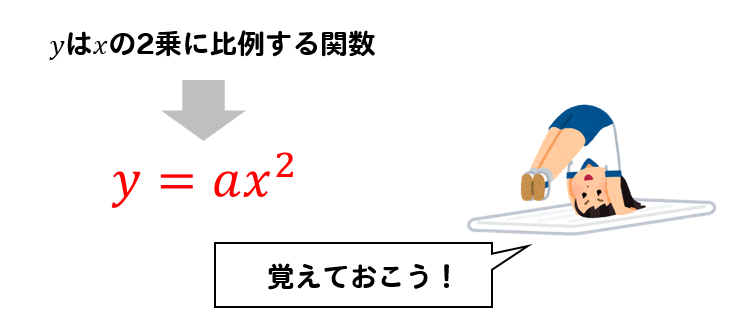
\(y=ax^2\)の式に、問題で与えられている\(x=3\)と\(y=27\)を代入しましょう。

すると

$$27=a\times 3^2$$

$$27=9a$$

$$a=3$$

となり、比例定数\(a\)が3であることが求まりました。

よって、式は

$$\Large{y=3x^2}$$

となり、完成です！

簡単でしたね(^^)

\(y=ax^2\)の形を覚えておけば、あとは代入して\(a\)の値を求めるだけです。

それでは、\(y=3x^2\)という式を使って更なる問題に挑戦してみましょうか。

\(x,y\)の値を求める問題では、与えられている文字の値を代入するだけで求めることができます。

\(x\)の値を代入すれば\(y\)の値が求まる

\(y\)の値を代入すれば\(x\)の値が求まる

といった感じです。

それでは、まず（1）の問題を見ていきます。

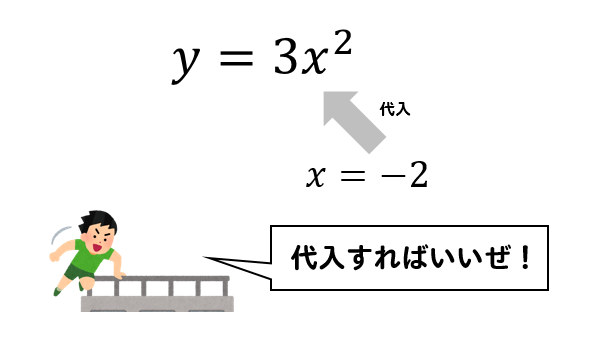
\(x=-2\)を代入すればいいので

$$y=3\times (-2)^2$$

$$=3\times 4$$

$$y=12$$

となります。

（2）も同様に代入していきましょう。

\(y=75\)を代入すればいいので

$$75=3x^2$$

$$25=x^2$$

$$x=\pm 5$$

となります。

最後は、二次方程式の知識を用いて解くことになるので、不安な方はこちらの記事もチェックしておいてくださいね

【二次方程式】問題の解説付き！解き方をパターン別に説明していくよ！

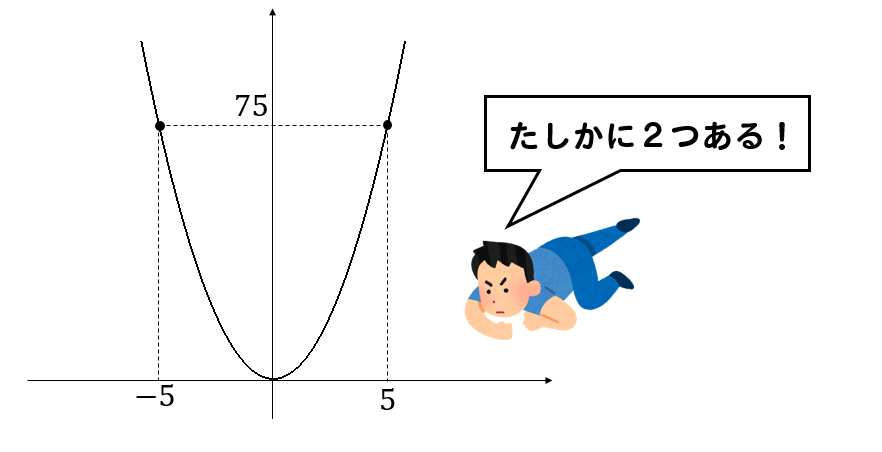
\(y\)は\(x\)の2乗に比例する関数では、\(y\)の値を1つ決めると\(x\)の値が2つ決まるっていうのがポイントですね。（０の場合は1つになっちゃうけど）

それでは、練習問題に挑戦して理解を深めていきましょう。

練習問題に挑戦！

表からy=ax2の式を作る

関数\(y=ax^2\)について、\(x,y\)の関係が下の表のようになるとき、次の問いに答えなさい。

（1）この関数の式を求めなさい。

（2）表の空欄部分を埋めなさい。

表から式を作るときには、\(x,y\)ともに値がそろっているところに注目しましょう！

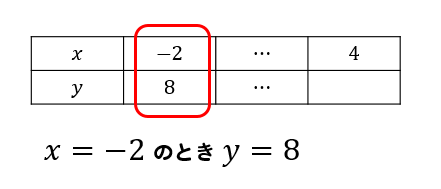
すると、この関数は\(x=-2\)のとき\(y=8\)であるということが読み取れます。

この情報が読み取れれば、先ほど解いた問題と同じことだと気づきますね(^^)

\(y=ax^2\)に\(x=-2\)と\(y=8\)を代入すると

$$8=a\times (-2)^2$$

$$8=4a$$

$$a=2$$

よって

$$\Large{y=2x^2}$$

となります。

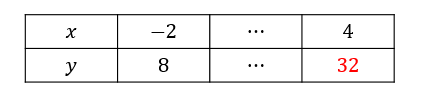
次に空欄を埋めていきますが

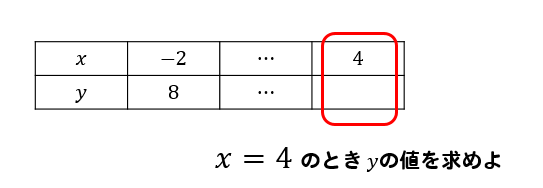
こちらは\(x=4\)のとき\(y\)の値は何になるか？という問題と同じですね

先ほど求めた\(y=2x^2\)に\(x=4\)を代入すると

$$y=2\times 4^2$$

$$=2\times 16$$

$$=32$$

となります。

練習問題に挑戦！

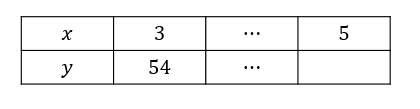
関数\(y=ax^2\)について、\(x,y\)の関係が下の表のようになるとき、次の問いに答えなさい。

（1）この関数の式を求めなさい。

（2）表の空欄部分を埋めなさい。

グラフからy=ax2の式を作る

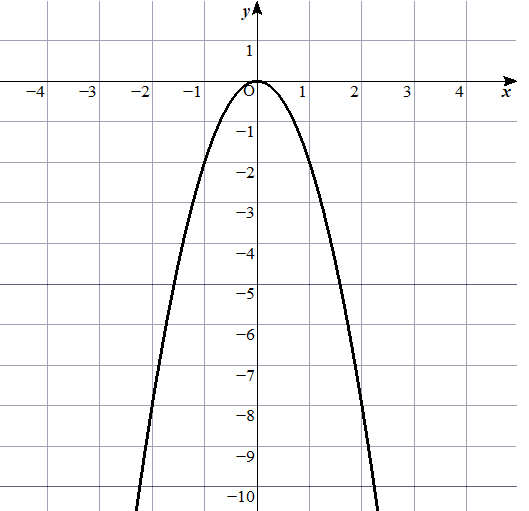
次のグラフの式を求めなさい。

グラフから式を求める場合には

どこでもいいので１つ座標を読み取ろう！

このグラフからは\((2,2)\)という座標が読み取れますね。

もちろんこれ以外に\((4,8)\)や\((-2,4)\)といった座標でもOKです！

グラフが\((2,2)\)を通るということは

\(x=2\)のとき\(y=2\)になるということです。

ここまで読み取ることができれば、この記事でさんざん練習している通りの方法で求めることができますね(^^)

\(y=ax^2\)に\(x=2\)と\(y=2\)を代入してやると

$$2=a\times 2^2$$

$$2=4a$$

$$a=\frac{1}{2}$$

よって、式は

$$\Large{y=\frac{1}{2}x^2}$$

となります。

グラフから式を求めるときには

座標を読み取る！

これだけですね(^^)

練習問題に挑戦！

次のグラフの式を求めなさい。

y=ax2の式　まとめ

お疲れ様でした！

様々なパターンの問題を解説しましたが

基本的な部分ではどれも同じでしたね。

$$\Large{y=ax^2}$$

この式に代入！

これをマスターするだけで大丈夫です(^^)

簡単♪簡単♪