【二次方程式】問題の解説付き！解き方をパターン別に説明していくよ！

今回は中３で学習する『二次方程式』の解き方について、パターン別に解説付きで説明をしていくよ！

今回、取り上げるのは以下の問題です。

これらが解けるようになったら、最後には入試問題から抜粋した練習問題を用意しているから挑戦してみよう！

二次方程式の解き方を瞬時に判断するコツについて、こちらの動画で解説しています！

問題を解く前にチェックしておくと知識が整理されて、学びの効果がアップしますよ＾＾

(1)(2)の解説！平方根の考え方を利用する

二次方程式の式を見て

$$x^2= 数$$

$$(xの式)^2 = 数$$

の形になっていたら、平方根の考え方を利用して解いていきましょう。

平方根の考え方を利用すると、次のように

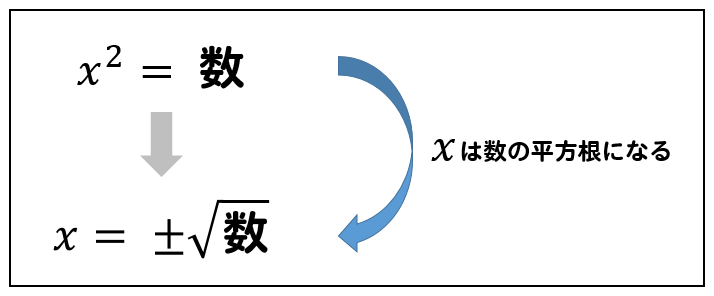
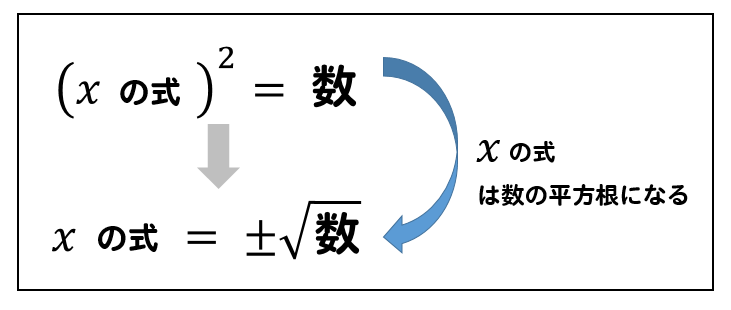
『二乗をとって、数に±ルートをつける』

という変形をしていけば良いのでしたね！

詳しくはこちらの記事をご参考ください。

＞＞＞【二次方程式】平方根の考えを使った解き方を解説！

それでは、（1）（2）の解き方について、それぞれ見ていきましょう。

（1）の解説！

二乗をとって、±ルートをつければ良いので

$$x^2=5$$

$$x=\pm \sqrt{5}$$

と、なります。

ルートの中身が簡単に出来る場合は、忘れないように簡単にしておきましょうね！

$\sqrt{5}$は、これ以上簡単にできないのでこれで終わり！

簡単でしたね(^^)

（2）の解説！

こちらも先ほどと同様に、二乗をとって±ルートをつけていきます。

$$(x+6)^2=12$$

$$x+6=\pm \sqrt{12}$$

$$x=-6\pm 2\sqrt{3}$$

ルートの中身を外に出せるので、忘れないように！

(3)(4)の解説！因数分解を利用した解き方！

二次方程式の式を変形して

A×B＝０

という形にできる場合には、因数分解を利用した解き方を使います。

A×B＝0　の形で表せる場合

A＝0　または　B=0　になるという特徴がありましたね。

この特徴を利用して、二次方程式を解いていきます。

詳しくはこちらの記事で解説しています。

＞＞＞【二次方程式】因数分解を利用した解き方を解説！

（3）の解説！

$(3x-2)$と$(x+5)$を掛けると0になるということから

$3x-2=0$もしくは$x+5=0$になるということが分かります。

よって

$$3x-2=0$$

$$3x=2$$

$$x=\frac{2}{3}$$

$$x+5=0$$

$$x=-5$$

（4）の解説！

見たところA×B＝0に形になっていないのですが、因数分解をすることで上手く変形することができます。

$$x^2-x-6=0$$

$$(x-3)(x+2)=0$$

$$x-3=0 もしくは　x+2=0$$

$$x=3,   -2$$

(5)の解説！解の公式を使った解き方！

上で紹介した解き方では、どうしても解けない…

そういうときには解の公式を使って解いていきます。

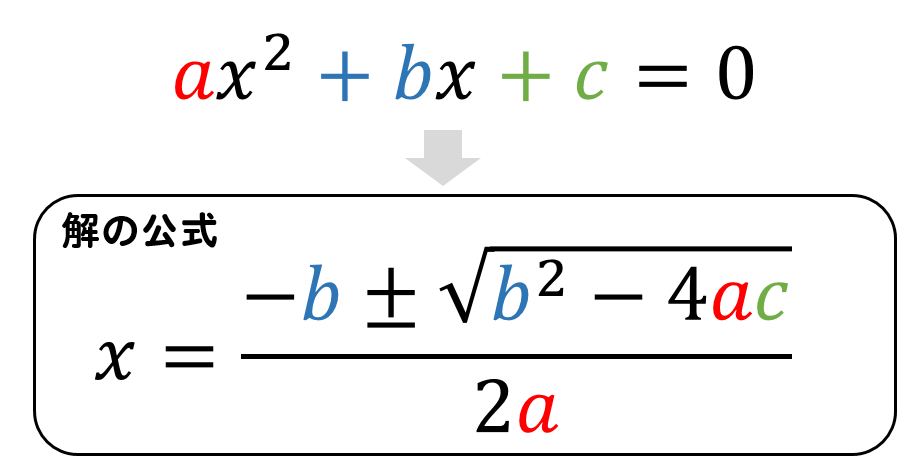
解の公式の使い方については、こちらの記事で解説しています。

＞＞＞【二次方程式】解の公式を利用した解き方を解説！

（5）の解説！

式を見て、解の公式に当てはめる$a, b, c$の値をそれぞれ読み取ります。

すると式から

$$a=5,   b=-1,   c=-2$$

ということが分かりますね。

それぞれの値を解の公式に当てはめていきましょう。

$$x=\frac{-(-1)\pm \sqrt{(-1)^2-4\times 5\times (-2)}}{2\times 5}$$

$$=\frac{1\pm \sqrt{1+40}}{10}$$

$$=\frac{1\pm \sqrt{41}}{10}$$

それでは、二次方程式の解き方が分かったところで入試問題に挑戦して理解を深めていきましょう！

入試問題に挑戦！

まとめ

お疲れ様でした！

二次方程式の解き方はバッチリになりましたか？

二次方程式は解き方がたくさんあるので、ちょっと難しく感じる方もいるかもしれません。

苦手な方は、とにかく演習あるのみです！

問題を眺めているだけでは、解き方は身につきません。

たくさんの問題演習をこなすことで、式を見ただけで解き方が浮かんでくるようになってきますよ(^^)

手を動かすのみ！

ファイトだー(/・ω・)/