今回は中3で学習する
『\(y\)は\(x\)の2乗に比例する\(y=ax^2\)』
の利用問題。
制動距離についての問題を解説していきます！
制動距離？
なんか難しそうな言葉だな…
と思いがちですが
解き方は非常に基本通りな問題です。
１度解説を見ておけば
理解できるはずなので
がんばっていきましょう！
今回の内容はこちらの動画でも解説しています(/・ω・)/
Contents
制動距離とは
車は急には止まれない！
ですよね。
「あ！危ない！！」
と思って、急ブレーキをかけても
車が完全に停止するまでに
車は少し進んでしまいます。
そして
制動距離とは、その少し進んでしまう距離のことをいいます。
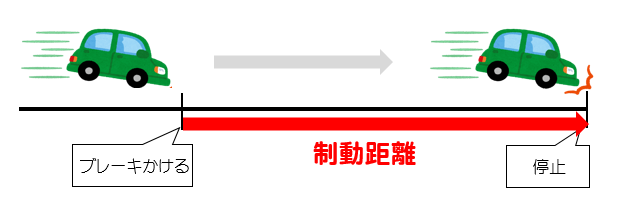
制動距離とは
ブレーキをかけ始めてから完全に停止するまでに進んでしまう距離のこと
をいいます。
そして、この制動距離は
速さの２乗に比例するという特徴があるんですね。
だから、今回の単元で利用問題として扱われるわけです。
制動距離が速さの２乗に比例するというのは
速さが２倍になれば
制動距離は４倍！
速さが３倍になれば
制動距離は９倍に増える！ということです。
ちょっとスピードを上げただけで
こんなにも制動距離は増えちゃうんですね。
ゆっくり走らないと危ないなーって思います。
制動距離の問題を解説
それでは、制動距離について
どのように問題が出題されるのか見ていきましょう。
問題
走っている自動車が ブレーキをかけ始めてから停止するまでに進む距離を制動距離という。この制動距離は自動車の時速の2乗に比例する。時速20kmで走っている自動車が、ブレーキをかけてから止まるまでに進む距離が3mであるとき、次の問いに答えなさい。
（1）時速\(x\)kmのときの制動距離を\(y\)mとして、\(y\)を\(x\)の式で表しなさい。
（2）時速40kmのときの制動距離を求めなさい。
（3）制動距離を27m以下にするには、時速何km以下にすればよいか求めなさい。
（1）の解説！
（1）時速\(x\)kmのときの制動距離を\(y\)mとして、\(y\)を\(x\)の式で表しなさい。
それでは、（1）から解説してきます。
\(x\)と\(y\)の関係式を作る問題ですが
問題文に
『この制動距離は自動車の時速の2乗に比例する。』
とあるように
式は\(y=ax^2\)の形になるということがわかります。
速さを\(x\)、距離を\(y\)としているので
『時速20kmで走っている自動車が、ブレーキをかけてから止まるまでに進む距離が3m』
ここの部分から
\(x=20\)のとき、\(y=3\)になる。
ということが読み取れます。
それぞれの数を
\(y=ax^2\)の式に代入してやると
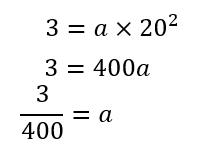
このように\(a\)の値を求めることができました。
よって、答えは
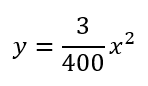
となります。
問題文から\(x\)の値と\(y\)の値をそれぞれ読み取れば
あとは\(y=ax^2\)の式に代入していけばOKですね。
（2）の解説！
（2）時速40kmのときの制動距離を求めなさい。
（2）以降は先ほど作った
\(y＝\frac{3}{400}x^2\)の式を使って計算していきます。
問題文にある
『時速40kmのときの制動距離は？』
というのは
\(x=40\)のとき、\(y\)の値は？
と聞いているのと同じことなので
先ほどの式に\(x=40\)を代入して\(y\)の値を求めてやります。
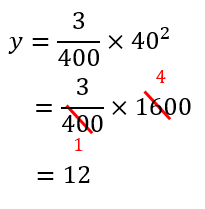
よって、答えは12mとなります。
（1）で式を完成させてしまえば
あとは式の中に数を代入してやるだけですね。
（3）の解説！
（3）制動距離を27m以下にするには、時速何km以下にすればよいか求めなさい。
制動距離を27m以下にするためには
制動距離が27mになるときの速度を求めて
その速度よりも遅くなれば良いと考えます。
つまり、
\(y=27\)になるとき、\(x\)の値は？
ということを求めていけば答えが出ます。
それでは
\(y＝\frac{3}{400}x^2\)の式に\(y=27\)を代入して\(x\)の値を求めましょう。
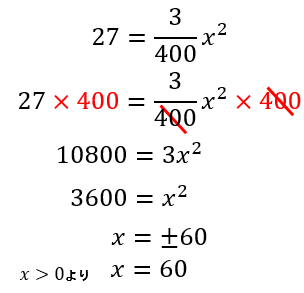
このように、答えは時速60km以下にすれば良いということがわかりました。
最後の問題も式の中に数を代入すれば良いだけでしたね！
練習問題で理解を深めよう！
問題
走っている自動車が ブレーキをかけ始めてから停止するまでに進む距離を制動距離という。この制動距離は自動車の時速の2乗に比例する。時速40kmで走っている自動車が、ブレーキをかけてから止まるまでに進む距離が10mであるとき、次の問いに答えなさい。
（1）時速\(x\)kmのときの制動距離を\(y\)mとして、\(y\)を\(x\)の式で表しなさい。
（2）時速120kmのときの制動距離を求めなさい。
（3）制動距離を40m以下にするには、時速何km以下にすればよいか求めなさい。
（1）時速\(x\)kmのときの制動距離を\(y\)mとして、\(y\)を\(x\)の式で表しなさい。
\(x=40\)のとき、\(y=10\)になるので
\(y＝ax^2\)の式に代入してやると
よって、式は
となります。
（2）時速120kmのときの制動距離を求めなさい。
\(x=120\)のとき、\(y\)の値を求めなさい。
と同じ意味なので
（1）の式に\(x=120\)を代入します。
すると、答えは90mです。
120を2乗するのは大変なので
掛ける前に約分してやると楽に計算できますね。
（3）制動距離を40m以下にするには、時速何km以下にすればよいか求めなさい。
\(y=40\)のとき、\(x\)の値を求めなさい。
と同じ意味なので
（1）で求めた式に\(y=40\)を代入します。
よって、答えは時速80km以下にすれば良いと分かりましたね！
制動距離の問題 まとめ
制動距離とは
ブレーキをかけ始めてから完全に停止するまでに進んでしまう距離のことでしたね。
制動距離のことを知らなくても
問題を解けることは解けるんだけど
ちゃんと理解しておくとイメージがしやすいからね。
そして
速さと制動距離は2乗に比例する関係があったので
問題文から\(x\)と\(y\)の値を読み取れれば
\(y＝ax^2\)に代入していくことで式を求めることができます。
式が完成してしまえば
あとは\(x\)に代入して\(y\)の値を求める。
\(y\)に代入して\(x\)の値を求める。
ということをしていけば解くことができます。
やっていることは
すっごくシンプルで基本的なことばかりなので
制動距離の問題は必ず解けるようにしておいてください。
これで試験の得点アップ！
ファイトだーーーー！
制動距離の利用問題を解説！←今回の記事
数学の成績が落ちてきた…と焦っていませんか？
数スタのメルマガ講座（中学生）では、
以下の内容を無料でお届けします！
① 基礎力アップ！点をあげるための演習問題
② 文章題、図形、関数のニガテをなくすための特別講義
③ テストで得点アップさせるための限定動画
④ オリジナル教材の配布など、様々な企画を実施！
今なら登録特典として、「高校入試で使える公式集」をプレゼントしています！
数スタのメルマガ講座を受講して、一緒に合格を勝ち取りましょう！
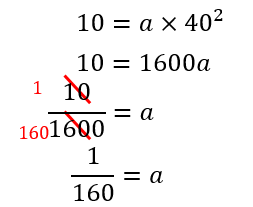
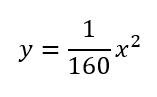
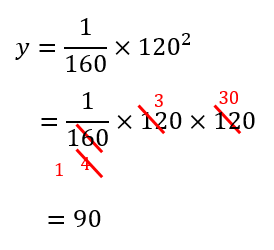
コメントを残す