分散を求めるためには2つの公式がありましたね。
$$s^2=\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2\}$$
$$s^2=\overline{x^2}-(\bar{x})^2$$
今回の記事では
$$s^2=\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2\}$$
こちらの分散公式を式変形して
$$s^2=\overline{x^2}-(\bar{x})^2$$
こちらの公式を導く方法について解説していきます。
数式が長くなり、式が見切れる場合にはヨコにスライドしていただけると式の続きが見れます。
分散公式の式変形
まずはカッコの二乗になっている部分を展開していきます。
展開はそれぞれ
$$(x_1-\bar{x})^2=x_1^2-2x_1\bar{x}+(\bar{x})^2$$
このようになることをおさえておきましょう。
すると
$$s^2=\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2\}$$
$$=\frac{1}{n}\{x_1^2-2x_1\bar{x}+(\bar{x})^2+…+x_n^2-2x_n\bar{x}+(\bar{x})^2\}$$
ここまで展開することができたら

同じ色をつけた部分をグループとしてまとめていきます。
$$=\frac{1}{n}\{(x_1^2+x_2^2+…+x_n^2)-2\bar{x}(x_1+x_2+…+x_n)+n(\bar{x})^2\}$$
次に、\(\displaystyle{\frac{1}{n}}\)をそれぞれのグループに分配法則で掛けていきます。
$$=\frac{1}{n}(x_1^2+x_2^2+…+x_n^2)-\frac{2}{n}\bar{x}(x_1+x_2+…+x_n)+\frac{n}{n}(\bar{x})^2$$
ここで
$$\bar{x}=\frac{x_1+x_2+…+x_n}{n}$$
$$\overline{x^2}=\frac{x_1^2+x_2^2+…+x_n^2}{n}$$
であることを使って、式を変形させます。
$$=\overline{x^2}-2\bar{x}\cdot \bar{x}+(\bar{x})^2$$
$$=\overline{x^2}-2(\bar{x})^2+(\bar{x})^2$$
$$=\overline{x^2}-(\bar{x})^2$$
よって
$$s^2=\overline{x^2}-(\bar{x})^2$$
であることが導けました。
式変形の過程をまとめておきましょう。
$$s^2=\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2\}$$
$$=\frac{1}{n}\{x_1^2-2x_1\bar{x}+(\bar{x})^2+…+x_n^2-2x_n\bar{x}+(\bar{x})^2\}$$
$$=\frac{1}{n}\{(x_1^2+x_2^2+…+x_n^2)-2\bar{x}(x_1+x_2+…+x_n)+n(\bar{x})^2\}$$
$$=\frac{1}{n}(x_1^2+x_2^2+…+x_n^2)-\frac{2}{n}\bar{x}(x_1+x_2+…+x_n)+\frac{n}{n}(\bar{x})^2$$
$$=\overline{x^2}-2\bar{x}\cdot \bar{x}+(\bar{x})^2$$
$$=\overline{x^2}-2(\bar{x})^2+(\bar{x})^2$$
$$=\overline{x^2}-(\bar{x})^2$$
シグマを使ってスマートに式変形
次はシグマを使ってスマートに式変形するパターンをご紹介。
分散の公式はシグマを使って表すと以下のようになります。
$$s^2=\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2\}$$
$$=\frac{1}{n}\sum_{ k= 1 }^{ n }( x_k-\bar{x})^2$$
これを利用して式変形をやってみましょう。
まずは二乗の展開をします。
$$s^2=\frac{1}{n}\sum_{ k= 1 }^{ n }( x_k-\bar{x})^2$$
$$=\frac{1}{n}\sum_{ k= 1 }^{ n }( x_k^2-2x_k\bar{x}+(\bar{x})^2)$$
ここからシグマを分配して分けていきます。
$$=\frac{1}{n}\sum_{ k= 1 }^{ n } {x_k^2}-\frac{1}{n}\sum_{ k= 1 }^{ n }{2x_k\bar{x}}+\frac{1}{n}\sum_{ k= 1 }^{ n }{(\bar{x})^2}$$
そして、\(k\)と関係ない値はシグマの係数として前に出してやります。
$$=\frac{1}{n}\sum_{ k= 1 }^{ n } {x_k^2}-\frac{2\bar{x}}{n}\sum_{ k= 1 }^{ n }{x_k}+\frac{(\bar{x})^2}{n}\sum_{ k= 1 }^{ n }{1}$$
ここで
$$\bar{x}=\frac{x_1+x_2+…+x_n}{n}=\frac{1}{n}\sum_{ k= 1 }^{ n }{x_k}$$
$$\overline{x^2}=\frac{x_1^2+x_2^2+…+x_n^2}{n}=\frac{1}{n}\sum_{ k= 1 }^{ n }{x_k^2}$$
であることを利用して式変形します。
$$=\overline{x^2}-2\bar{x}\cdot \bar{x}+(\bar{x})^2$$
$$=\overline{x^2}-2(\bar{x})^2+(\bar{x})^2$$
$$=\overline{x^2}-(\bar{x})^2$$
よって
$$s^2=\overline{x^2}-(\bar{x})^2$$
であることが導けました。
それでは、シグマを使って式変形する場合をまとめておきましょう。
$$s^2=\frac{1}{n}\sum_{ k= 1 }^{ n }( x_k-\bar{x})^2$$
$$=\frac{1}{n}\sum_{ k= 1 }^{ n }( x_k^2-2x_k\bar{x}+(\bar{x})^2)$$
$$=\frac{1}{n}\sum_{ k= 1 }^{ n } {x_k^2}-\frac{1}{n}\sum_{ k= 1 }^{ n }{2x_k\bar{x}}+\frac{1}{n}\sum_{ k= 1 }^{ n }{(\bar{x})^2}$$
$$=\frac{1}{n}\sum_{ k= 1 }^{ n } {x_k^2}-\frac{2\bar{x}}{n}\sum_{ k= 1 }^{ n }{x_k}+\frac{(\bar{x})^2}{n}\sum_{ k= 1 }^{ n }{1}$$
$$=\overline{x^2}-2\bar{x}\cdot \bar{x}+(\bar{x})^2$$
$$=\overline{x^2}-2(\bar{x})^2+(\bar{x})^2$$
$$=\overline{x^2}-(\bar{x})^2$$
まとめ
シグマを使って式変形をやっていく方がシンプルで見やすいね。
だけど、シグマみたいな数式が苦手だ…
という方は上で紹介したように1つずつ書き出して、まとめていく方が分かりやすかったかもしれませんね。
お好きな方でご理解くださいませ(^^)
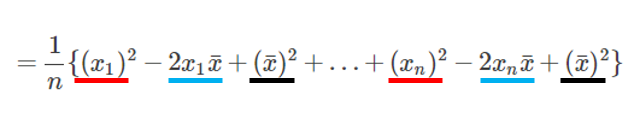
















理解できました!ありがとうございます!!