今回は数学Ⅱで学習する対数関数の単元から
『\(\log\)の大小比較』
について解説していくよ!
対数の大小比較は変形が複雑なモノや
どうやって考えればよいのか…難しい問題も多いです。
今回は様々なパターンの大小比較について解説つけていくので、しっかりと理解を深めていこう!
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
log大小比較の基本的な考え方
まずは、\(\log\)の用語について確認!

\(\log\)のすぐ右についている小さな数は底(てい)
そして、その右についている大きな数は真数(しんすう)といいましたね。
\(\log\)の大小関係を比較するときに、底と真数の関係というのがすごく大切になってきます。
底が1よりも大きい数のとき

\(\log\)の大小関係は、真数の大小関係と等しくなります。
つまり、真数が大きい方が\(\log\)自体も大きいってこと!
そして、底が0から1までの数であるとき
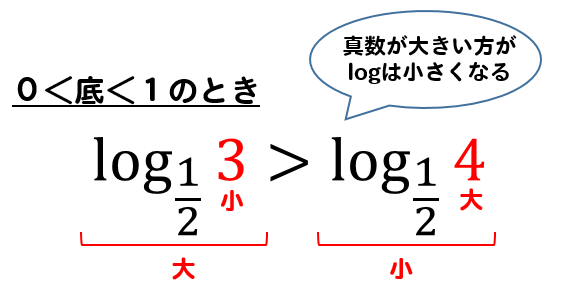
\(\log\)の大小関係は、真数の大小関係と逆になってしまいます。
つまり、真数が大きい方が\(\log\)自体は小さくなるってこと!
このように\(\log\)の大小比較をするときには
それぞれの底が1より大きいか小さいか
そして、真数はどちらが大きいか
この2点を意識して見比べてみると正解を導くことができます。
それでは、簡単な例題を見てみましょう。
次の2つの大小を比べよ。
$$\log_{2}5, \log_{2}6$$
まずは底に注目!
底は2だから1よりも大きいですね。
だから、真数の大小関係がそのまま\(\log\)の大小関係と等しくなります。
真数は\(5<6\)なので\(\log\)の大小もそのままで
$$\log_{2}5<\log_{2}6$$
となります。
次の2つの大小を比べよ。
$$\log_{0.5}5, \log_{0.5}6$$
底は0.5だから、1よりも小さくなっています。
よって、真数の大小関係と\(\log\)の大小関係は逆になります。
真数は\(5<6\)だから、\(\log\)は逆になり
$$\log_{0.5}5>\log_{0.5}6$$
となります。
log大小比較の問題解説!
それでは、\(\log\)の大小比較問題の解き方を見ていきましょう。
\(\log\)の大小比較のポイントは
底を揃えて、真数を比べる!
ということです。
対数どうしに揃える
次の2つの数の大小を比べよ。
$$2, \log_{2}3$$
\(2\)と\( \log_{2}3\)
形が違うので大小を比較するのが難しいですね。
だから、\(2\)を底2とした\(\log\)の形に変形してやりましょう。
$$2=\log_{2}2^2=\log_{2}4$$
そうすると、\(\log_{2}4\)と\(\log_{2}3\)を比較すれば良いということになります。
底は2で、1よりも大きいですね。
だから、真数の大小関係がそのまま\(\log\)の大小関係と等しくなります。
よって
$$\log_{2}4> \log_{2}3$$
となるので
答え
$$2>\log_{2}3$$
両方とも同じ底を持つ\(\log\)の形に揃えてやることで大小比較がしやすくなります。
対数の底を揃える
次の2つの数の大小を比べよ。
$$\log_{3}5, \log_{9}16$$
底が3と9であり、揃っていません。
このままでは大小比較ができないので、まずは底を揃えていきます。
\(\log_{9}16\)の対数を底3となるよう変形します。
$$\log_{9}16=\frac{\log_{3}16}{\log_{3}9}$$
$$=\frac{\log_{3}4^2}{2}$$
$$=\frac{2\log_{3}4}{2}$$
$$=\log_{3}4$$
つまり、\(\log_{3}5\)と\(\log_{3}4\)の大小を比較すればよいということになります。
底3は1より大きいので、真数の大小関係がそのまま\(\log\)の大小関係になります。
よって
$$\log_{3}5>\log_{3}4$$
答え
$$\log_{3}5>\log_{9}16$$
底が揃っていなければ、揃える!
真数が揃っている問題
次の3つの数の大小を比べよ
$$\log_{0.5}4, \log_{2}4, \log_{3}4$$
今回の問題では真数部分がすべて揃っていますね。
こういう場合には、底を真数である4に揃えてみると比較しやすくなります。
$$\log_{0.5}4=\frac{\log_{4}4}{\log_{4}0.5}$$
$$=\frac{1}{\log_{4}0.5}$$
\(\log_{4}0.5<\log_{4}1=0\)だから
$$\frac{1}{\log_{4}0.5}<0$$
ということがわかりますね。
次に
$$\log_{2}4=\frac{\log_{4}4}{\log_{4}2}$$
$$=\frac{1}{\log_{4}2}$$
$$\log_{3}4=\frac{\log_{4}4}{\log_{4}3}$$
$$=\frac{1}{\log_{4}3}$$
分母にある\(\log\)の大小関係を比較すると
$$0=\log_{4}1<\log_{4}2<\log_{4}3$$
これらの数を逆数にすると、大小関係はひっくり返り
$$\frac{1}{\log_{4}2}>\frac{1}{\log_{4}3}>0$$
となります。
よって、以上のことをまとめると
答え
$$\log_{0.5}4<\log_{3}4<\log_{2}4$$
【応用】分数と比較する問題
次の2つの数の大小を比べよ。
$$\log_{10}2, \frac{3}{10}$$
\(\displaystyle{\frac{3}{10}}\)を対数の形に変形しましょう。
$$\frac{3}{10}=\log_{10}10^\frac{3}{10}$$
ともに\(\log\)の形に変形できたので

真数である2と\(\displaystyle{10^\frac{3}{10}}\)の大小を考えればよいということになります。
しかし…
\(\displaystyle{10^\frac{3}{10}}\)ってなに!?
という感じで困ってしまいます。
なので、両方の数を10乗してから大小関係を比較します。
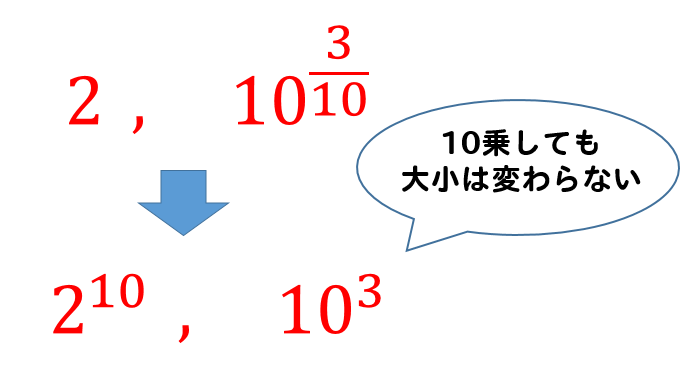
両方とも正の数だから、10乗したところで大小関係は変化しないよね!
$$2^{10}=1024$$
$$10^3=1000$$
よって、\(2^{10}>10^3\)であり
$$2>10^\frac{3}{10}$$
ということが分かりました。
以上のことより
答え
$$\log_{10}2>\frac{3}{10}$$
まとめ
お疲れ様でした!
\(\log\)の大小関係を比べるときには
底を揃えて、真数を比べるというのが基本線になります。
しかし、それだけでは解けない問題も存在します。
そういうときにどういった考え方を用いれば良いのか
そういった引き出しをたくさん持っておくことが大切ですね。
今回解説したような問題は、テストや模試でも良く出題される考え方なのでしっかりとマスターしておきましょう。
ファイトだ(/・ω・)/
















コメントを残す