こんにちは!数スタの小田です。
今回は中3で学習する展開・因数分解の単元から「計算の工夫」について解説していきます。この単元の総まとめ的な内容になっているので、ここができるようになるとテストでもグッと点が伸びてきます^^
なので、気合を入れてがんばっていきましょう!
取り上げる問題はこちらです。
【問題①】次の式を工夫して計算しなさい。
(1)\(25^2-15^2\)
(2)\(57\times 63\)
【問題②】次の式を工夫して計算しなさい。
(1)\(101^2\)
(2)\(98^2\)
【問題③】次の式の値を求めなさい。
(1)\(x=12\)のとき、\((x+7)(x-1)-(x+9)(x-4)\)
(2)\(x=2.7, y=2.3\)のとき、\(x^2-y^2\)

計算の工夫のやり方①
【問題①】次の式を工夫して計算しなさい。
(1)\(25^2-15^2\)
(2)\(57\times 63\)
これらの計算をするときに活用するのがこちら!

(1)の式を乗法公式③に当てはめると次のように計算できます。

とても簡単ですね!暗算で計算することもできます^^
「2乗ひく2乗」の式であれば因数分解する!
これを覚えておきましょう。
続いて(2)ですが、これはちょっと工夫が必要!

57と63に対して、共通する基準値を決めます。今回であれば60が基準にとることで、それぞれの数を
$$57 ⇒ 60-3$$
$$63 ⇒ 60+3$$
このように60と3で表すことができます。
これにより乗法公式③が使えるようになるので、サクッと計算を進めていくことができます。
とはいえ…\(3600-9\)という計算をミスっちゃう人が多いので注意してくださいね(._.)
計算の工夫のやり方②
【問題②】次の式を工夫して計算しなさい。
(1)\(101^2\)
(2)\(98^2\)
\((大きい数)^2\) という式が出てきたときに使うのがコレ!

それぞれ次のように式を変形して計算していきましょう!
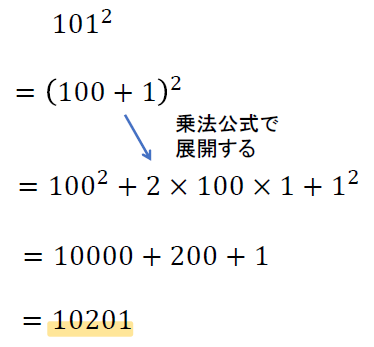

それぞれ\((キリのいい数+〇)(キリのいい数-△)\)といった式に変形することで、乗法公式を使っても暗算でラクに計算を進めることができますね!
この計算は慣れるまでミスが起こりやすいので、何度も練習しておきましょう(‘ω’)ノ
特に\(100^2\)の計算で、0の数を間違えてしまう人が多い…!
\(100^2\)では、100×100で00が2個なので、答えには「10000」と0が4個くっつく形になります。0の数を間違えないように注意してくださいね。
計算の工夫のやり方③
【問題③】次の式の値を求めなさい。
(1)\(x=12\)のとき、\((x+7)(x-1)-(x+9)(x-4)\)
(2)\(x=2.7, y=2.3\)のとき、\(x^2-y^2\)
そのまま代入しようとすると計算が大変になっちゃいますね…
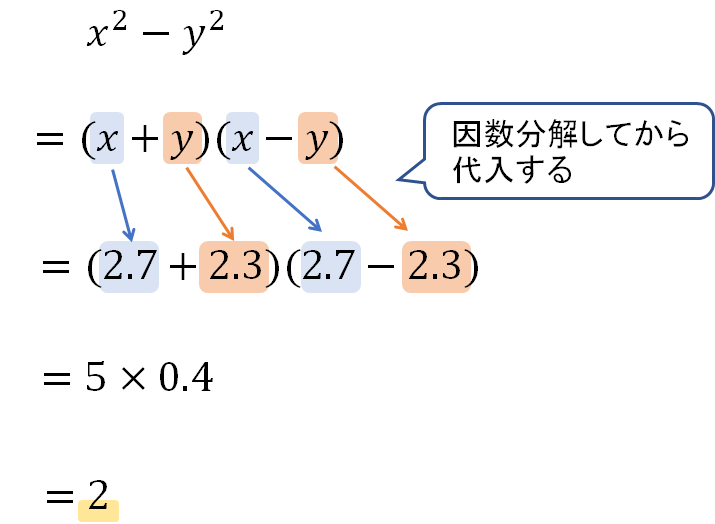
なので、(1)では展開をしてから代入、(2)では因数分解してから代入。
これで計算をラクにしながら進めていきましょう。

【特典課題】動画付の演習プリントを用意しました!
お疲れ様でした!これで計算の工夫はバッチリですね^^
あとは学校のワークなどを活用して、いろんな計算を練習してテストに備えておきましょう!
今回の学習内容をご自宅でお子さんにも取り組ませたいとお考えの保護者さんへ!
先生がそばにいなくても1人でスラスラ最後までやり切れる!
そんな動画講義&演習プリントを用意しました。
冒頭でもお伝えしたように、今回の内容は展開・因数分解の単元において、総まとめ的なものとなっています。そのため、テストでも配点が高く出題されることが多く、しっかりと対策しておくことで得点UPが期待できます!
というわけで、記事を読んで終わり~ではなく、この追加講義&プリントを活用して細かいポイントまで完璧に習得してください^^
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^

















98の二乗の問題の答えが間違っています。正しくは9604です。
ミスってました…お恥ずかしい。
ご指摘ありがとうございました!
いいと思う