今回は中2で学習する確率の単元から
「座標と確率の融合問題」
について解説していきます。
取り上げる問題はこちら！
【問題】
大小2つのサイコロを同時に投げる。
大きいサイコロの出た目の数を\(a\)、小さいサイコロの出た目の数を\(b\)として、座標平面上に点\(P(a.b),Q(4.5),R(4.3)\)を取るとき、次の確率を求めなさい。
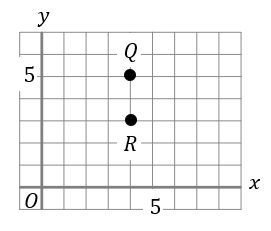
（1）点\(P\)が直線\(y＝x\)上にある確率
（2）\(△PQR\)の面積が2になる確率
（3）\(△PQR\)が二等辺三角形になる確率
ちょっと発展的な問題になりますが、入試レベルを目指す方には必ず解いてもらいたい内容です。
気合い入れていきましょう(‘ω’)ノ
（1）直線上にある確率
まずは、\(y=x\)の直線をグラフに書き込んでみましょう！
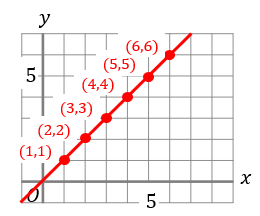
そのグラフ上の座標を見ながら、さいころの目の数（1～6）を使って表されるものをチェックしていきます。
すると図のように\((1,1)(2,2)(3,3)(4,4)(5,5)(6,6)\)の6通りであることがわかりますね！
さいころを2個投げる場合は、全部で36通りの目の出方があるので、確率は\(\frac{6}{36}=\frac{1}{6}\)となります。
答え
（1）\(\frac{1}{6}\)
（2）面積が2になる確率
QR（長さ2）を底辺として考えると、面積を2にするためには、
$$\begin{eqnarray}△PQR&=&QR\times 高さ \times \frac{1}{2} \\[5pt]2&=&2\times 高さ\times \frac{1}{2}\\[5pt]2&=&高さ\end{eqnarray}$$
このように、高さが2になるように点Pをとれば面積も2になることがわかります。
というわけで、QRを底辺としたとき、高さが2になるためには
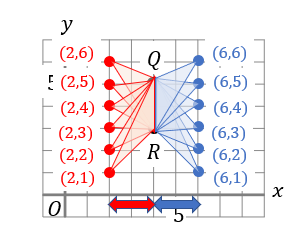
このように左側に点Pをとった場合
\((2,1)(2,2)(2,3)(2,4)(2,5)(2,6)\) の6通り。
右側に点Pをとった場合
\((6,1)(6,2)(6,3)(6,4)(6,5)(6,6)\) の6通り。
合計で12通りあることがわかりますね！
よって、確率は\(\frac{12}{36}=\frac{1}{3}\)となります。
答え
（2）\(\frac{1}{3}\)
（3）二等辺三角形になる確率
△PQRが二等辺三角形になるには2辺が等しくなる必要があるのですが、その2辺の選び方には次の2パターンあります。
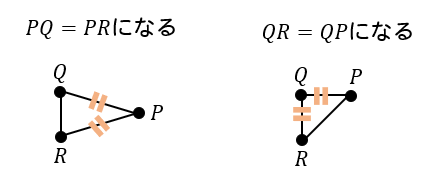
まず、\(PQ=PR\)になる場合を考えると、
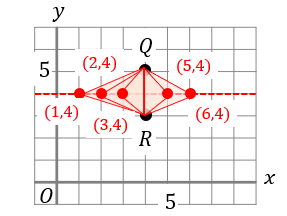
このようにQRの中点のライン上に点Pがくればいいので、全部で5通りになります。
\((4,4)\)のときは、△PQRは三角形がつくれなくなるので除外してくださいね！
次に、\(QR=QP\)のときを考えると、
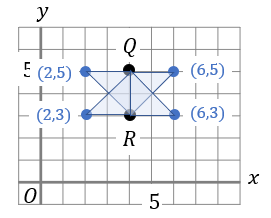
点Q、Rから長さが2になるところに点Pをとればいいので、全部で4通り見つかります。
よって、2つのパターンを合計すると9通りになるので、確率は\(\frac{9}{36}=\frac{1}{4}\)となります。
答え
（3）\(\frac{1}{4}\)
類題で理解を深めよう！
【問題】
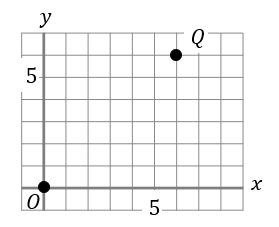
1つのさいころを2回投げ、1回目に出た目の数を\(a\)、2回目に出た目の数を\(b\)とするとき、座標平面上に、点Ｐ\((a,b)\)をとります。点Ｑの座標を\((6,6)\)とするとき、\(△POQ\) が二等辺三角形になる確率を求めなさい。
答え
$$\frac{1}{9}$$
OQの中点\((3,3)\)を通る垂直な直線上にある座標をチェックしていきましょう。
今回の問題では\(OP=OQ\)となるパターンは作れないので考えなくてOKですね！
コメントを残す