【くじ引きの確率】くじを戻す、戻さないそれぞれの問題を解説！

今回は、中学・高校数学で学習するレベルの確率から

『くじ引きの確率』

について解説していきます。

取り上げるの次の問題

くじを元に戻さないパターン

（1）Aが当たる確率

これは超簡単だね！

一番最初にくじを引くAさん

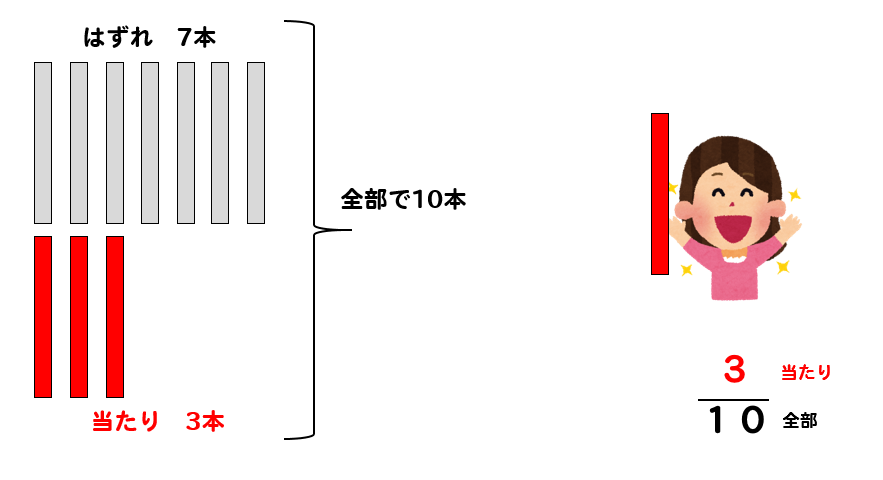
全体のくじが10本あり、その中に当たりが3本あるのだから確率は

$$\LARGE{\frac{3}{10}}$$

となります。

（2）A、Bともに当たる確率

Aが当たり、続いてBも当たる確率を考えてみましょう。

まず最初にくじを引くAが当たる確率は、（1）で求めたように\(\displaystyle{\frac{3}{10}}\)となります。

そして、次にBがくじを引くのですが、そのとき残っているくじは…

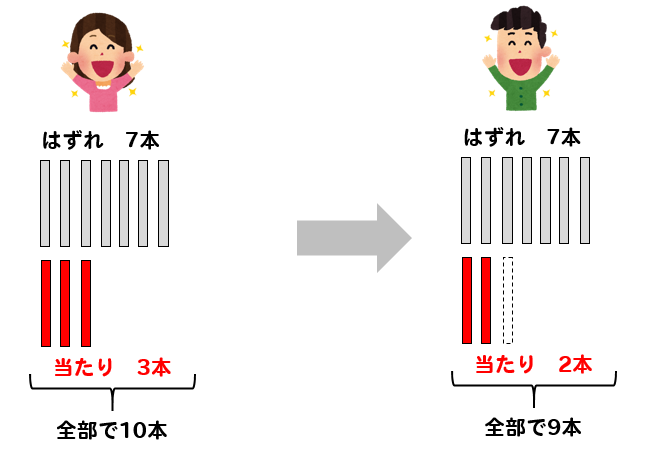
はずれが7本、当たりが2本の計9本になっています。

つまり、1回目にAが当たった場合に、2回目にBが当たりを引く確率は\(\displaystyle{\frac{2}{9}}\)となります。

よって、確率は

このようになります。

（3）Bが当たる確率

2番目にくじを引くBさんが当たるということは、次のパターンが考えられます。

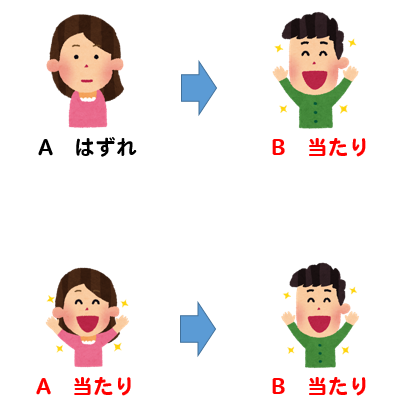
よって、Bが当たる確率を求めたいとき

Aはずれ　⇒　B当たり

A当たり　⇒　B当たり

それぞれのパターンの確率を求め、その確率を合計することで求めていきます。

まず、AがはずれてからBが当たる確率

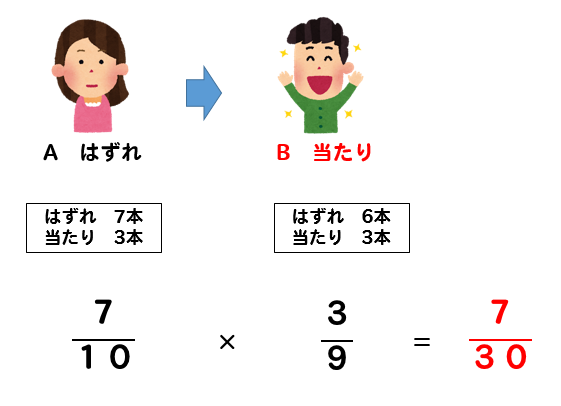
次は、Aが当たってBも当たる確率

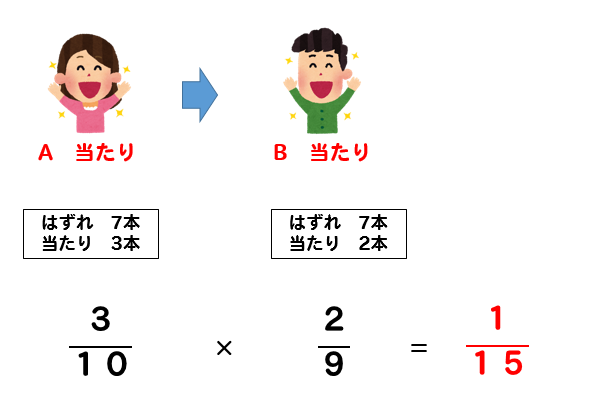
以上より、Bが当たる確率は

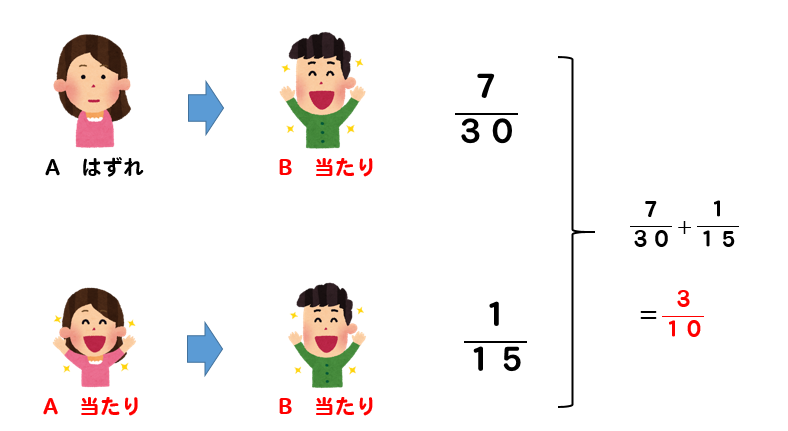
このようになります。

くじを元に戻さないパターンでは、2回目にくじを引くとき、はずれと当たりがそれぞれ何本ずつ残っているのかを考えることが大事ですね！

更に、注目してほしいのは

1回目にくじを引いて当たりを引く確率（1）

2回目にくじを引いて当たりを引く確率（3）

がそれぞれ\(\displaystyle{\frac{3}{10}}\)となっており、確率が等しいことが分かります。

つまり、くじ引きは最初に引いても、後から引いても計算上は当たる確率が一緒ってことだね！

『残り物には福がある』

なんて言ったりしますが、数学的には

どっちも一緒や！

ということです。

くじを元に戻すパターン

（1）Aが当たる確率

1回目にくじを引く人は、くじを元に戻す戻さないは関係ありませんね。

よって、Aが当たる確率は

$$\LARGE{\frac{3}{10}}$$

となります。

（2）A、Bともに当たる確率

引いたくじを元に戻すということだから、1回目にくじを引くAと2回目にくじを引くBは条件が同じになります。

よって、確率は

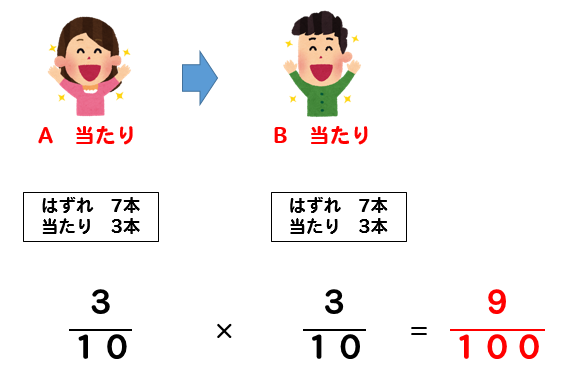
このようになります。

（3）Bが当たる確率

くじを元に戻さない場合でやったように、Bが当たるというのは

この2パターン考えられます。

これらを、くじを戻す場合で考えてみると

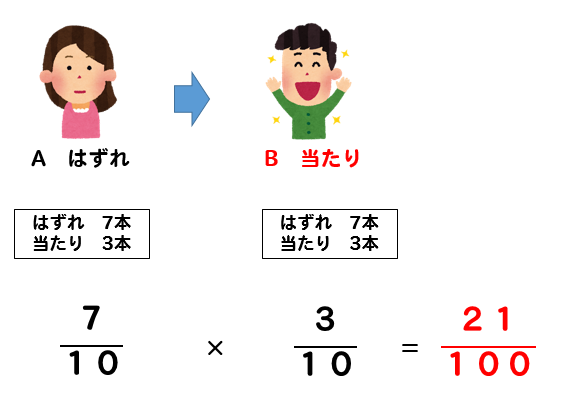
このように求めることができます。

よって、Bが当たる確率は

$$\large{\frac{21}{100}+\frac{9}{100}}$$

$$\large{=\frac{30}{100}}$$

$$\large{=\frac{3}{10}}$$

となります。

結局、AとB

どちらも当たる確率は一緒だな

ってことが分かりますね。

くじを元に戻す場合には、はずれ当たりの本数は変化しません。

なので、何回目であっても当たり、はずれの確率は同じとして考えていくことができますね。

テストに強くなる！確率の点を伸ばす定期対策ドリルをプレゼント！

お疲れ様でした＾＾

これでくじ引きの確率のやり方は理解してもらえたと思います！

ただ、今回のようにさいころだけ、硬貨だけ、玉を取り出すだけ…のようにパターン別に演習をやっていると、頭を使うことなく流れで解けてしまうことが多いです。

実際のテストではどのパターンが出題されるかはランダムであり「表を使って考える？」「樹形図を使って考える？」といったことを問題文から解法を瞬時に判断していかないといけません。

というわけで！

今回は確率のテスト対策として、「問題⇒パッと解き方を判断」という特訓ができるような実戦演習を用意しました。

動画解説もつけているので苦手なお子さんでも1人で取り組めますよ＾＾

確率は他の単元に比べて、難しい公式、計算が出てこないので、数学をニガテにしている方でも点が伸ばしやすいです！なので、今回の課題も活用しながら、早めのテスト対策をしていきましょう(‘ω’)ノ

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

くじ引きの問題では、問題文に書いてある

くじを戻す、戻さない

というワードが非常に大事です。

ここを見落としてしまうと考え方が破綻してしまいます…

見落としがないよう、問題文を細かくチェックするようにしましょう。

そして、くじを元に戻さない場合では

2回目にくじを引く人は、1回目の人が何を引いたのかによって確率が変わってきてしまいます。

状況を考えながら、はずれ当たりくじが何本ずつ残っているのかをしっかりと判断して考えていくようにしましょう！

以上(/・ω・)/