今回は中2数学で学習する確率の単元から「整数を作る確率」について解説していきます。
この問題でのポイントは、しっかりと樹形図をつくることですね!
では、それぞれの問題の解き方を確認していきましょう(‘ω’)ノ
<取り上げる問題>
(整数を作る確率①)
0,1,2,3の数字を1つずつ書いた4枚のカードがある。このカードを2枚並べて2桁の整数をつくる。
(1)2桁の整数は全部で何通りあるか。
(2)できた整数が偶数になる確率を求めなさい。
(整数を作る確率②)
1,2,3,4の数字を1つずつ書いた4枚のカードがある。このカードを2枚並べて2桁の整数をつくる。
(1)できた整数が30以上になる確率を求めなさい。
(2)できた整数が3の倍数になる確率を求めなさい。
(整数を作る確率③)
1,2,3の数字を1つずつ書いた3枚のカードがある。このカードを左から1列に並べて3桁の整数をつくる。
(1)できる整数が230以下になる確率を求めなさい。
(2)できる整数が奇数になる確率を求めなさい。
今回の内容はこちらの動画でも解説しているのでご参考ください^^

整数をつくる確率①
0,1,2,3の数字を1つずつ書いた4枚のカードがある。このカードを2枚並べて2桁の整数をつくる。
(1)2桁の整数は全部で何通りあるか。
(2)できた整数が偶数になる確率を求めなさい。
ひこ樹形図をかいて考えよう!
0は先頭に来ちゃダメなので注意!
0、1、2、3の4枚のカードを2枚並べる樹形図をかきましょう。
2桁の整数にしたいので、先頭に0を置くことができません。
(01 ⇒ 1 になっちゃうから2桁ではなくなる)
その点に注意して樹形図をかくと…

このように全部で9通りあることが分かります!
さらに偶数になっている数は「10、12、20、30、32」の5通りであることがわかるので確率は\(\frac{5}{9}\)となります。
答え
(1)9通り
(2)\(\frac{5}{9}\)
整数をつくる確率②
1,2,3,4の数字を1つずつ書いた4枚のカードがある。このカードを2枚並べて2桁の整数をつくる。
(1)できた整数が30以上になる確率を求めなさい。
(2)できた整数が3の倍数になる確率を求めなさい。
今回の数字には0が含まれていないので、注意する点が少なくてラッキーですね^^
4枚の数を使って樹形図をかくと次のようになります。
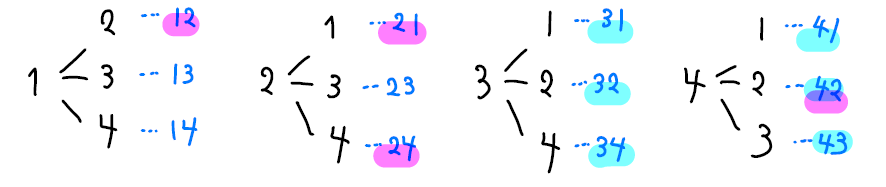
全部で12通りあって、30以上になる整数は「31,32,34,41,42,43」の6通り、3の倍数になる整数は「12,21,24,42」の4通りあることが読み取れます。
3の倍数というのは、3で割り切れるという意味です。
\(12\div3=4\) で割り切れるから12は3の倍数
\(13\div3=4…1\) で割り切れないから13は3の倍数ではない
このように判断していきましょう^^
よって、それぞれの答えは以下の通りです。
答え
(1)12通り
(2)\(\frac{6}{12}=\frac{1}{2}\)
(3)\(\frac{4}{12}=\frac{1}{3}\)
樹形図がしっかりとかければ簡単に答えが出せますね^^
整数を作る確率③
1,2,3の数字を1つずつ書いた3枚のカードがある。このカードを左から1列に並べて3桁の整数をつくる。
(1)できる整数が230以下になる確率を求めなさい。
(2)できる整数が奇数になる確率を求めなさい。
今回は3桁の整数なので樹形図は次のようになります。
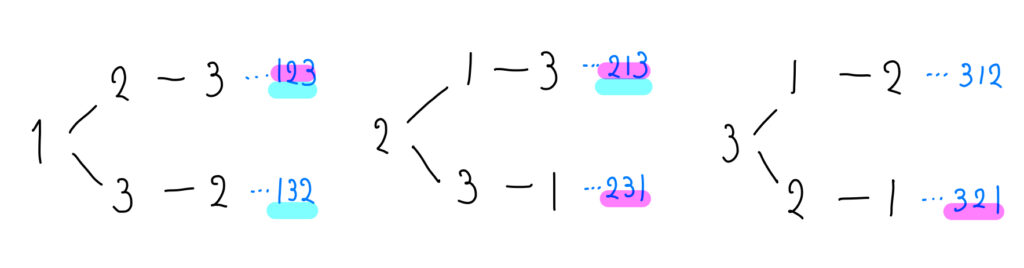
全部で6通りあって、230以下になる整数は「123,132,213」の3通り、奇数になる整数は「123,213,231,321」の4通りあることが読み取れます。
よって、それぞれの答えは以下の通りです。
答え
(1)6通り
(2)\(\frac{3}{6}=\frac{1}{2}\)
(3)\(\frac{4}{6}=\frac{2}{3}\)
ちなみに、奇数か偶数かの判断については一の位をチェックすれば簡単ですね^^


テストに強くなる!確率の点を伸ばす定期対策ドリルをプレゼント!
お疲れ様でした^^
これで整数をつくる確率のやり方は理解してもらえたと思います!
ただ、今回のようにさいころだけ、硬貨だけ、玉を取り出すだけ…のようにパターン別に演習をやっていると、頭を使うことなく流れで解けてしまうことが多いです。
実際のテストではどのパターンが出題されるかはランダムであり「表を使って考える?」「樹形図を使って考える?」といったことを問題文から解法を瞬時に判断していかないといけません。
というわけで!
今回は確率のテスト対策として、「問題⇒パッと解き方を判断」という特訓ができるような実戦演習を用意しました。

動画解説もつけているので苦手なお子さんでも1人で取り組めますよ^^
確率は他の単元に比べて、難しい公式、計算が出てこないので、数学をニガテにしている方でも点が伸ばしやすいです!なので、今回の課題も活用しながら、早めのテスト対策をしていきましょう(‘ω’)ノ
【定期対策ドリル】確率基礎を無料で受け取る!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れ様でした!
整数を作るような問題ではしっかりと樹形図をかくことが大事です。
めんどいかもしれないけど、ちゃんとかこうね(‘◇’)ゞ
整数を作る確率では、
「偶数、奇数」「〇の倍数」「△以上になる」
このような条件が与えられることが多いです。
それぞれの判断の仕方についても覚えておいてくださいね!














コメントを残す