今回は中2で学習する確率の単元の中からさいころの問題を徹底解説していくよ！
さいころの問題は確率の中でもダントツに出題率が高いからしっかりとマスターしておこう！
今回の内容をサクッと理解したい方はこちらの動画がおススメです＾＾
さいころ2個は表を使って考えよう！
さいころの確率問題では
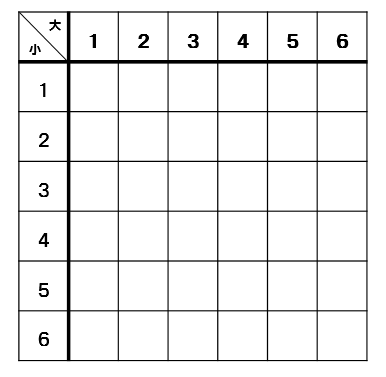
このような6マス×6マスの表を使って考えると、とーっても分かりやすいからおススメです！
この表の見方としては
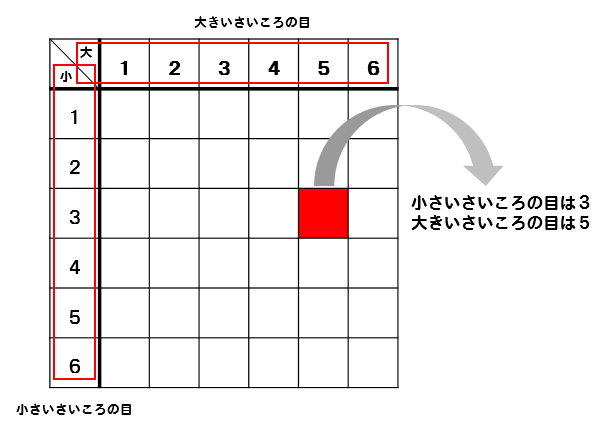
タテとヨコをそれぞれ大きいさいころ、小さいさいころの目だと考えて見ていきます。
それでは、この表を使ってどのように問題を解いていくのかを問題のパターン別に解説していきます。
がんばってマスターしていこう！
同じ目になる確率
まずは、2つのさいころの出た目が同じになる確率から考えてみましょう。
大小2つのさいころを同時に投げるとき、同じ目が出る確率を求めなさい。
それでは、表を使って考えて見ましょう。
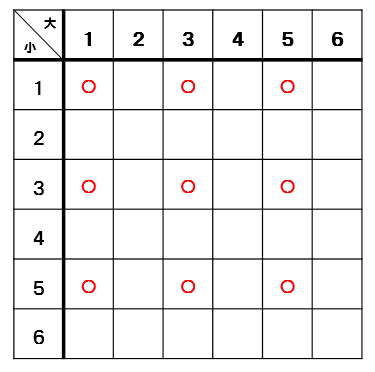
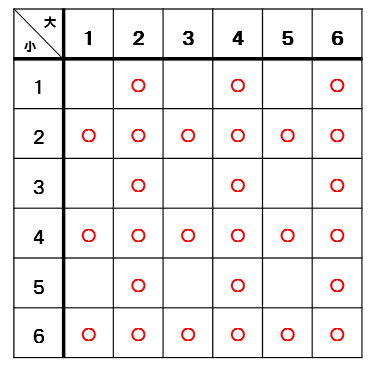
大小が同じ数になっているマスに印をつけると、
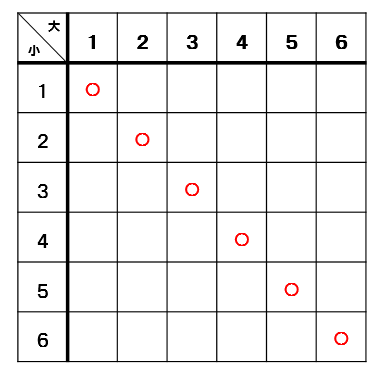
このようになります。
全部で6個の〇がつきました。
36マスある中で6個〇がついたので確率は
$$\frac{6}{36}=\frac{1}{6}$$
となります。
表を使えば、2個のさいころ確率は簡単です！
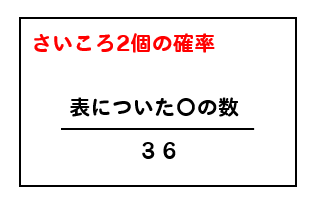
このように考えていけば解けますね！
それでは、演習問題にも挑戦してみましょう。
演習問題で理解を深める！
大小2つのさいころを同時に投げるとき、出た目が両方とも偶数になる確率を求めなさい。
答え
$$\frac{1}{4}$$
大小、それぞれ偶数になっているところに〇をつけると9個ありますね！
よって
$$\frac{9}{36}=\frac{1}{4}$$
大小2つのさいころを同時に投げるとき、出た目が両方とも奇数になる確率を求めなさい。
答え
$$\frac{1}{4}$$
大小、それぞれ奇数になっているところに〇をつけると9個ありますね！
よって
$$\frac{9}{36}=\frac{1}{4}$$
偶数も奇数も同じ確率になることがわかりましたね。
出た目の和を考える確率
次は、さいころの出た目を足した数についての確率を見ていきましょう。
大小2つのさいころを同時に投げるとき、出る目の数の和が5になる確率を求めなさい。
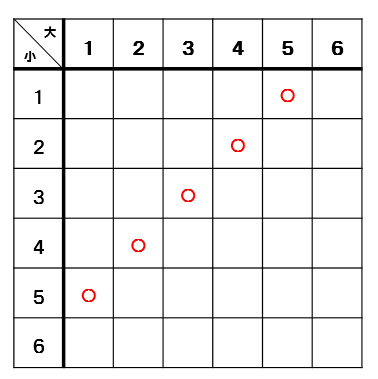
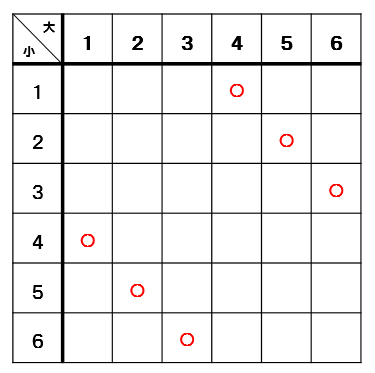
表を見ながら、足して5になるところに〇をつけていきます。
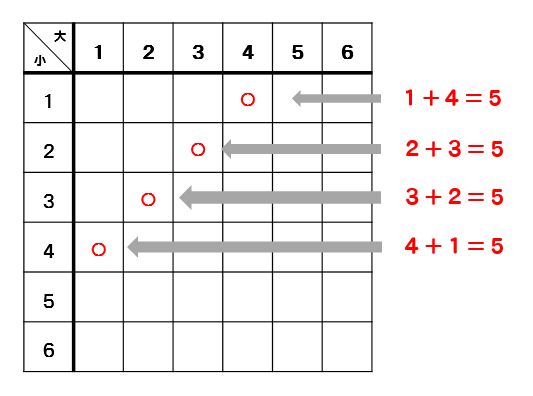
すると、4個の〇がついたので足して5になる確率は
$$\frac{4}{36}=\frac{1}{9}$$
となります。
これも表を使っていけば簡単ですね！
演習問題で理解を深める！
大小2つのさいころを同時に投げるとき、出る目の数の和が6になる確率を求めなさい。
答え
$$\frac{5}{36}$$
足して6になるのは
$$(1,5)(2,4)(3,3)(4,2)(5,1)$$の5個あるので
$$\frac{5}{36}$$
となります。
大小2つのさいころを同時に投げるとき、出る目の数の和が7になる確率を求めなさい。
答え
$$\frac{1}{6}$$
足して7になるのは、\((1,6)(2,5)(3,4)(4,3)(5,2)(6,1)\)の6個あるので
$$\frac{6}{36}=\frac{1}{6}$$
となります。
大小2つのさいころを同時に投げるとき、出る目の数の和が10になる確率を求めなさい。
答え
$$\frac{1}{12}$$
足して10になるのは、\((4,6)(5,5)(6,4)\)の3個あるので
$$\frac{3}{36}=\frac{1}{12}$$
となります。
出た目の積を考える確率
次は、出た目の積。
つまりかけ算した値について考えてみましょう。
大小2つのさいころを投げるとき、出た目の積が12になる確率を求めなさい。
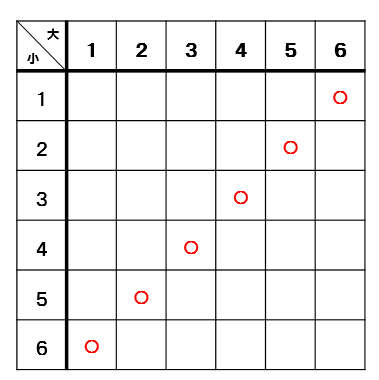
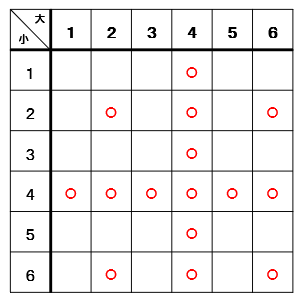
表を見ながら、掛けて12になるところに〇をつけていきます。
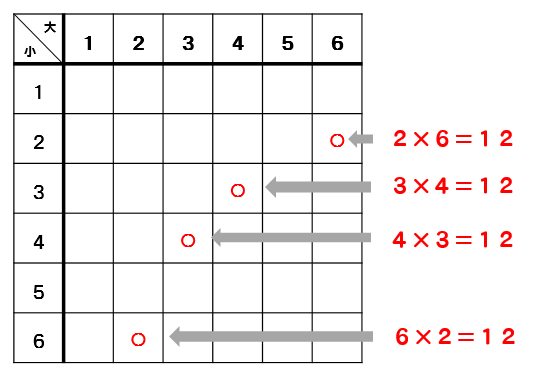
すると、4個の〇がついたので掛けて12になる確率は
$$\frac{4}{36}=\frac{1}{9}$$
となります。
それでは、演習問題で理解を深めていきましょう！
演習問題で理解を深める！
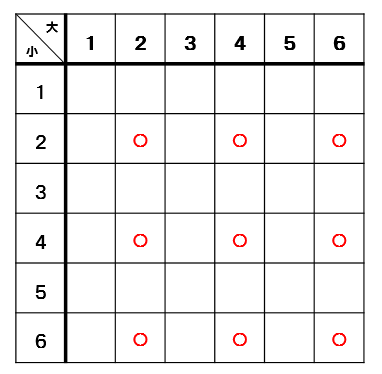
大小2つのさいころを同時に投げるとき、出る目の数の積が偶数になる確率を求めなさい。
答え
$$\frac{3}{4}$$
〇がたくさんあって、目がチカチカしますね。笑
大小どちらかの数が偶数になっていればそれらを掛けた値も偶数になるので、たくさん〇がつきました。
全部で27個あるので
$$\frac{27}{36}=\frac{3}{4}$$
となります。
大小2つのさいころを同時に投げるとき、出る目の数の積が4の倍数になる確率を求めなさい。
答え
$$\frac{5}{12}$$
掛けて4の倍数になるのは、全部で15個ありました。
よって
$$\frac{15}{36}=\frac{5}{12}$$
となります。
出た目の差を考える確率
次は、出た目の差を考えていきます。
差というのは大きい数から小さい数を引いたものを考えるので、\((2,4)\)が出た場合と\((4,2)\)が出た場合は両方とも差は\(4-2=2\)と考えていくからね！
大小2つのさいころを同時に投げるとき、出る目の差が2になる確率を求めなさい。
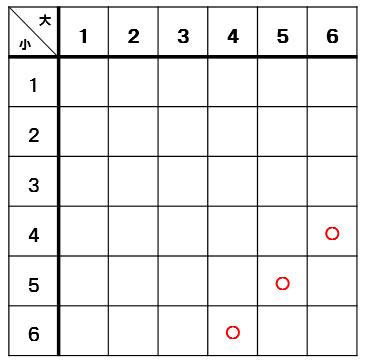
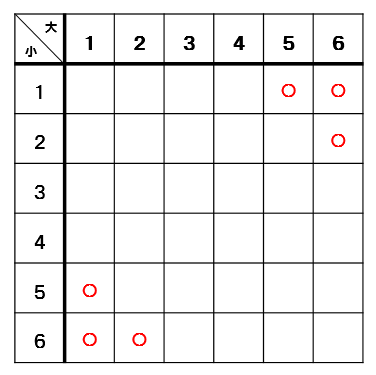
出た目の差が2になるところに〇をつけていくと
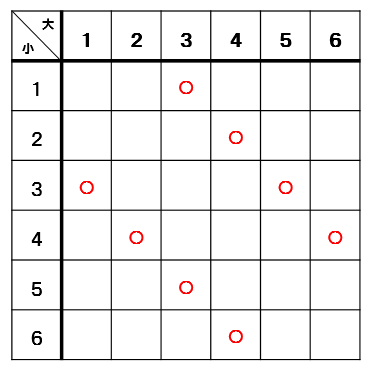
このように〇が8個あるので
$$\frac{8}{36}=\frac{2}{9}$$
となります。
差を考える問題では、負の数は出てこないから気を付けてね！
それでは、演習問題に挑戦してみよう。
演習問題で理解を深める！
大小2つのさいころを同時に投げるとき、出る目の数の差が3になる確率を求めなさい。
答え
$$\frac{1}{6}$$
出た目の差が3になるのは
$$(1,4)(2,5)(3,6)(4,1)(5,2)(6,3)$$
の6個あるので
$$\frac{6}{36}=\frac{1}{6}$$
となります。
大小2つのさいころを同時に投げるとき、出る目の数の差が4以上になる確率を求めなさい。
答え
$$\frac{1}{6}$$
問題文をよく読んでくださいね。
差が4以上になるときの確率なので
差が４、５のときを考える必要があります。
差が4になるのが、\((1,5)(2,6)(5,1)(6,2)\)の4個。
差が5になるのが、\((1,6)(6,1)\)の2個。
よって、差が4以上になるのは6個あります。
つまり確率は
$$\frac{6}{36}=\frac{1}{6}$$
となります。
テストに強くなる！確率の点を伸ばす定期対策ドリルをプレゼント！
お疲れ様でした＾＾
これでさいころの確率のやり方は理解してもらえたと思います！
ただ、今回のようにさいころだけ、硬貨だけ、玉を取り出すだけ…のようにパターン別に演習をやっていると、頭を使うことなく流れで解けてしまうことが多いです。
実際のテストではどのパターンが出題されるかはランダムであり「表を使って考える？」「樹形図を使って考える？」といったことを問題文から解法を瞬時に判断していかないといけません。
というわけで！
今回は確率のテスト対策として、「問題⇒パッと解き方を判断」という特訓ができるような実戦演習を用意しました。
動画解説もつけているので苦手なお子さんでも1人で取り組めますよ＾＾
確率は他の単元に比べて、難しい公式、計算が出てこないので、数学をニガテにしている方でも点が伸ばしやすいです！なので、今回の課題も活用しながら、早めのテスト対策をしていきましょう(‘ω’)ノ
【定期対策ドリル】確率基礎を無料で受け取る！
「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾
（ご登録いただいたメールアドレスに教材を送らせていただきます）
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！
このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾
さいころの確率問題 まとめ
お疲れ様でした！
さいころ2個の問題は表を使って考えることで簡単に解くことができます。
今回紹介した問題はさいころ確率の基本的なものばかりでしたが、発展問題に関しても、表を使って考えれば大丈夫！
基本問題がバッチリになった人は、応用問題にも挑戦してみましょう(^^)
ファイトだー(/・ω・)/
さいころ2個の確率問題をパターン別に解説！←今回の記事
出るの積が４の倍数のときの答えに誤りがあります。
５＊６は４の倍数ではないと思われます。
ご指摘ありがとうございます！
訂正しておきました！
ありがとう
こちらこそありがとう！
勉強がんばって＾＾
とても分かりやすかったです。
ありがとうございます！！